汉罗塔问题

C语言复习——汉罗塔问题

①先理解一下最典型的递归问题：求n的阶乘

{
 int jc(int n);
 int n,y;
 printf("请输入n的值：");
 scanf("%d",&n);
 y=jc(n);
 printf("%d!=%d",n,y);
}
int jc(int n)
{
 int r;
 if(n ==  0||n== 1)
 r=1;
 else r=n*jc(n-1);
 return r;
 } 

理解递归思想可以从宏观和微观两个角度上来考虑：
（1）宏观：将定义的函数jc理解为一个黑匣子，只需知道它可以将算出n！即可。
（2）微观：体会黑匣子的工作过程。计算n!时需算n*（n-1)！，算(n-1)!时需算(n-1)(n-2)!并依次类推到最后n=2时，2=21！，而1！可以算出它为1，于是得出2！=2，返回上一层求出3！，再依次返回到n!并求出该值。
这就是递归的思想
②返回到汉罗塔问题
(1)先手动体会汉罗塔问题：


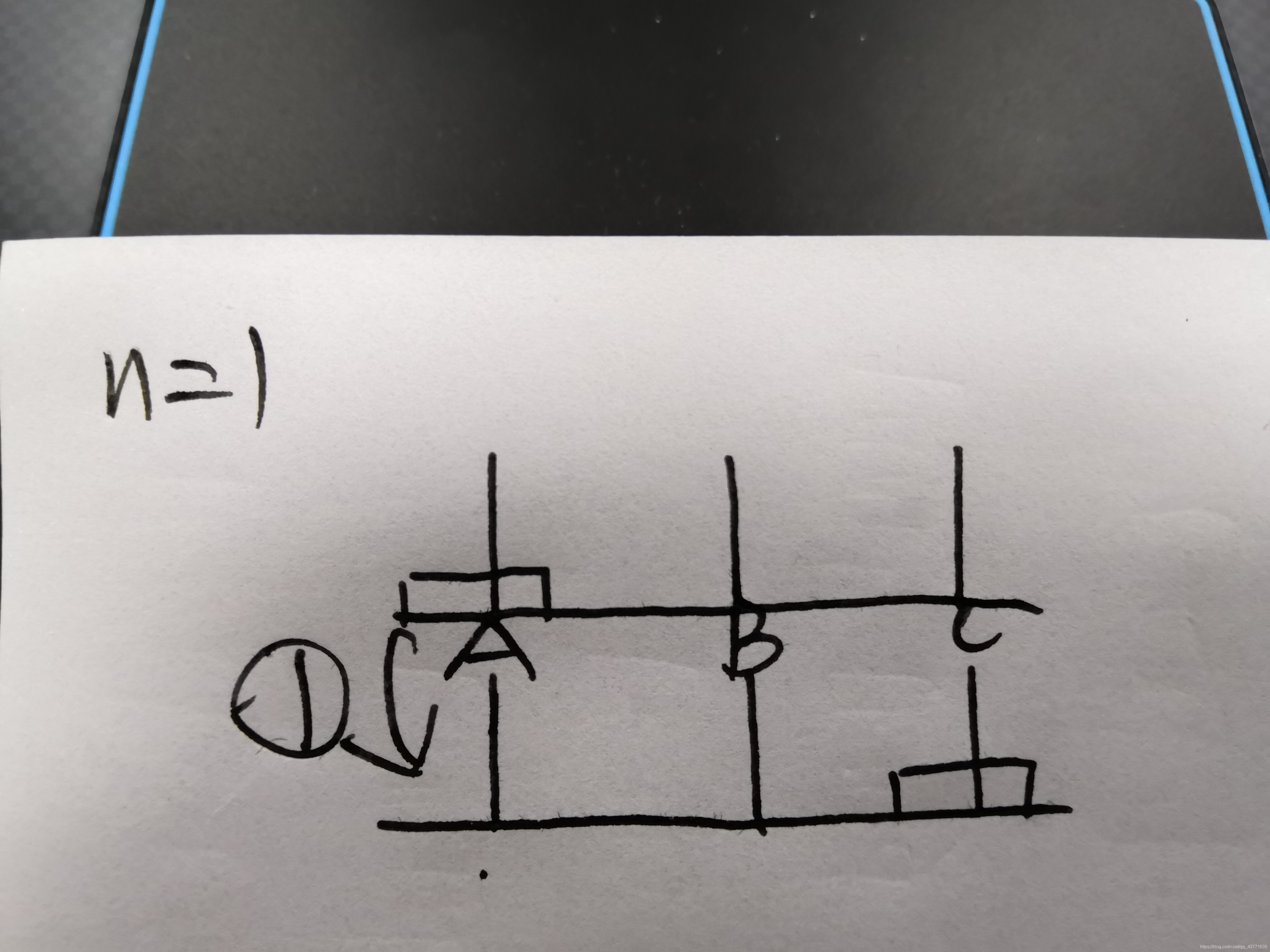
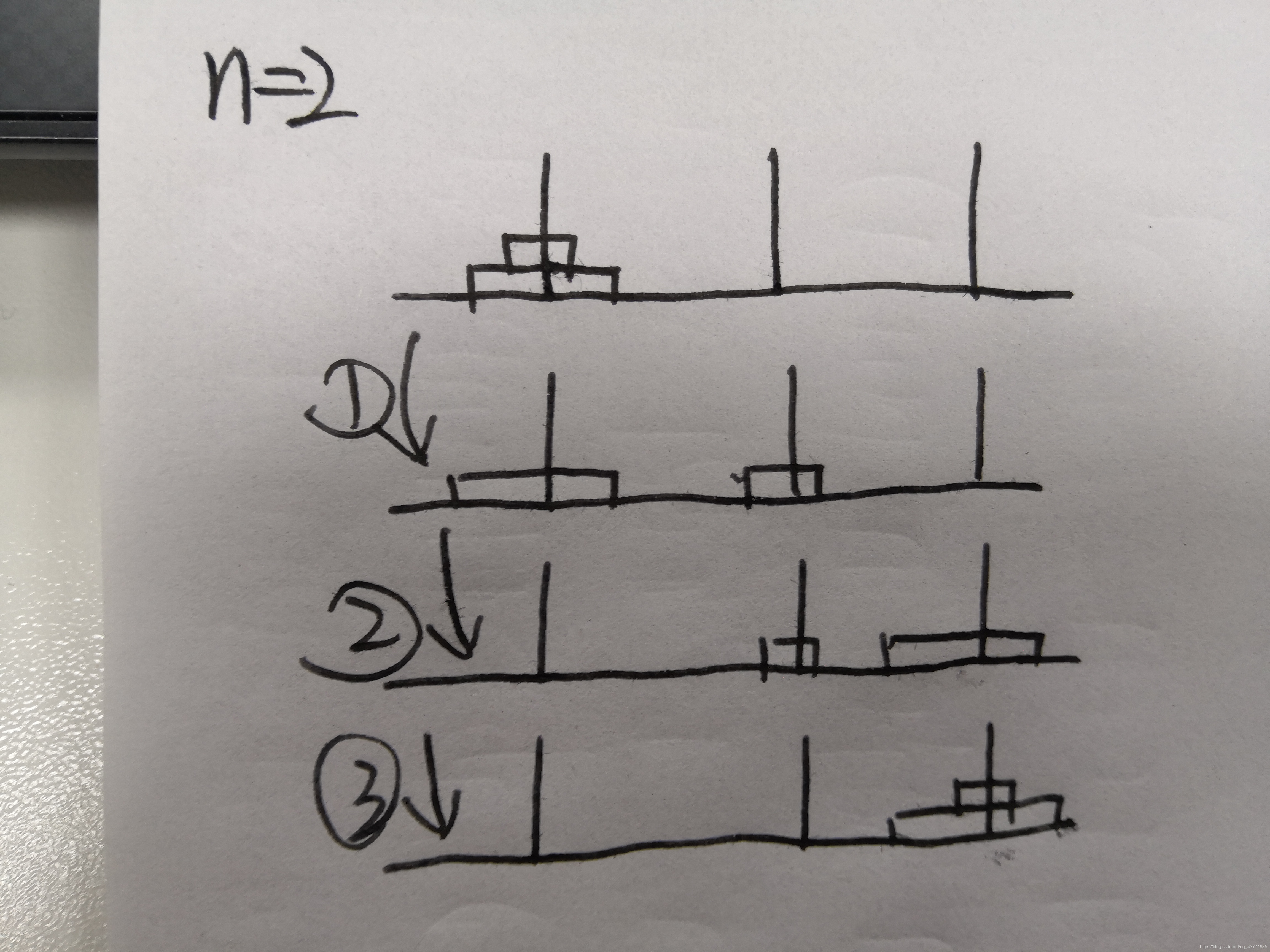
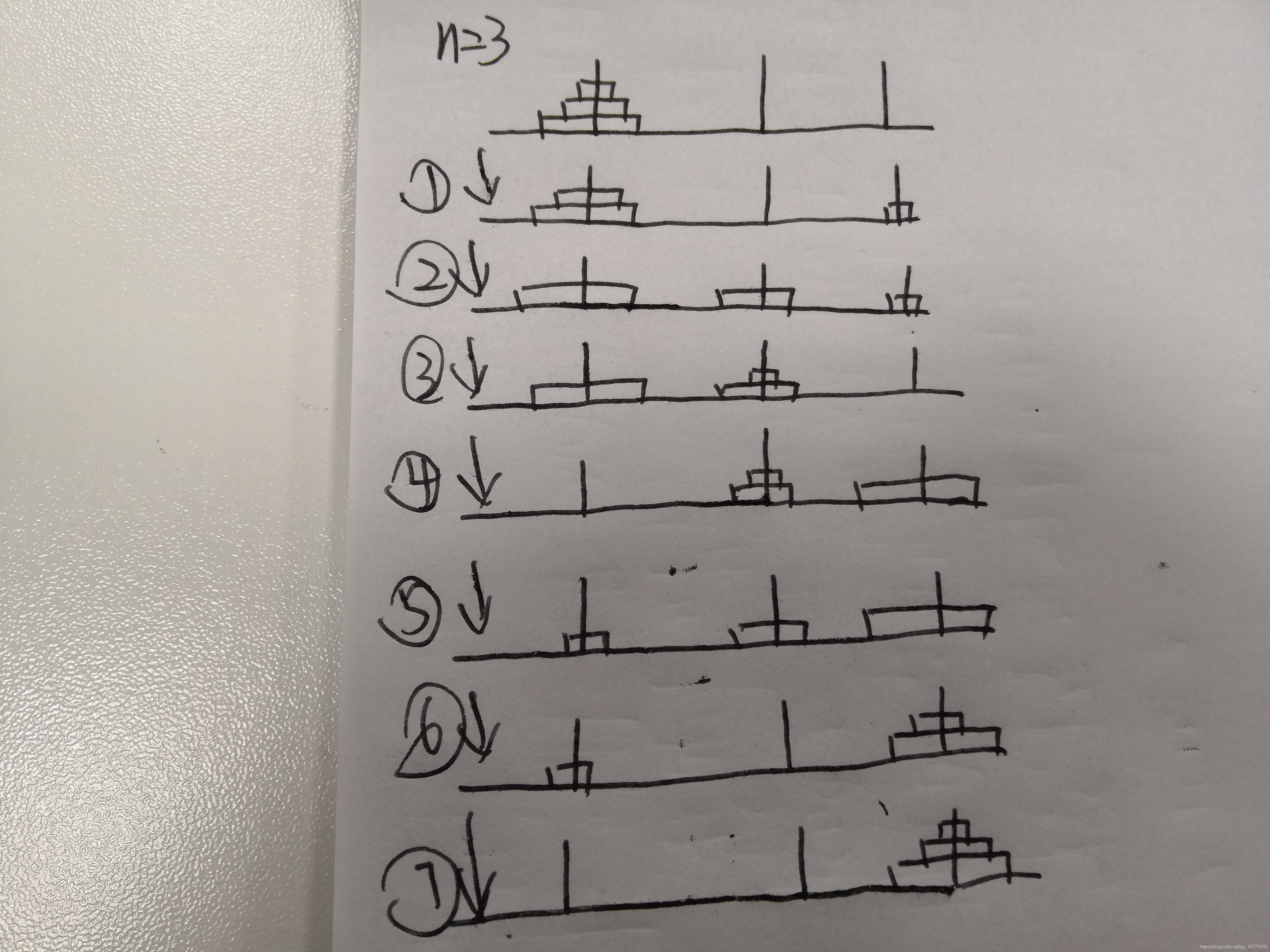
分析：n=1时，直接将A柱上一块，移到C柱上；n=2时，先将第一块移从A柱上移到B柱上，再将A柱上第二块移到C柱上，最后将B柱上的小块移到C柱上；n=3时，可以将过程理解为对n=2情况的模拟：先将上面两块从A柱移到B柱上（图中①②③步实现），再将最大的一块从A柱移到C柱上（第④步实现），最后将B柱上的两小块移到C柱上（⑤⑥⑦步实现）；由此可知n=1是一种单独的情况，n>=2既是同一种情况。
（2）构造函数：
（1）宏观上：该函数看做一个黑匣子，它的功能是将一个块从一根柱移动到另一根柱
黑匣子内部需要调用自身，但要正确排版。
n=1时：函数可以直接将块由A柱移动到C柱
n>=2时：函数的作用是：第一步将n-1块板移动到B柱，第二步将第n块板移动到C柱，第三步将之前的n-1块板移动到C柱上。
关键：第一步和第三步都是对该函数自身的调用。

（2）微观上：

汉罗塔问题的本身是一个经典的递归；先看n=2的情况：

由于n>1，像计算n的阶乘一样，n=2时得先计算1！；所以这里一样先计算参数为1的情况，还是同计算阶乘一样，函数在参数为1时，都可以直接计算，jc(1)=1,而这里实现的是将块由一根柱移动到另一根柱上（一定要注意起始柱和末柱究竟是哪两个）。就n=2的情况，因为n=2>1所以执行else部分，move(n-1,A,C,B)可以直接计算，由于起始柱是A末柱是B，于是函数计算的结果就是实现了将块由A移动到B；返回上一层，继续执行else部分，需要将第二块由A移动到C，这里需要直接用printf函数直接实现，如果用编辑的move（n-1…）,则在n>2时会出错，会使得这一步再一次调用本函数，出现多步，而这个位置永远只需要将最大的一块由A移动到C，所以直接printf实现；最后重复执行函数move(n-1,…)，将之前的最小块由B移动到C即可，所以参数应该变为move（n-1,B,A,C）,n-1=1还是可以就直接计算出将块由B移动到C。

n=2的情况就这样原原本本的实现了，于是就像计算阶乘一样，不断返回上一层，从而计算出不同的n的情况。
程序如下：

#include<stdio.h>
move(int n,char x,char y,char z)
{
 if(n==1)printf("%c-->%c\n",x,z);
      else {
       move(n-1,x,z,y);
       printf("%c-->%c\n",x,z);
       move(n-1,y,x,z);
   }
}
main()
{
 int n;
 scanf("%d",&n);
 move(n,'A','B','C');
}