力扣 11. 盛最多水的容器

最新推荐文章于 2025-03-16 23:44:31 发布

时光无错孤独难谈

最新推荐文章于 2025-03-16 23:44:31 发布

阅读量195

点赞数 1

分类专栏：力扣

本文链接：https://blog.youkuaiyun.com/qq_43745403/article/details/102979806

版权

力扣专栏收录该内容

2 篇文章

订阅专栏

本文介绍了一个使用双指针法解决的经典算法问题——寻找能容纳最多水的容器。通过对比两端高度，不断调整指针位置，最终找到最大盛水量。此方法巧妙地平衡了宽度与高度的关系。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：
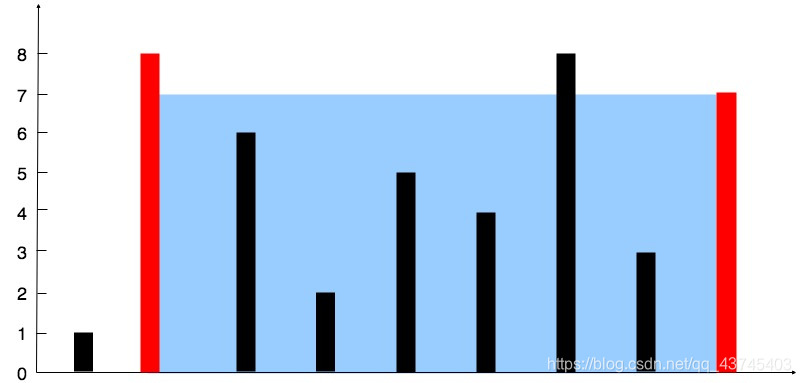
给定 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

在这里插入图片描述

Java：
class Solution {
    
    public int maxArea(int[] height) {
    	int l=0;
		int r=height.length-1;
		int v;
		int maxv=0;
		while(l!=r){
		if(height[l]<height[r]){
			v=(r-l)*height[l];
			l++;
		}
		else{
			v=(r-l)*height[r];
			r--;
		}
		maxv=maxv>v?maxv:v;
	}
	return maxv;     
    }
}

c
int maxArea(int* height, int heightSize){//双指针法 
	int l=0;//左 
	int r=heightSize-1;//右 
	int v;//中间变量 
	int maxv=0;//最大 
	while(l!=r){
		if(height[l]<height[r]){
			v=(r-l)*height[l];
			l++;//如果上一句前面便跳过第一个（下：最后一个）节点 
		}
//		if(height[l]>height[r]){
//			v=(r-l)*height[r];
//			r--;
//		}(如果有if，则时间复杂度增加o(n),成为2o(n)，else用来减少时间复杂度)
		else{
			v=(r-l)*height[r];
			r--;
		}
		maxv = maxv > v ? maxv : v ;
	}
	return maxv;
}

这个题用的双指针法。
想要得到盛最多水的容器，一方面要考虑他的宽度，一方面要考虑他的高度。
两方面都要考虑，所以可以先设定一个初值，max,来记录每次指针移动后的盛水的量，然后移动两端相比最小的那一边（已确保高度最大），直至遍历一遍（right==left）,将得到的max输出即可。