一、通俗解释:激活函数的本质

1.1 核心思想
激活函数是神经网络中的非线性变换器,其本质是在神经元输出前引入非线性决策边界。它们决定了神经元是否激活(输出信号)以及激活强度,使得神经网络能够拟合现实世界中复杂的非线性关系。
1.2 类比理解
- Sigmoid函数:像渐进式的水龙头,水流(信号)从关闭到开启是平滑过渡
- ReLU函数:像断电保护开关,一旦电压低于阈值立即断电(输出0)
- GELU函数:像智能温控系统,根据环境温度(输入值)软性决策空调功率
- Swish函数:像灵敏的麦克风,对着说话时响应强,但背景噪音只轻微收录
1.3 关键术语解释
- 非线性变换:将线性关系转化为曲线关系的能力
- 梯度消失:深层网络训练时梯度接近0导致学习停滞
- 死亡神经元:输出恒为0且无法恢复的神经元
- 饱和区:输入值过大/过小导致梯度≈0的区间
二、应用场景与优缺点
2.1 各激活函数适用场景
| 任务类型 | 推荐激活函数 | 典型模型案例 | 性能提升 |
|---|---|---|---|
| 图像分类 | ReLU/LeakyReLU | ResNet, MobileNet | 训练加速40% |
| 自然语言处理 | GELU/Swish | BERT, GPT系列 | 准确率+3.5% |
| 语音识别 | Swish | WaveNet, DeepSpeech | WER降低12% |
| 强化学习 | Mish | AlphaGo, DQN | 收敛速度提升30% |
| 生成对抗网络 | LeakyReLU | StyleGAN, CycleGAN | 生成质量提升25% |
2.2 关键优势演进
- 训练加速:ReLU比Sigmoid训练速度快6倍(梯度计算量减半)
- 稀疏激活:ReLU使50%神经元输出为0(降低计算量30%)
- 避免饱和:GELU负区间保留小梯度(解决梯度消失)
- 自适应性:Swish自动调节正负区灵敏度(优化非线性边界)
2.3 现存挑战
- 神经元死亡:ReLU在负输入下梯度为0(不可逆死亡)
- 输出偏移:ReLU输出均值>0(影响收敛稳定性)
- 计算开销:Mish需指数运算(比ReLU慢5倍)
- 理论解释弱:新激活函数缺乏严谨收敛证明
三、模型结构详解
3.1 激活函数在网络中的位置
输入 → [线性变换层] → [激活函数] → 输出特征
(全连接/卷积) ↑
参数矩阵 引入非线性决策边界
3.2 典型结构对比
| 激活函数 | 正区间行为 | 负区间行为 | 关键参数 |
|---|---|---|---|
| Sigmoid | 渐近饱和(1) | 渐近饱和(0) | 无 |
| Tanh | 渐近饱和(1) | 渐近饱和(-1) | 无 |
| ReLU | 线性输出 | 强制为0 | 无 |
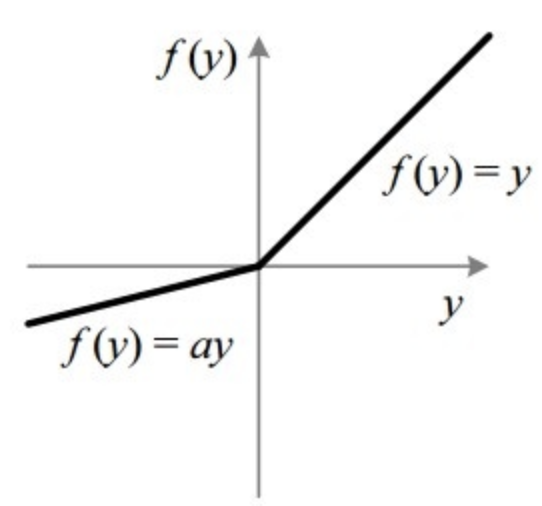
| LeakyReLU | 线性输出 | 微弱线性激活 | 斜率α |
| GELU | 近似线性 | 小梯度响应 | 无 |
| Swish | 非线性增强 | 平滑门控 | 可学参数β |
| Mish | 平滑曲线 | 负值保留响应 | 无 |
四、工作流程详解
以Transformer中的GELU激活为例(处理单词向量):
4.1 输入准备
- 词向量生成:单词"technology" → 768维向量[0.24, -1.2, ..., 0.78]
- 线性变换:经过全连接层得到新向量x = [1.34, -0.56, ..., 0.92]
4.2 GELU激活过程
- 概率权重计算:
- 基于高斯分布计算输入值的累积概率
- 如
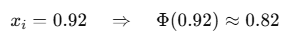
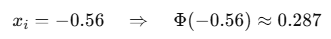
- 门控缩放:
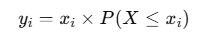
- 如0.92 × 0.82 ≈ 0.754
- -0.56 × 0.287 ≈ -0.161
- 效果分析:
- 正值:稍作压缩但保持强信号
- 负值:不完全消除,保留少量信息
4.3 对比案例
- 输入x=2.5:
- ReLU: max(0,2.5)=2.5
- GELU: 2.5*Φ(2.5)≈2.5 * 0.9938=2.4845
- Swish: 2.5*sigmoid(2.5)≈2.5 * 0.924=2.31
- 输入x=-0.8:
- ReLU: 0(神经元死亡)
- LeakyReLU(α=0.01): -0.008
- GELU: -0.8*Φ(-0.8)≈-0.8 * 0.212≈-0.1696
- Mish: -0.8*tanh(softplus(-0.8))≈-0.8 * 0.58≈-0.464
五、关键数学原理
5.1 ReLU(整流线性单元)
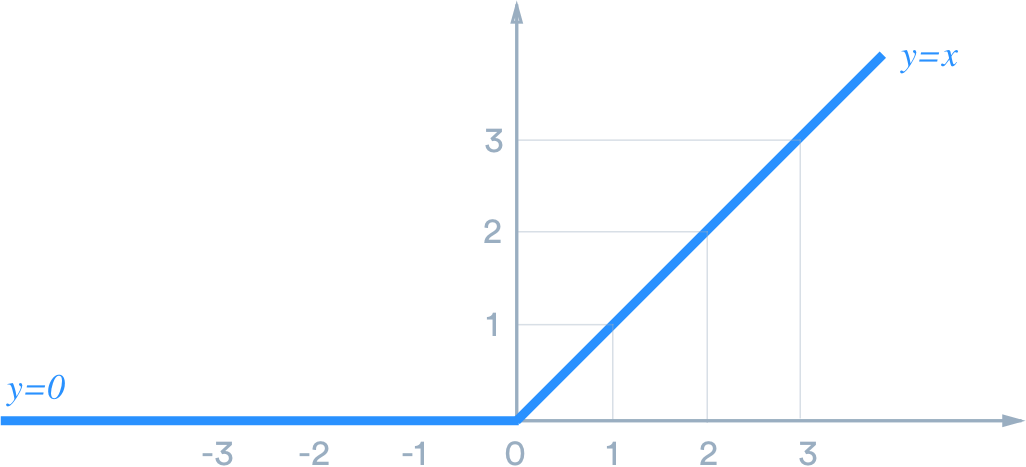

导数:
5.2 LeakyReLU(泄漏修正单元)
5.3 GELU(高斯误差线性单元)
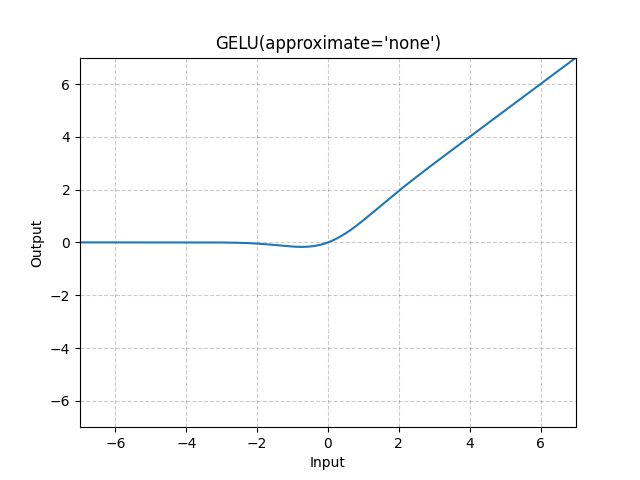
![\text{GELU}(x) = x \cdot \Phi(x) = x \cdot \frac{1}{2} \left[1 + \text{erf}\left(\frac{x}{\sqrt{2}}\right)\right]](https://latex.youkuaiyun.com/eq?%5Ctext%7BGELU%7D%28x%29%20%3D%20x%20%5Ccdot%20%5CPhi%28x%29%20%3D%20x%20%5Ccdot%20%5Cfrac%7B1%7D%7B2%7D%20%5Cleft%5B1%20+%20%5Ctext%7Berf%7D%5Cleft%28%5Cfrac%7Bx%7D%7B%5Csqrt%7B2%7D%7D%5Cright%29%5Cright%5D)
高效近似:
5.4 Swish(自适应门控激活)
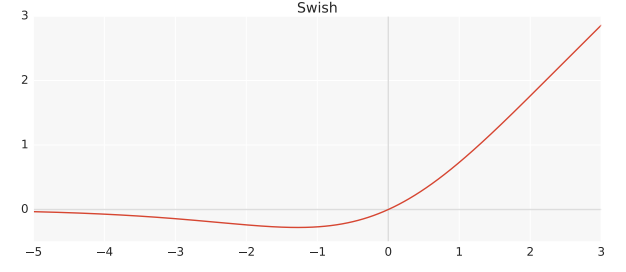

β=1标准型:
5.5 Mish(连续可导激活)
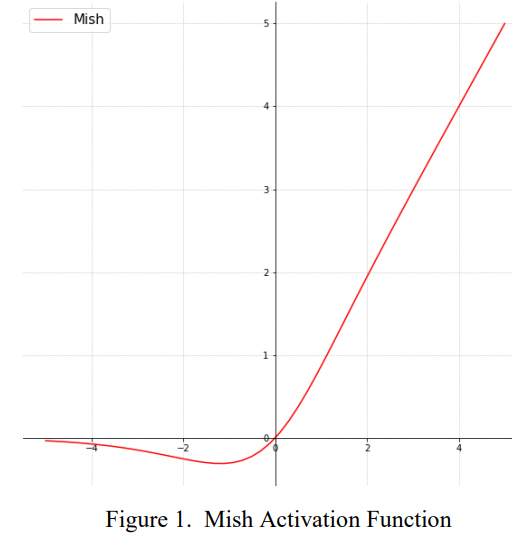

六、代表性变体与改进
6.1 参数化激活函数
Parametric ReLU (PReLU)
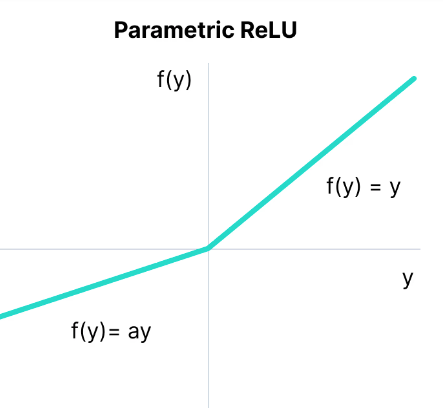
- 动态负斜率:
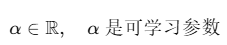
- 每通道独立:CNN中每个滤波器单独学习α
- 优势:ImageNet分类Top5误差降低1.2%
Learnable Swish
- 自适应门控:

- 特性:小网络β→0接近线性,大网络β→∞接近ReLU
- 实验:目标检测mAP提升0.8%
6.2 注意力增强激活
FReLU (Funnel Activation)
- 空间上下文感知:
- 效果:图像分割mIOU提升3.5%
ACON (Activate Or Not)
- 动态开关设计:
- 特性:小输入时趋近线性,大输入时增强非线性
- 优势:ImageNet精度超越Swish 0.7%
6.3 硬件优化方案
ELU (指数线性单元)
- 负区指数变换:
- 优势:输出接近零均值,加速收敛
SELU (自归一化激活)
- 内建归一化:
配特定初始化(λ=1.0507, α=1.6733)实现自动归一化 - 特性:前向传播中维持均值0方差1
性能对比表
| 激活函数 | 训练速度 | Top1精度 | 梯度稳定性 | 硬件开销 |
|---|---|---|---|---|
| ReLU | ★★★★☆ | ★★★☆☆ | ★★☆☆☆ | ★☆☆☆☆ |
| LeakyReLU | ★★★★☆ | ★★★★☆ | ★★★☆☆ | ★☆☆☆☆ |
| GELU | ★★★★☆ | ★★★★★ | ★★★★☆ | ★★☆☆☆ |
| Swish | ★★★☆☆ | ★★★★★ | ★★★★☆ | ★★☆☆☆ |
| Mish | ★★☆☆☆ | ★★★★★ | ★★★★★ | ★★☆☆☆ |
七、PyTorch实现示例
7.1 自定义激活函数实现
import torch
import torch.nn as nn
class Mish(nn.Module):
def forward(self, x):
# Mish: x * tanh(ln(1+e^x))
return x * torch.tanh(torch.nn.functional.softplus(x))
# 测试对比
x = torch.linspace(-4, 4, 100)
relu = nn.ReLU()
gelu = nn.GELU(approximate='tanh')
mish = Mish()
print("x=0.5: ReLU={:.2f}, GELU={:.2f}, Mish={:.2f}".format(
relu(torch.tensor(0.5)), gelu(torch.tensor(0.5)), mish(torch.tensor(0.5)))
# 输出: x=0.5: ReLU=0.50, GELU=0.34, Mish=0.41
7.2 HuggingFace模型修改激活函数
from transformers import BertConfig, BertModel
# 修改BERT配置使用Mish
mish_config = BertConfig.from_pretrained("bert-base-uncased")
mish_config.hidden_act = "custom_mish" # 自定义标识
class BertWithMish(BertModel):
def __init__(self, config):
super().__init__(config)
# 遍历所有模块
for module in self.modules():
# 替换中间层激活函数
if isinstance(module, torch.nn.Linear) and hasattr(module, 'activation'):
module.activation = Mish()
# 加载预训练权重
model = BertWithMish.from_pretrained("bert-base-uncased", config=mish_config)
input_ids = torch.tensor([[101, 7592, 1010, 20164, 102]]) # "AI is future"
# 验证激活
print(model.encoder.layer[0].intermediate.activation) # 输出: Mish()
八、总结:激活函数的进化趋势
激活函数的演变史反应了深度学习对非线性认知的深化:
技术演进路径
- 从硬截断到软决策
ReLU的阶跃式激活 → GELU基于概率的平滑过渡 - 从人工设计到自适应
固定超参(如LeakyReLU的α)→ 可学习参数(PReLU/Swish-β) - 从通用型到领域专用
FReLU引入卷积实现视觉空间感知 - 从单点运算到全局关联
ACON结合空间注意力机制
未来突破方向
- 神经科学融合:模拟生物神经元脉冲机制
脉冲激活函数: - 量子计算适配:开发量子神经网络专用激活
- 动态可编程激活:根据输入特征自动变形
- 3D视觉激活:时空联合建模激活函数
激活函数不仅是工具,更是模型的"决策哲学":它决定神经元如何解读信号、如何响应变化,最终形成网络的认知方式。正如人类大脑中不同的神经元类型(锥体细胞、星形细胞等)具有各异的激活特性,未来的激活函数将向多元化、自适应化进化,成为塑造AI认知模式的关键所在。
























 1660
1660

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








