Codeforces - 578C Round Corridor（数学 + 模拟）

Huffman_Tree_

于 2019-08-12 17:18:46 发布

阅读量231

点赞数

CC 4.0 BY-SA版权

分类专栏： CodeForces

转载请注明出处//https://blog.youkuaiyun.com/qq_43658924

本文链接：https://blog.youkuaiyun.com/qq_43658924/article/details/99312448

CodeForces 专栏收录该内容

53 篇文章

订阅专栏

本文解析一道算法竞赛题目，通过计算内外两部分可互相走动的块数，利用最大公因数（gcd）函数简化问题，实现快速判断两组坐标是否在同一块内的算法。核心在于对输入坐标进行预处理，通过除以内外部分的最大公因数得出标准化的块号，从而判断坐标是否位于同一块。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

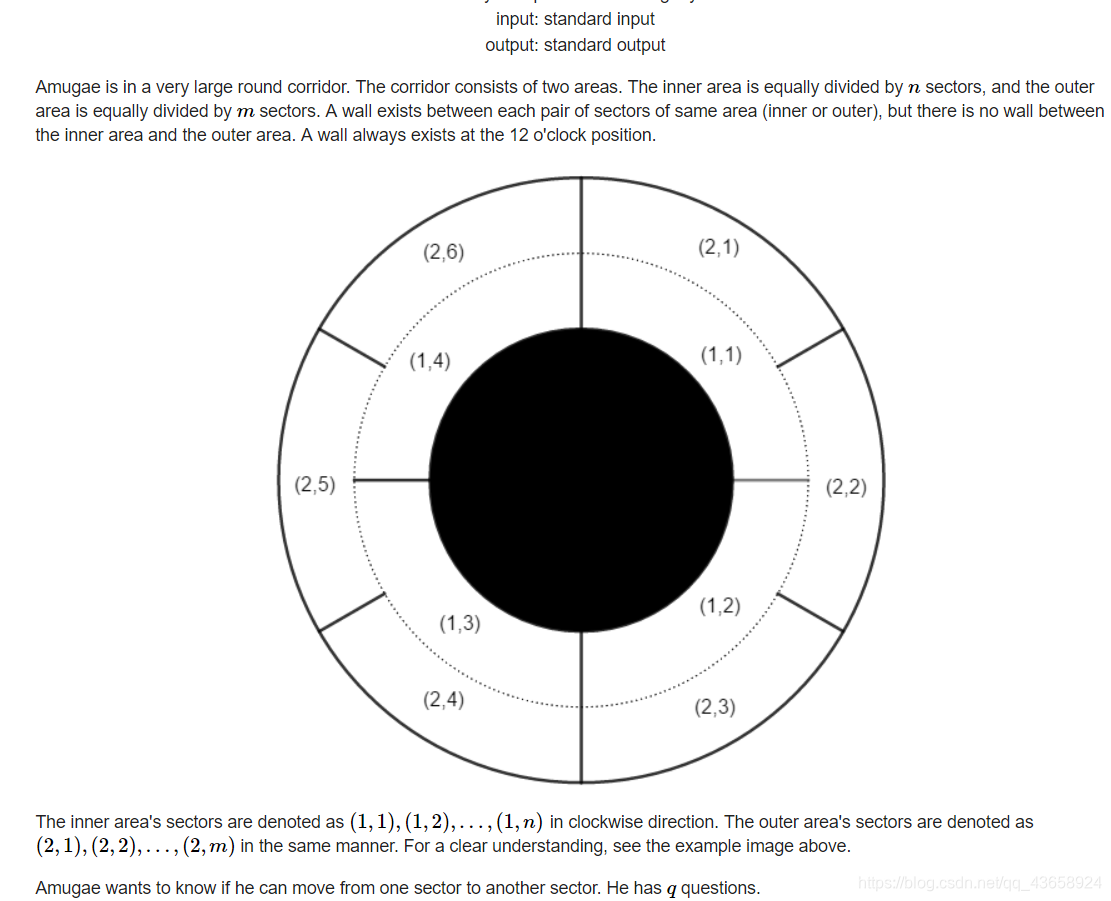
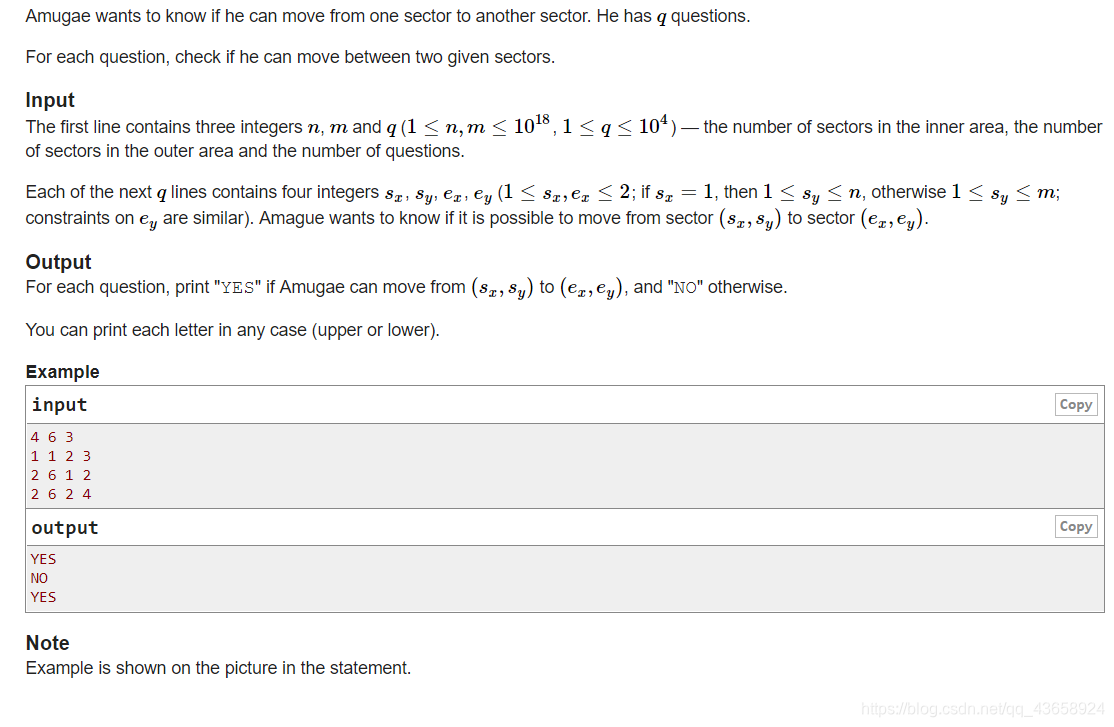
在这里插入图片描述

题目理解：
比较需要注意的是题目中内外对应分块的处理，一开始可以从所有情况列举开始考虑
最后合并能推出
(a1-1)/n/gcd(n,m)==(a2-1)/n/gcd(n,m)
然后求最大公因数可以

直接调用gcd或者__gcd 头是而不是

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int q;
ll n,m,k[3],a1,a2,b1,b2;
int main(){
	cin>>n>>m>>q;
	k[1]=n/gcd(n,m);k[2]=m/gcd(n,m);
	//gcd使用原因
	//分别是内外两部分中可以互相走动的所涉及的块数
	while(q--){
		cin>>b1>>a1>>b2>>a2;
		if((a1-1)/k[b1]==(a2-1)/k[b2])cout<<"YES\n";
		//核心。
		//输入y坐标的时候就默认考虑了均分块数的情况，直接调用y即可
		//同时要注意a1-1就不用考虑边界了
		else cout<<"NO\n";
	}
}