HDU 4507 吉哥系列故事——恨7不成妻（数位DP）

本文链接：https://blog.youkuaiyun.com/qq_43653111/article/details/104339904

本文探讨了一种复杂的数位动态规划(DP)问题，旨在统计满足特定条件的数的平方和。通过详细的代码解析，讲解了如何构建并维护计数、总和及平方和的结构体，同时考虑了进制转换、模运算等细节，为解决类似问题提供了清晰的思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

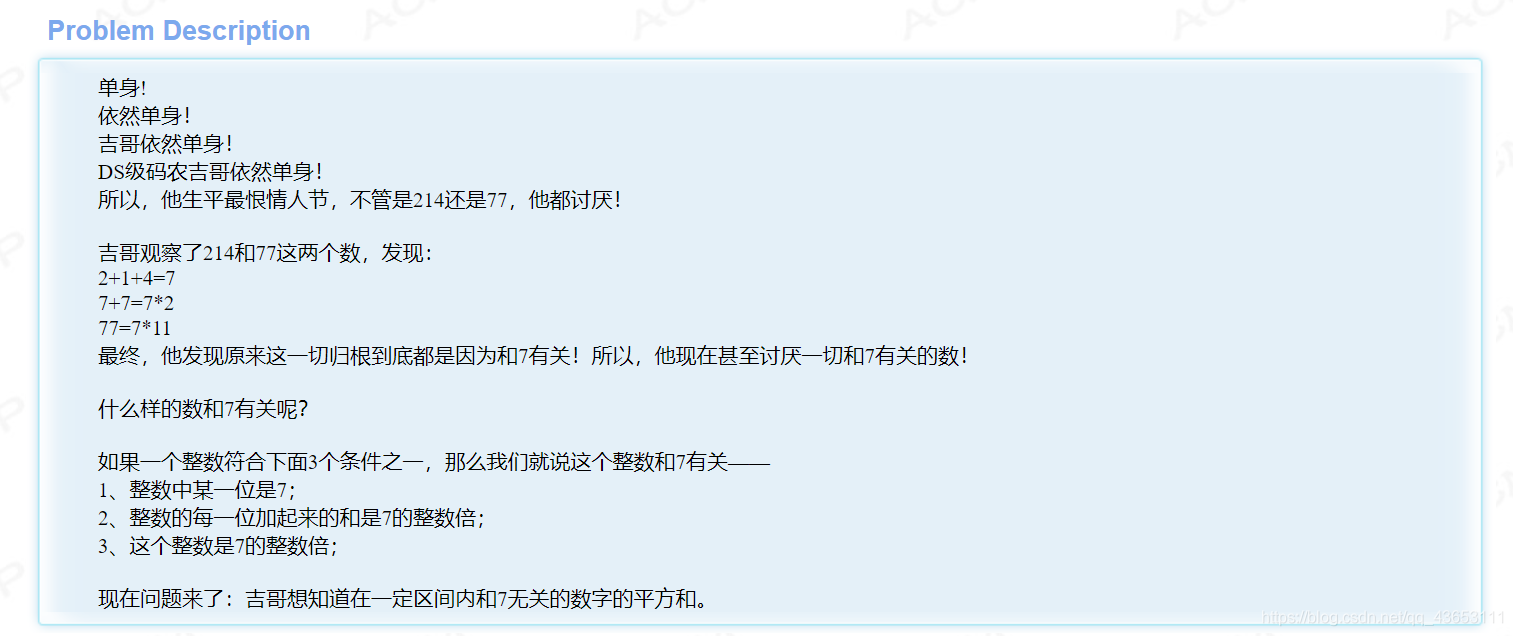
在这里插入图片描述
与7不沾边的数需要满足三个条件。
①不出现7
②各位数和不是7的倍数
③这个数不是7的倍数

这三个条件都是基础的数位DP。

但是这题要统计的不是符合条件个数，而是平方和。

也就是说在DP时候，要重建每个数，算出平方，然后求和。
需要维护三个值（推荐使用结构体）, 假定dfs推出返回的结构体是next，当前结果的结构体是ans
①符合条件数的个数 cnt
②符合条件数的和 sum
③符合添加数的平方和 pow

其中①是基础数位DP。②next.sum+(10^len * i) * next.cnt，其中(10^len*i)*ans.cnt代表以len为首位的这部分数字和。

③首先重建一下这个数，(10^len * i+x),其中x是这个数的后面部分，则平方和就是(10^len * i)^2+x ^2 + 2*10^len *i *x，其中x^2=next.sqsum

整体还要乘以next.cnt，毕竟不止一个。

这样sqsum+=next.sqsum

sqsum+=(2 * 10^len * i * x) * next.cnt=(2 * 10^len* i)*next.sum

sqsum+=(10^len * i)^2*next.cnt

注意的点：
1.(ans+mod)%mod，ans可能是负数
2.dp初始化
3.POW[i]=10^(i-1);

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+4;
const int mod=1e9+7;
ll l,r,a[20],POW[20];
struct node
{
    ll cnt,sum,pow;
    node()
    {
        cnt=-1,sum=0,pow=0;
    }
    node(ll a,ll b,ll c):cnt(a),sum(b),pow(c){}
} dp[20][10][10];
node dfs(ll now,ll sum1,ll sum2,ll limit)
{
    if(!now)
    {
        node tmp;
        tmp.cnt=(sum1&&sum2);
        tmp.sum=tmp.pow=0;
        return tmp;
    }
    if(!limit&&~dp[now][sum1][sum2].cnt)
        return dp[now][sum1][sum2];
    ll up=limit?a[now]:9;
    node ans(0,0,0);
    for(ll i=0; i<=up; i++)
    {
        if(i==7)
            continue;
        node next=dfs(now-1,(sum1+i)%7,(sum2*10+i)%7,limit&&i==up);
        (ans.cnt+=next.cnt)%=mod;
        (ans.sum+=(next.sum+POW[now]*i%mod*next.cnt%mod)%mod)%=mod;
        (ans.pow+=(next.pow+(2*POW[now]%mod*i%mod*next.sum%mod))%mod)%=mod;
        (ans.pow+=i*i*POW[now]%mod*POW[now]%mod*next.cnt%mod)%=mod;
    }
    if(!limit)
        dp[now][sum1][sum2]=ans;
    return ans;
}
ll solve(ll num)
{
    a[0]=0;
    while(num)
    {
        a[++a[0]]=num%10;
        num/=10;
    }
    return dfs(a[0],0,0,1).pow;
}
void init()
{
    POW[1]=1;
    for(int i=2; i<=20; i++)
        POW[i]=(10*POW[i-1])%mod;
}
int main()
{
    init();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%lld",&l,&r);
        printf("%lld\n",(solve(r)-solve(l-1)+mod)%mod);
    }






}