EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation Maximization Algorithm)。EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题。
例如当两种高斯分布的人混在一块了,我们又不知道哪些人属于第一个高斯分布,哪些属于第二个,所以就没法估计这两个分布的参数。反过来,只有当我们对这两个分布的参数作出了准确的估计的时候,才能知道到底哪些人属于第一个分布,那些人属于第二个分布。所以这里就是说EM估计就是因为多了一个隐含变量(抽取得到的每个样本都不知道是从哪个分布抽取的)使得本来简单的可以求解的问题变复杂了。
EM算法的推导
随机变量
X
X
X是有
K
K
K个高斯分布混合而成,取各个高斯分布的概率为
π
1
,
π
2
,
⋅
⋅
⋅
,
π
K
。
若
观
测
到
随
机
变
量
\pi_1,\pi_2,···,\pi_K。若观测到随机变量
π1,π2,⋅⋅⋅,πK。若观测到随机变量X$的一系列样本:
x
1
,
x
2
,
.
.
.
,
x
m
x_1,x_2,...,x_m
x1,x2,...,xm,包含m个独立样本,希望从中找到该组数据的模型
p
(
x
,
z
)
p(x,z)
p(x,z)的参数。
对于这样多个高斯分布混合而成的模型,称作高斯混合模型(GMM)。

取对数似然函数
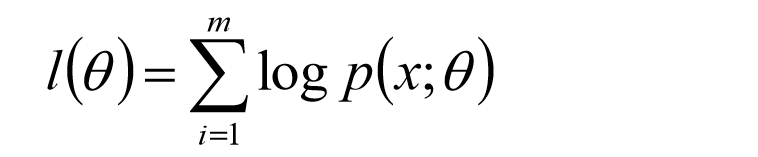
由于样本来自不同的高斯分布,我们并不知道每个样本来自哪个分布,因此这个似然函数无法求解。一个方法是考虑隐变量,用z标记样本来自哪个总体,则z就是隐变量,需要最大化的似然函数就变为:

似然函数求解
z是隐随机变量,不方便直接找到参数估计。策略:计算
l
(
θ
)
l(\theta)
l(θ)下界函数,求该下界的最大值;重复该过程,直到收敛到局部最大值。

Jensen不等式

当x为常数时等号成立。
令
Q
i
Q_i
Qi是z的某一个分布,
Q
i
>
=
0
Q_i>=0
Qi>=0,有:
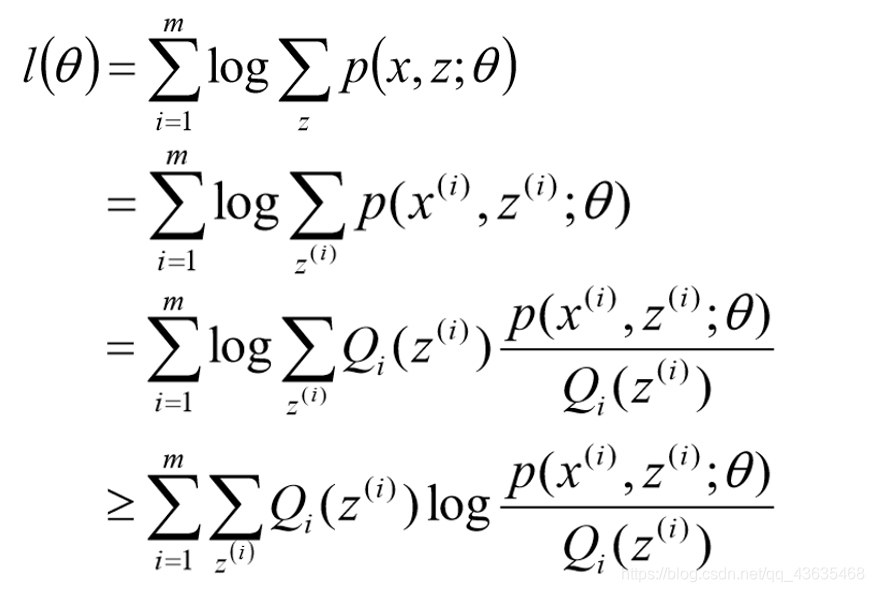
寻找尽量紧的下界
为了使等号成立:


得到
Q
(
z
)
Q(z)
Q(z),大功告成,
Q
(
z
)
Q(z)
Q(z)就是
p
(
z
i
∣
x
i
)
p(z_i|x_i)
p(zi∣xi),或者写成
p
(
z
i
)
p(z_i)
p(zi),代表第
i
i
i个数据是来自
z
i
z_i
zi的概率。
EM算法整体框架
首先,初始化参数θ
(1)E-Step:根据参数
θ
θ
θ计算每个样本属于
z
i
z_i
zi的概率,这个概率就是
Q
Q
Q;
(2)M-Step:根据计算得到的
Q
Q
Q,求出含有
θ
θ
θ的似然函数的下界并最大化它,得到新的参数
θ
θ
θ;
重复(1)和(2)直到收敛。







 本文深入探讨了EM算法(期望最大化算法)的基本原理及其在处理数据缺失情况下的应用。EM算法通过迭代优化策略,解决高斯混合模型(GMM)中参数估计问题。文章详细介绍了EM算法的E步和M步,并通过实例解释了算法如何处理隐含变量带来的复杂性。
本文深入探讨了EM算法(期望最大化算法)的基本原理及其在处理数据缺失情况下的应用。EM算法通过迭代优化策略,解决高斯混合模型(GMM)中参数估计问题。文章详细介绍了EM算法的E步和M步,并通过实例解释了算法如何处理隐含变量带来的复杂性。
















 1503
1503

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








