组合数&&杨辉三角

最新推荐文章于 2024-07-30 14:12:26 发布

原创

最新推荐文章于 2024-07-30 14:12:26 发布 · 301 阅读

0 ·

CC 4.0 BY-SA版权

本文探讨了组合数的概念，即从n个不同元素中取出m个元素的组合数。当数据较大或精度要求高时，直接使用公式计算可能会消耗大量时间和空间。通过介绍杨辉三角，展示了它在解决组合数问题上的应用。通过二维数组和递归两种方式实现杨辉三角，以优化计算效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

你做过组合数吗？
所谓的组合数：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n)个元素的所有组合的个数（来自百度百科，学数学的时候也没有记住准确的概念…）
我们都知道，求组合数的公式：
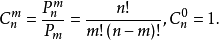
在这里插入图片描述
当然，从公式中我们可以发现，只要按照公式中给出的阶乘相除来得到，但是如果数据很大，或者说要求的精度高的计算中，我们需要耗费的时间和空间往往会超出我们的想象。
但是，很神奇的是，杨辉三角这个古代数学家杨辉的智慧结晶可以帮助我们来处理组合数的问题，有惊人的相似性。之前上数学课学习这个杨辉三角时，老师说不考，基本上没仔细看过…好吧是我的错。
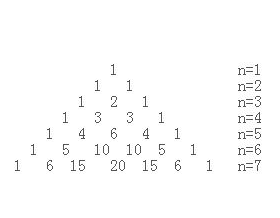
我们可以发现，与组合数完全一致
巧了，这个真的和组合数相一致。向古代伟大的数学家致敬。
不难想到，我们可以用二维数组来实现。
上代码：

#include<stdio.h>
int main()
{
   
   
	int n,a[101][101]={
   
   0},i,j;
	scanf("%d",&n);
	for(i=1;i<=n;i++

最低0.47元/天解锁文章

200万优质内容无限畅学