题目描述
当前有N件物品和一个容积为V的背包。已知第i件物品的体积是Ci,价值是Wi。
由于每种物品有且仅有一件,因此只能选择放或不放,我们称之为01背包问题。
现在你需要选出若干件物品,在它们的重量之和不超过V的条件下,使得价值总和尽可能大。
对于01背包,先确定这个问题的状态。共有N个物品,背包总承重为V,那么可以根据物品和容量来确定一个状态。前i个物品,放在背包里,总重量不超过j的前提下,所获得的最大价值为dp[i][j]。
是否将第i个物品装入背包中,就是决策。为了使价值最大化,如果第i个物品放入背包后,总重量不超过限制且总价值比之前要大,那么就将第i个物品放入背包。根据这个逻辑写出转移方程:
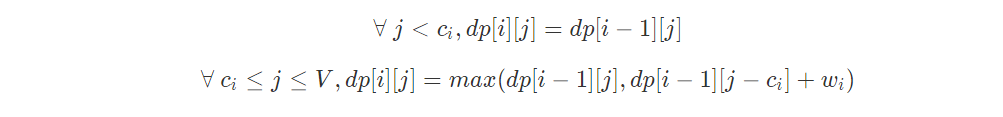
核心代码:
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
if(j >= c[i])
{
dp[i][j] = max(dp[i - 1][j - c[i]] + w[i], dp[i - 1][j]);
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
}
优化空间复杂度:
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
if(j >= c[i])
{
dp[i][j] = max(dp[i - 1][j - c[i]] + w[i], dp[i - 1][j]);
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
}








 本文深入探讨了01背包问题的解决策略,通过动态规划方法,详细解释了如何在有限背包容量下,从N件不同体积与价值的物品中选择,以达到价值最大化的最优解。文章提供了核心代码及空间复杂度优化方案。
本文深入探讨了01背包问题的解决策略,通过动态规划方法,详细解释了如何在有限背包容量下,从N件不同体积与价值的物品中选择,以达到价值最大化的最优解。文章提供了核心代码及空间复杂度优化方案。
















 222
222

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








