一、随机选取枢轴
适用于待排序列为部分有序时,固定选枢轴导致效率低下。
/*随机选择枢轴的位置,区间在low和high之间*/
int SelectPivotRandom(int arr[],int low,int high)
{
//产生枢轴的位置
srand((unsigned)time(NULL));
int pivotPos = rand()%(high - low) + low;
//把枢轴位置的元素和low位置元素互换,此时可以和普通的快排一样调用划分函数
swap(arr[pivotPos],arr[low]);
return arr[low];
}
总结:这是一种相对安全的策略。由于枢轴的位置是随机的,那么产生的分割也不会总是会出现劣质的分割。在整个数组数字全相等时,仍然是最坏情况,时间复杂度是O(n ^ 2)。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。但是无法具有大量重复数据的序列。
二、三数取中
/*函数作用:取待排序序列中low、mid、high三个位置上数据,选取他们中间的那个数据作为枢轴*/
int SelectPivotMedianOfThree(int arr[],int low,int high)
{
int mid = low + ((high - low) >> 1);//计算数组中间的元素的下标
//使用三数取中法选择枢轴
if (arr[mid] > arr[high])//目标: arr[mid] <= arr[high]
{
swap(arr[mid],arr[high]);
}
if (arr[low] > arr[high])//目标: arr[low] <= arr[high]
{
swap(arr[low],arr[high]);
}
if (arr[mid] > arr[low]) //目标: arr[low] >= arr[mid]
{
swap(arr[mid],arr[low]);
}
//此时,arr[mid] <= arr[low] <= arr[high]
return arr[low];
//low的位置上保存这三个位置中间的值
//分割时可以直接使用low位置的元素作为枢轴,而不用改变分割函数了
}
总结:和上一个优化方案半斤八两,但是这两个方案都有一个共同的问题,无法处理重复数据。
优化1、当待排序序列的长度分割到一定大小后,使用插入排序。
原因:对于很小和部分有序的数组,快排不如插排好。当待排序序列的长度分割到一定大小后,继续分割的效率比插入排序要差,此时可以使用插排而不是快排
if (high - low + 1 < 10)
{
InsertSort(arr,low,high);
return;
}//else时,正常执行快排
优化2、在一次分割结束后,可以把与Key相等的元素聚在一起,继续下次分割时,不用再对与key相等元素分割(解决序列中含有大量重复数据)
具体过程:
第一步,在划分过程中,把与key相等元素放入数组的两端
第二步,划分结束后,把与key相等的元素移到枢轴周围
举例:
待排序序列
1 4 6 7 6 6 7 6 8 6
三数取中选取枢轴:下标为4的数6
转换后,待分割序列:
6 4 6 7 1 6 7 6 8 6
枢轴key:6
第一步,在划分过程中,把与key相等元素放入数组的两端
结果为:
6 4 1 6(枢轴) 7 8 7 6 6 6
此时,与6相等的元素全放入在两端了
第二步,划分结束后,把与key相等的元素移到枢轴周围
结果为:
1 4 66(枢轴) 6 6 6 7 8 7
void QSort(int arr[],int low,int high)
{
int first = low;
int last = high;
int left = low;
int right = high;
int leftLen = 0;
int rightLen = 0;
if (high - low + 1 < 10)
{
InsertSort(arr,low,high);
return;
}
//一次分割
int key = SelectPivotMedianOfThree(arr,low,high);//使用三数取中法选择枢轴
while(low < high)
{
while(high > low && arr[high] >= key)
{
if (arr[high] == key)//处理相等元素
{
swap(arr[right],arr[high]);
right--;
rightLen++;
}
high--;
}
arr[low] = arr[high];
while(high > low && arr[low] <= key)
{
if (arr[low] == key)
{
swap(arr[left],arr[low]);
left++;
leftLen++;
}
low++;
}
arr[high] = arr[low];
}
arr[low] = key;
//一次快排结束
//把与枢轴key相同的元素移到枢轴最终位置周围
int i = low - 1;
int j = first;
while(j < left && arr[i] != key)
{
swap(arr[i],arr[j]);
i--;
j++;
}
i = low + 1;
j = last;
while(j > right && arr[i] != key)
{
swap(arr[i],arr[j]);
i++;
j--;
}
QSort(arr,first,low - 1 - leftLen);
QSort(arr,low + 1 + rightLen,last);
}
结论:
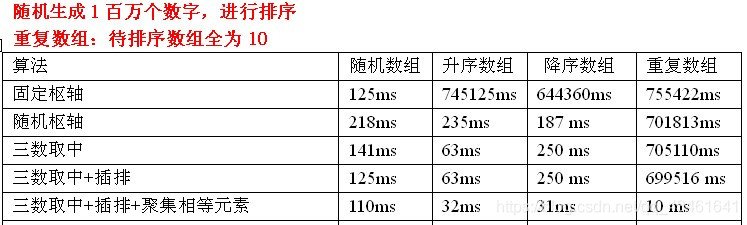







 本文探讨了快速排序算法的两种优化策略:随机选取枢轴和三数取中法,旨在提高排序效率并解决部分有序和重复数据问题。同时,介绍了如何在小规模数据使用插入排序,以及如何处理大量重复数据,通过将相等元素聚集来提升分割效率。
本文探讨了快速排序算法的两种优化策略:随机选取枢轴和三数取中法,旨在提高排序效率并解决部分有序和重复数据问题。同时,介绍了如何在小规模数据使用插入排序,以及如何处理大量重复数据,通过将相等元素聚集来提升分割效率。
















 2775
2775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








