高级数据结构——伸展树（Splay Tree）

什么是伸展树？

伸展树（Splay Tree）是一种二叉搜索树，它能在O(log n)内完成插入、查找和删除操作。它由Daniel Sleator和Robert Tarjan创造。它的优势在于不需要记录用于平衡树的冗余信息。在伸展树上的一般操作都基于伸展操作。

为什么需要伸展树？

各种二叉搜索树存在不足。比如：对于一个有n个节点的平衡二叉搜索树，虽然最坏情况下每次查找的时间复杂度不会超过O(logn)，但是如果访问模式不均匀，平衡树的效率就会受到影响。此外，它们还需要额外的空间来存储平衡信息（结点的高度）。

伸展树的简单概述

伸展树对具有“数据局部性”的数据单元来说，最为适合。
假设想要对一个二叉搜索树执行一系列的查找操作。为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法，在每次查找之后对树进行重构，把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。splay tree是一种自调整形式的二叉搜索树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

重构方法

1. 单旋：在查找完位于节点x中的条目i之后，旋转链接x和其父节点的边。（除非x就是树根）
2. 搬移至树根：在查找完位于节点x中的条目i之后，旋转链接x和其父节点的边，然后重复这个操作直至x成为树根。

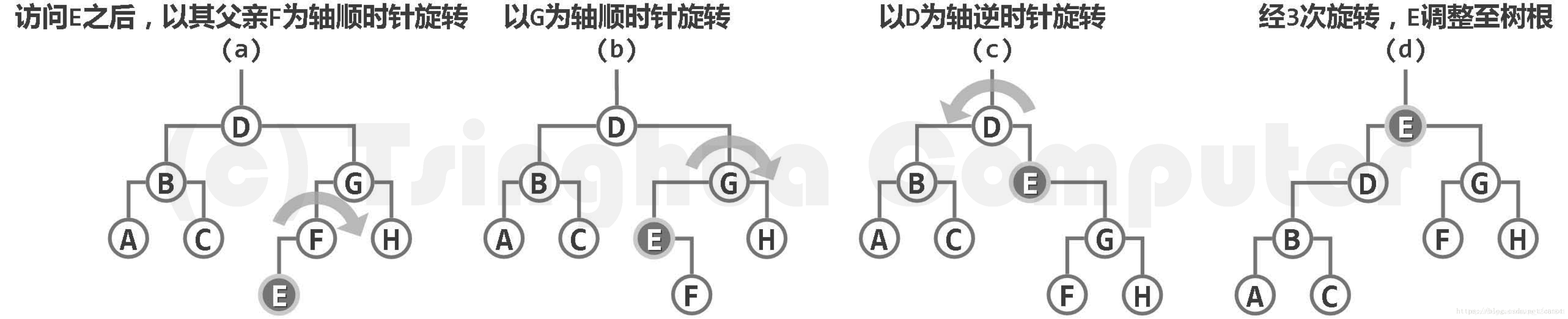
伸展树的缺陷

若从空树开始依次插入关键码{ 1, 2, 3, 4, 5 }，且其间采用如上调整策略，
则可得到如下图所示的二叉搜索树。

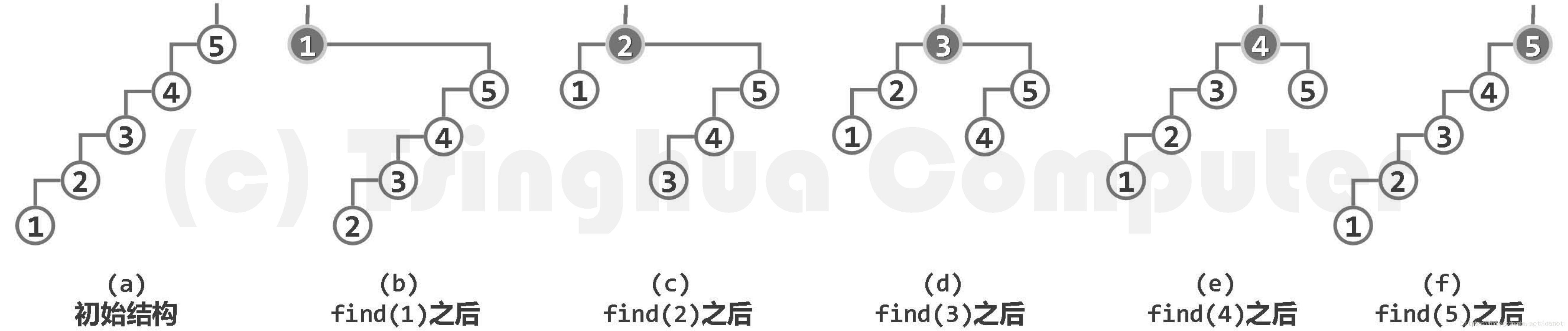
如此分摊下来，每次访问平均需要n时间。
且上图a与f中二叉搜索树的结构完全相同。也就是说，经过以上连续的5次访问之后，全树的结构将会复原!
完全可以推广至规模任意的二叉搜索树。于是对于规模为任意n的伸展树， 只要按关键码单调的次序，周期性地反复进行查找，则无论总的访问次数m >> n有多大，就分摊意义而言，每次访问都将需要n时间!

伸展树的改进

双层伸展
可见，最深节点(1)被访问之后再经过双层调整，不仅同样可将该节点伸展至树根，而且同时可使树的高度接近于减半。就树的形态而言，双层伸展策略可“智能”地“折叠”被访问的 子树分支，从而有效地避免对长分支的连续访问。这就意味着，即便节点v的深度为n，双层 伸展策略既可将v推至树根，亦可令对应分支的长度以几何级数(大致折半)的速度收缩。