参考文献:
【1】详解逻辑回归(LR)计算过程_这里记录着我一点一滴的进步-优快云博客_lr回归
来看参考文献[1]中两张直观经典的图:
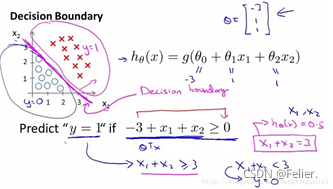
图1

图2
先来看图1所示的线性可分的情况,正、负样本在特征空间中可利用直线方程![]() 分割,这个直线方程又叫做边界函数,容易看到的结论是:
分割,这个直线方程又叫做边界函数,容易看到的结论是:
(1)对于正样本![]() 来讲,样本均处于直线上方,其满足
来讲,样本均处于直线上方,其满足![]() ;
;
(2)对于负样本![]() 来讲,样本均处于直线下方,其满足
来讲,样本均处于直线下方,其满足![]() ;
;
说个不算恰当但直观的认识就是,对于未知的样本![]() ,
,![]() 姑且可以认为
姑且可以认为![]() 的数值越远离零值,我们就有更大的信心认为该样本为正或负样本。反之亦反。
的数值越远离零值,我们就有更大的信心认为该样本为正或负样本。反之亦反。
说到这里,引入逻辑函数:
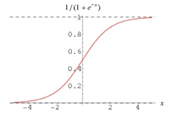
该函数的图像画出来就是下面的样子,在无穷的定义域上其取值从0到1,且当x的取值无穷大时,函数的数值也就无限的接近于1,即
。同理,
。
如何理解该逻辑函数,引用文献[3]的说法就是“一个事情发生的概率和影响这个事情发生的因素之间存在的一种关系”,其表现出来的特性就是,“因素的值无限放大或缩小的过程中,概率越接近于0,1时,因素对概率的影响越小”。
在说明了逻辑函数的后,前面的线性可分问题来定义如下预测函数似乎就不那么唐突了:
![]()
如令![]() ,把上式定义为:
,把上式定义为:
![]()
所述![]() 的意义就是,对于输入样本x被预测为正样本(y=1)的概率,即:
的意义就是,对于输入样本x被预测为正样本(y=1)的概率,即:
![]()
上述讨论针对的是二分类问题,自然是伯努利分布,因此被预测为负样本(y=0)的概率为:
![]()
下面讨论模型的训练过程。对于训练集的每一个训练样本(![]() ,yi)来说,该样本出现概率就能够计算为:
,yi)来说,该样本出现概率就能够计算为:
![]()
上式中的幂实际保证了两个P不同时取到,如样本(![]() ,1)的概率就是
,1)的概率就是![]() 。
。
假设各训练样本独立分布,则在n个训练样本上的似然估计函数为:
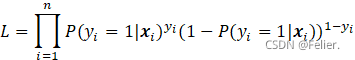
也即:
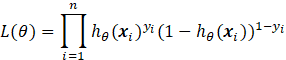
将上式取对数并不失其本身的单调性,故又有:
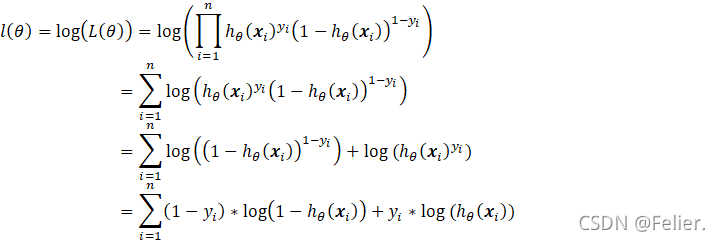
以上,![]() 就是逻辑回归模型的损失函数,接下来就是求解参数
就是逻辑回归模型的损失函数,接下来就是求解参数![]() 令
令![]() 最大,这等价于求解
最大,这等价于求解![]() 令
令![]() 最小,于是令
最小,于是令![]() ,这里求解
,这里求解![]() 的方法就是梯度下降法。
的方法就是梯度下降法。
参考文献[2],运用链式求导法则拿参数![]() 进行举例:
进行举例:
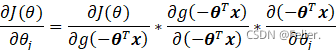
对于中间一项带入![]() 能够推出:
能够推出:
![]() ,
,
其实函数![]() 本身就具备
本身就具备![]() 的性质(有兴趣可以去研究下逻辑函数)。
的性质(有兴趣可以去研究下逻辑函数)。
为便于计算可以先求解![]() 的1个子项的梯度,它就等于:
的1个子项的梯度,它就等于:
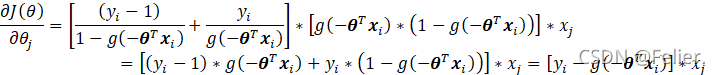
注意![]() 是向量
是向量![]() 的j分量,切勿混淆。
的j分量,切勿混淆。
那么![]() 的求和项的梯度为:
的求和项的梯度为:
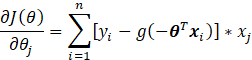
其中n为训练样本数量。
那么在n个训练样本上的参数![]() 更新公式为:
更新公式为:
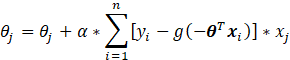
至此对![]() 的各个分量进行迭代求解即可,训练完成,至于向量化过程可见参考文献[1]。
的各个分量进行迭代求解即可,训练完成,至于向量化过程可见参考文献[1]。








 本文深入探讨了逻辑回归的概念,包括线性可分情况下的样本分割、逻辑函数的理解及其在预测概率中的应用。通过引入预测函数,解释了模型如何对二分类问题进行概率预测,并详细阐述了损失函数的构建和参数优化过程,特别是梯度下降法在参数更新中的作用。此外,还介绍了模型训练的关键步骤。
本文深入探讨了逻辑回归的概念,包括线性可分情况下的样本分割、逻辑函数的理解及其在预测概率中的应用。通过引入预测函数,解释了模型如何对二分类问题进行概率预测,并详细阐述了损失函数的构建和参数优化过程,特别是梯度下降法在参数更新中的作用。此外,还介绍了模型训练的关键步骤。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










