Canvas特效 旋转+轨迹详解

这一节我来给大家介绍canvas的旋转和轨迹

旋转

学过三角函数的都知道在圆上的点 x随着cosθ改变，y随着sinθ改变

x = cosθ, y = sinθ
范围是[-1,1]
如果我们想让一个点旋转的半径增大，那么只需要将其范围扩大即可
x = cosθ * s, y = sinθ *s

x = Math.cos(this.theta) * this.distance;
y = Math.sin(this.theta) * this.distance;

轨迹

如何向这样绘制一个轨迹呢？

如果你学过剪辑的话，就一定知道所谓重影分身不过是将上一帧的图像淡化保留
同样，我们只需要给小球在进行下一帧移动的时候加上一层“膜”

 ctx.fillStyle = 'rgba(255,255,255,0.1)';
 ctx.fillRect(0,0,canvas.width,canvas.height);

给每次小球要更新之前，让上一帧的小球变淡，这样就可以描绘出一条轨迹

所以我们绘制多个小球让其旋转，每个小球的颜色，半径，起始位置，与旋转点的距离都应不同

我们可以看出在移动鼠标的时候，小球下一帧是突然就刷出来
而不是演示中平滑的一条轨迹
所以我们不能直接用小球来绘制轨迹，应该采用线条
将小球填充色清除，记录小球上一帧的坐标，
将小球上一帧与当前帧两点连线

//ctx.fillStyle = this.color;
//ctx.arc(this.x, this.y, this.radius, 0, 2 * Math.PI);
//ctx.fill();
ctx.strokeStyle = this.color;
ctx.lineWidth = this.radius;
ctx.moveTo(lastPosition.x,lastPosition.y);
ctx.lineTo(this.x,this.y);
ctx.stroke();

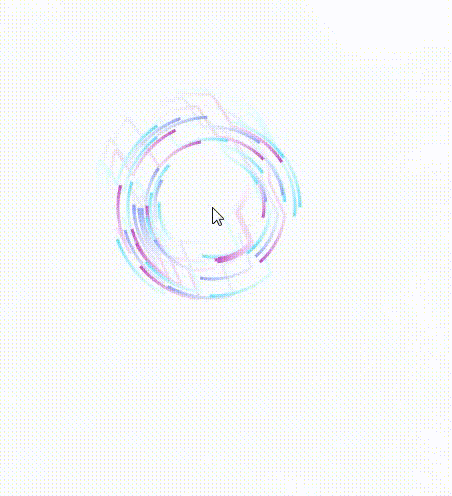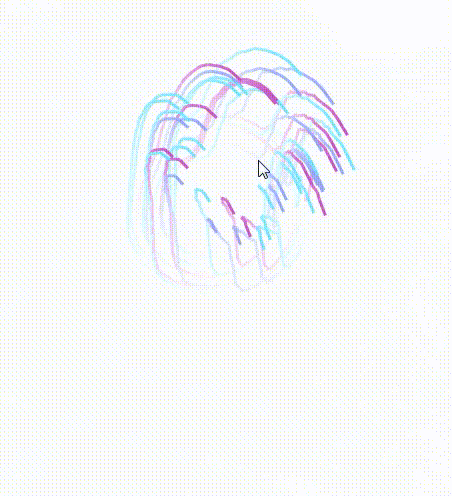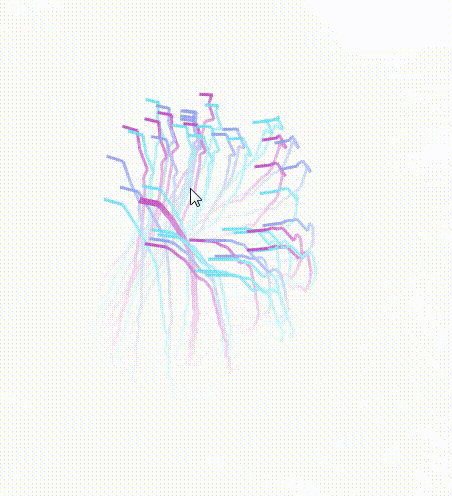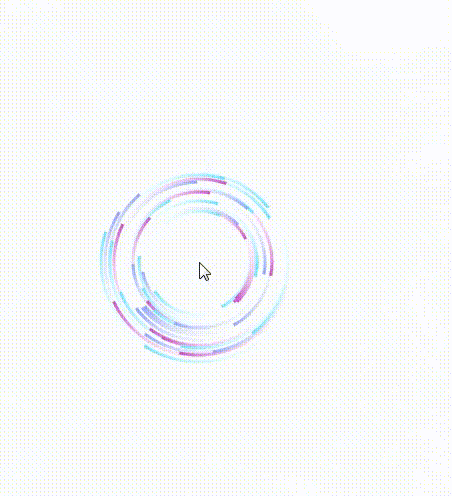
改为两点连线以后啊，我们发现移动鼠标的时候，线会扭曲，变得很丑

要改进很简单，我们需要引入一个步长的概念

假设你在正常情况下10s内走10米需要10步
现在让你在10s内走20步，你就需要步子迈小，步伐加快
同样，我们让小球从点A运动到另一个点B时 1单位时间打印一次
现在我们1单位时间打印n次，n越大 那么小球的轨迹就越多
所以
我们记录上一帧鼠标坐标，始终打印上一帧鼠标坐标
并且上一帧鼠标坐标更新机制为 （a+b）/ n

 // 拖拽效果
this.lastMouse.x += (mouse.x - this.lastMouse.x) / dragSpeed;
this.lastMouse.y += (mouse.y - this.lastMouse.y) / dragSpeed