7.6.1 用顶点表示活动的网络AOV
问题的提出
学生选修课程问题
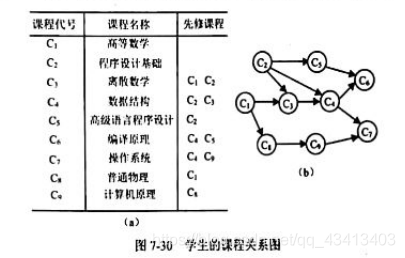
顶点,表示课程
有向弧,表示先决条件,若课程i是课程j的先决条件,则图中有弧<i,j>
学生应按怎样的顺序学习这些课程,才能无矛盾、顺利地完成学业——拓扑排序
相关定义
- 有向无环图(directed acycline graph),简称DAG图
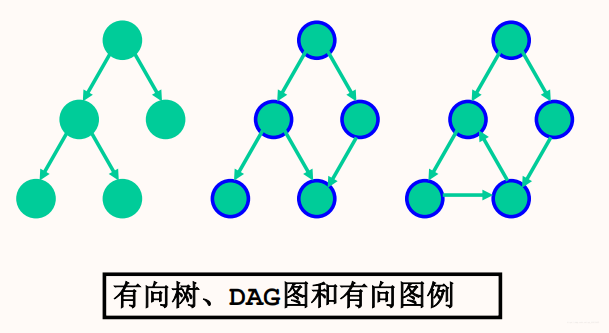
第二个图没有环,是DAG,第三个图有环,只能成为有向图 - 顶点表示活动(activity on vertices AOV)的网络
AOV是用以表示一个工程的有向图
图中的顶点表示一项子工程,即活动
弧表示两活动之间的先后次序
以计算机专业课程学习工程为例:
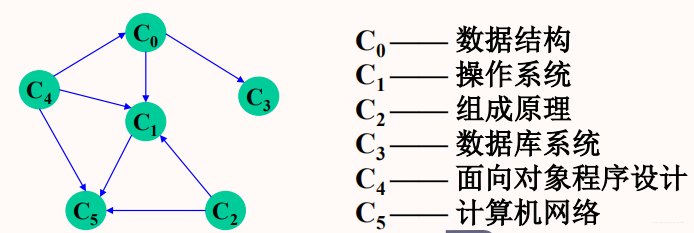
- 拓扑排序(Topological Sort):把AOV网络中各顶点按照它们相互之间的优先关系排列成一个线性序列的过程。
检测AOV网中是否存在环方法:对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV网必定不存在环。
(存在换的话,意味着某项活动的开始要以自己的完成作为先决条件,这显然是矛盾的)因此,对给定的AOV网络,必须先判断它是否存在有向环。
拓扑排序的方法:
(1)在有向图中选一个没有前驱的顶点且输出之
(2)从图中删除该顶点和所有以它为尾的弧(3)重复上述两步,直至全部顶点均已输出;或者当图中不存在无前驱的顶点为止。
注意:如果顶点有多个直接后继,排序结果通常不唯一。即,拓扑排序的结果唯一的情况是:每个顶点有唯一的前驱后继关系。
例如在下图中,存在两个拓扑有序序列,则说明拓扑排序不唯一。
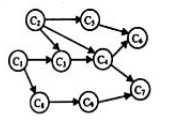
C1,C2,C3,C4,C5,C6,C8,C9,C7
C1,C8,C9,C2,C5,C3,C7,C4,C6
时间复杂度O(n+e)
拓扑排序算法
存储结构
AOV网络:邻接表
辅助变量:顶点入度数组InDegree[ ],记录各个顶点的入度
算法步骤
(1)建立入度为零的顶点栈;
(2)当入度为零的顶点栈为空时算法转步骤(6),否则继续步骤(3);
(3)入度为零的顶点栈中栈顶元素v出栈,并输出顶点v;
(4)从AOV网络中删去顶点v和所有从顶点v发出的弧<v , j >,并将顶点j的入度减一;
(5)如果顶点 j 入度减至0,则将该顶点进入入度为零的顶点栈;转步骤(2);
(6)如果输出顶点个数少于AOV网络的顶点个数,则输出网络中存在有向环的信息;算法结束。
算法实现
- 边节点类
template<class arcType> class ArcNode
{
public:
int vex;
ArcNode<arcType> *nextarc;
ArcNode()
{
nextarc=NULL;
}
ArcNode(int v,ArcNode<arcType> *next=NULL)
{
vex=v;
nextarc=next;
}
};
- 顶点节点类
#include "ArcNode.h"
template<class vertexType,class ArcType> class VertexNode
{
public:
vertexType vertex;
ArcNode<ArcType> *arcs;
VertexNode()
{
arcs=NULL;
}
VertexNode(vertexType v)
{
vertex=v;
arcs=NULL;
}
};
- 拓朴排序特殊邻接表(删除一些不必操作)实现
#define MaxVertexes 20
#include <iostream>
#include "VertexNode.h"
#include "ArcNode.h"
using namespace std;
template<class vertexType,class arcType> class VertexNode;
template<class arcType> class ArcNode;
class Graph
{
friend class VertexNode<int,int>;
friend class ArcNode<int>;
private:
VertexNode<int,int> *VertexesTable;
int *InDegree;
int CurrentNumVertexes;
int CurrentNumArcs;
//
int GetVertexPos(const int &v);
void Clear();
public:
Graph(int v[],int num=MaxVertexes);
~Graph();
void InsertVertex(int v);
void InsertArc(int head,int tail);
void Show()const;
void TopologicalOrder




 AOV网络,即顶点表示活动的网络,用于表示工程的有向图。拓扑排序是将这些网络中各顶点按照优先关系排列成线性序列的过程,用于解决如学生选课等有序问题。在有向无环图(DAG)中,通过算法判断是否存在环并进行排序。拓扑排序的时间复杂度为O(n+e),其中n是顶点数,e是边数。拓扑排序结果可能不唯一,取决于顶点的前驱和后继关系。常见实现方法包括使用栈或队列存储入度为0的顶点。
AOV网络,即顶点表示活动的网络,用于表示工程的有向图。拓扑排序是将这些网络中各顶点按照优先关系排列成线性序列的过程,用于解决如学生选课等有序问题。在有向无环图(DAG)中,通过算法判断是否存在环并进行排序。拓扑排序的时间复杂度为O(n+e),其中n是顶点数,e是边数。拓扑排序结果可能不唯一,取决于顶点的前驱和后继关系。常见实现方法包括使用栈或队列存储入度为0的顶点。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5569
5569

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








