最短路天梯赛题目

最新推荐文章于 2022-04-19 16:20:52 发布

原创最新推荐文章于 2022-04-19 16:20:52 发布 · 401 阅读

0 ·

CC 4.0 BY-SA版权

ACM 专栏收录该内容

19 篇文章

订阅专栏

博客围绕L2-001紧急救援题展开，指出这是一道图论题，考察最短路，属于Dijkstra算法模板题。它并非简单求最短路径路程和路径，还有附加条件。解题思路基本是Dijkstra模板，可维护各点救护人员数量和最短路径数目。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

L2

1.L2-001 紧急救援（25 分)

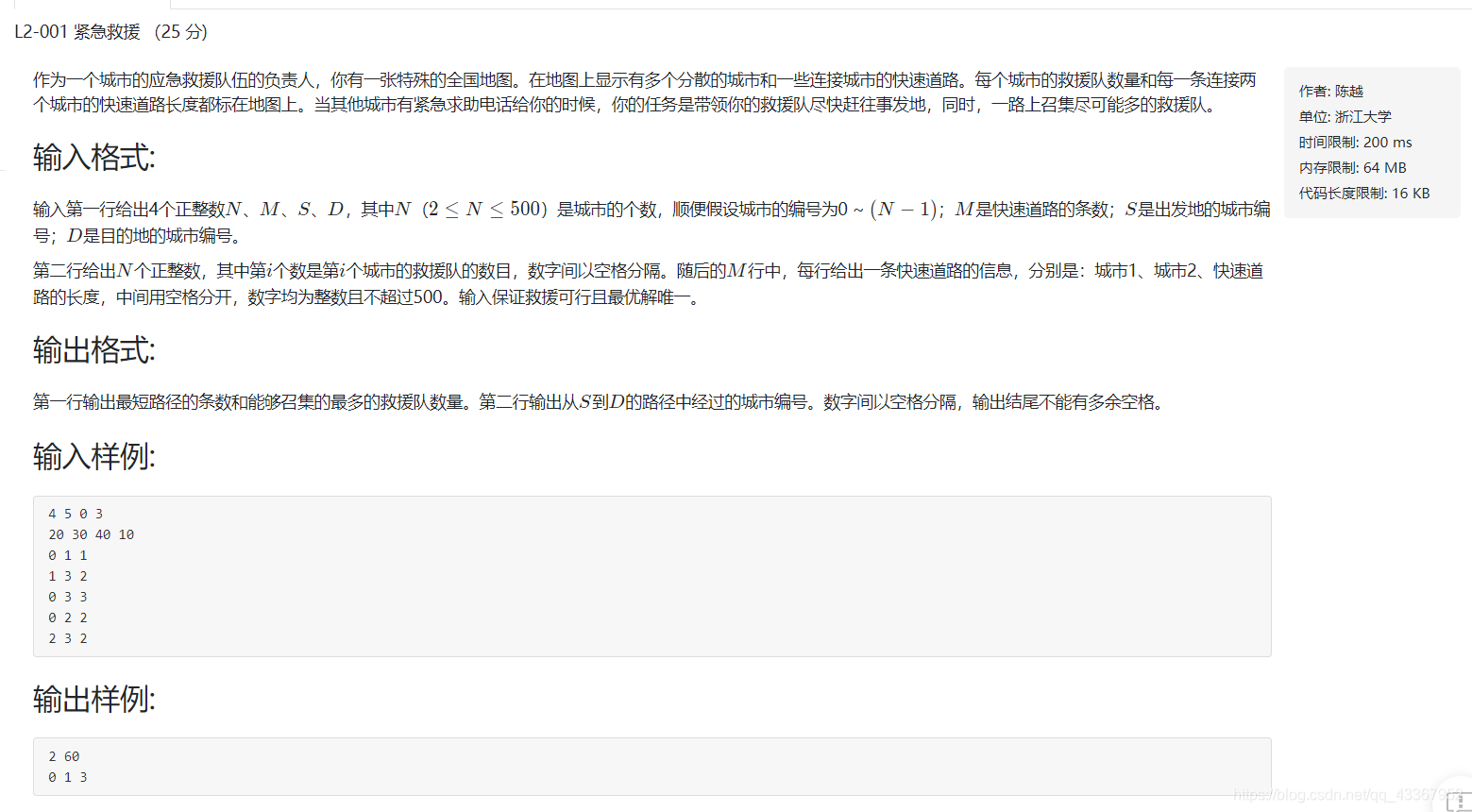
在这里插入图片描述
分析：
这道题是一道图论题，考察最短路，是一道Dijkstra算法的模板题。但他不是简单地考察输出最短路径路程和路径。还有一些附加条件，在多条件要求下去找合适的路径。
WA的原因：
思路：

基本上是Dijkstra模板。可以参考我的最短路问题博客
用数组维护各个点的救护人员数量和到这点的最短路径数目。这样维护下去，sum[ 终点 ] 就是从起点到终点的最大救护人员数目，ans [ 终点 ] 就是从起点到终点的最短路径的条数。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MA=1e3;
const int INF=1e8;
int city,road,st,en;//城市数，道路数，起点，终点
int dis[MA],cost[MA][MA],par[MA],ju[MA];//最短路长度，两点间距离，最短路中某一点的上一点，每个城市的救护人员数目，
int ans[MA],sum[MA];//到各点最短路径的条数，到各点救护人员的最大数。
bool vis[MA];
void Dijkstra()
{
    //初始化
    fill(dis,dis+city,INF);
    fill(par,par+city,INF);
    fill(vis,vis+city,false);
    for(int i=0;i<city;++i)
        par[i]=i;
    dis[st]=0;
    par[st]=st;
    ans[st]=1;
    while(1){
        int k=-1;
        for(int i=0;i<city;++i)
            if(!vis[i]&&(k==-1||dis[k]>dis[i]))k=i;
        if(k==-1)break;
        vis[k]=true;
        sum[st]=ju[st];
        for(int i=0;i<city;++i){
            if(cost[k][i]==INF)continue;
            if(dis[i]>dis[k]+cost[k][i]){
                par[i]=k;
                dis[i]=dis[k]+cost[k][i];
                sum[i]=sum[k]+ju[i];
                ans[i]=ans[k];
            }
            else if(dis[i]==dis[k]+cost[k][i]){
                ans[i]+=ans[k];
                if(ju[i]+sum[k]>sum[i]){
                    par[i]=k;
                    dis[i]=dis[k]+cost[k][i];
                    sum[i]=ju[i]+sum[k];
                }
            }
        }
    }
}
void print_tu(int s,int e)
{
    vector<int>path;
    for(int j=en;par[j]!=j;j=par[j]){
        path.push_back(j);
    }
    path.push_back(st);
   reverse(path.begin(),path.end());
   cout<<ans[e]<<" "<<sum[e]<<endl;
   for(vector<int>::iterator it=path.begin();it!=path.end();++it){
     if(it!=path.end()-1)
        cout<<*it<<" ";
     else cout<<*it<<endl;
   }
}
int main()
{
    cin>>city>>road>>st>>en;
    for(int i=0;i<city;++i)
        cin>>ju[i];
    for(int i=0;i<city;++i){
        for(int j=0;j<city;++j)
            cost[i][j]=INF;
    }
    int a,b,c;
    for(int i=0;i<road;++i){
        cin>>a>>b>>c;
        cost[a][b]=c;
        cost[b][a]=c;
    }
    Dijkstra();
    print_tu(st,en);
    return 0;
}