集成学习——Bagging

声明：

author:修远

此系列专栏为Datawhale下开源项目《李宏毅机器学习》集成学习的补充内容。作者水平有限，还望学习者批评指正。

目录

• github链接
• Bagging
• 那有没有可能样本始终没有被采样到
• Bagging为什么是低bias
• Bagging算法流程

1.链接

上一篇讲到了集成学习概述，接下来我们来学习Bagging

在李宏毅老师的集成学习课堂中，讲解的Bagging非常的好。

github链接：https://github.com/datawhalechina/leeml-notes

集成学习在线阅读地址：https://datawhalechina.github.io/leeml-notes/#/chapter38/chapter38

但是我仍有几个疑惑的问题，这篇博客主要解决这些问题

• 在Bagging的采样中，每个样本都被采样到了吗
• 为什么Bagging会降低variance(课程中用文字性的方法解释，这里我用具体的数学描述)
• Bagging算法流程

2.Bagging

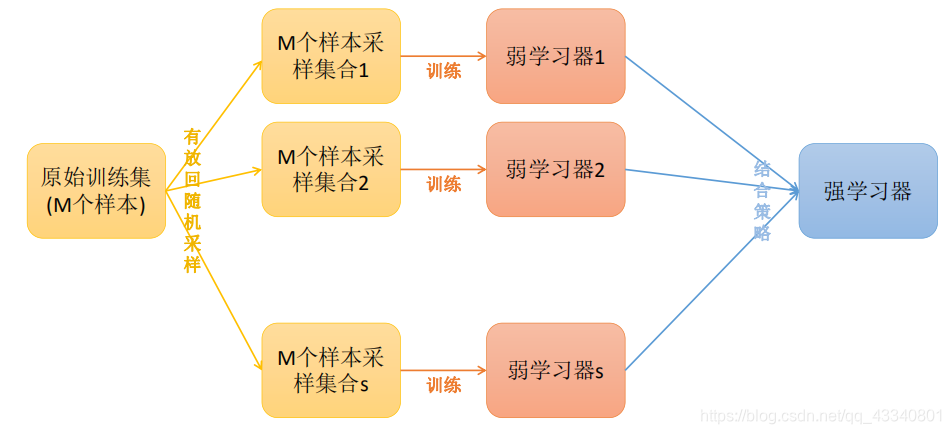
上图可以看出，Bagging的弱学习器是单独进行学习的，很容易并行处理，在不同的机器上运行。Bagging最大特点的采样方式为：“随机采样”

每轮从原始数据集中使用Bootstraping(有放回)的方法抽取n个训练样本，共进行K轮抽取，得到K个训练集(我们这里假设K个训练集之间是相互独立的，事实上不完全独立)

接下来每次使用一个训练集得到一个模型，k个训练集共得到k个模型。接着将得到的k个模型采用投票的方式得到分类结果；对于回归问题，计算上述模型的均值作为最后的结果

3.那有没有可能样本始终没有被采样到？

Bagging最大特点的采样方式为：“随机采样”，答案是有的。对于一个样本，它在某一次含m个样本的训练集的随机采样中，每次被采集到的概率是$\frac{1}{m}$，没有被采集到的概率为$1-\frac{1}{m}$。如果k次采样都没有被采样到的概率为$(1-\frac{1}{m}{)}^m$。当$k\to \infty$时，$(1-\frac{1}{m}{)}^m\to \frac{1}{e}\approx 0.368$。也就是说，在bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采样集采集中。

对于这部分大约36.8%的没有被采样到的数据，我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合，因此可以用来检测模型的泛化能力。

4.Bagging为什么是低bias

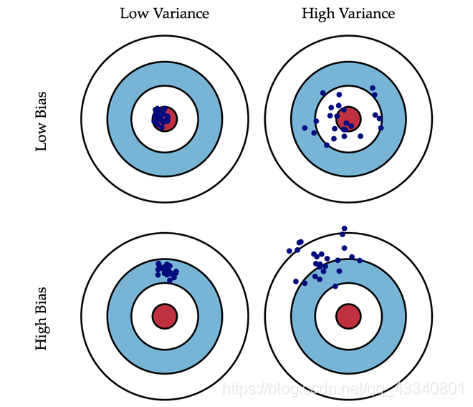
模型的偏差意味着：训练出来的模型在训练集上的准确度；模型的方差意味着：方差越大的模型越容易拟合。具体的内容可以查看李宏毅老师在“误差从哪来”这节课的讲解。

github在线阅读地址：https://datawhalechina.github.io/leeml-notes/#/chapter5/chapter5

假设在Bagging中，有m个模型，其中每个模型的权重为r(模型权重相等，均为$\frac{1}{m}$)，E代表期望，$\rho$基模型相关系数，
var代表方差，cov代表协方差。

$$E[F]=E[\sum _{i=1}^{m}r{f}_i]$$

$$=r\sum _{i=1}^{m}E$$