本文介绍了红黑树，它是一种特殊的二叉查找树，每个节点有红或黑两种颜色，具有五条特性以保证相对平衡。还阐述了红黑树的基本操作，包括左旋、右旋、插入和删除，详细说明了插入和删除操作在不同情况下的修复方法及代码实现。
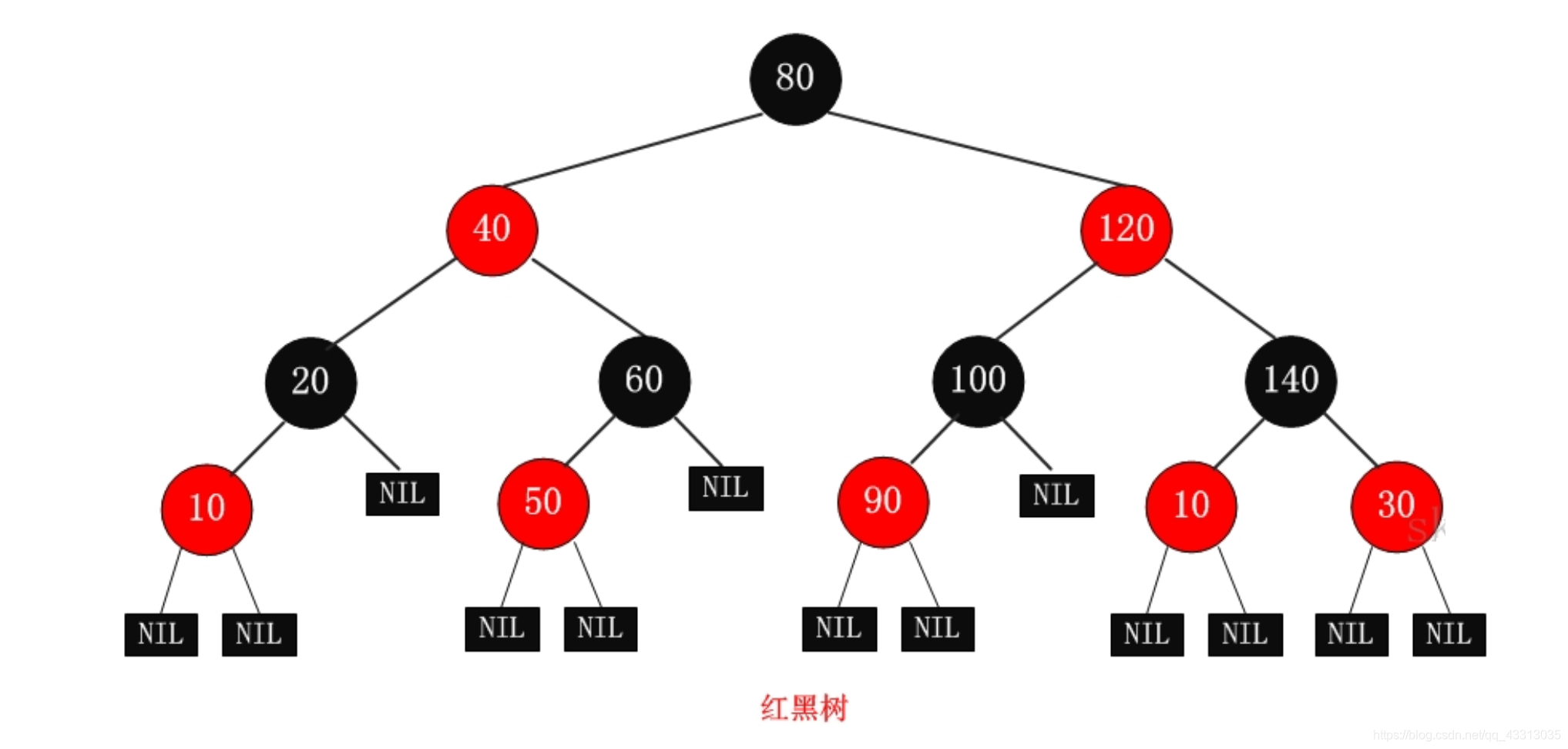
红黑树的简单介绍
R-B Tree，全称是Red-Black Tree，又称为“红黑树”，它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色，可以是红(Red)或黑(Black)。
红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
注意：
- 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
- 特性(5)，确保没有一条路径会比其他路径长出2倍。因而，红黑树是相对是接近平衡的二叉树。
红黑树的数据结构定义
template<typename T>
class RBTree
{
public:
RBTree() :_root(nullptr) {}
private:
struct RBNode
{
RBNode(T data = T(),
Color color = BLACK,
RBNode *parent = nullptr)
:_data(data)
, _left(nullptr)
, _right(nullptr)
, _parent(parent)
, _color(color)
{}
T _data;
RBNode *_left;
RBNode *_right;
RBNode *_parent;
Color _color;
};
Color color(RBNode *node)
{
return node == nullptr ? BLACK : node->_color;
}
void setColor(RBNode *node, Color color)
{
node->_color = color;
}
RBNode* left(RBNode *node)
{
return node->_left;
}
RBNode* right(RBNode *node)
{
return node->_right;
}
RBNode* parent(RBNode *node)
{
return node->_parent;
}
RBNode *_root; // 指向红黑树的根节点
};
红黑树的基本操作
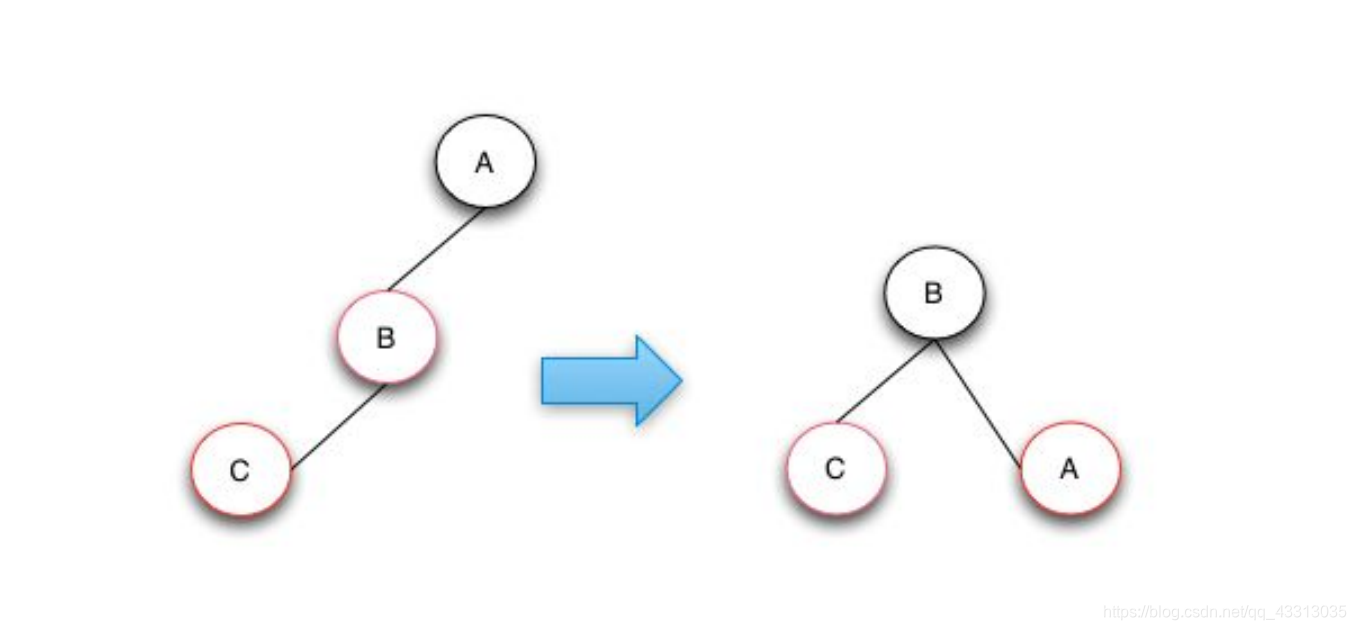
左旋
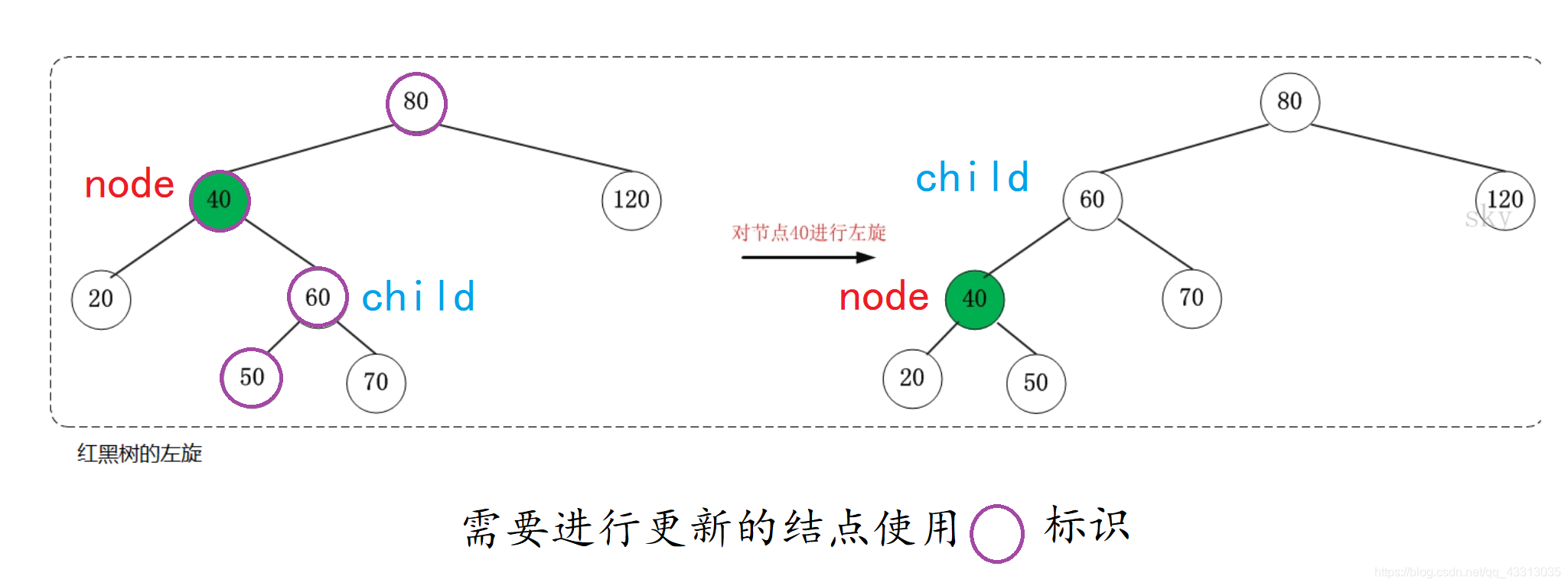
void leftRotate(RBNode *node)
{
RBNode *child = node->_right;
child->_parent = node->_parent;
if (node->_parent == nullptr)
{
_root = child;
}
else
{
if (node->_parent->_left == node)
{
node->_parent->_left = child;
}
else
{
node->_parent->_right = child;
}
}
node->_right == child->_left;
if (child->_left != nullptr)
{
child->_left->_parent = node;
}
node->_parent = child;
}
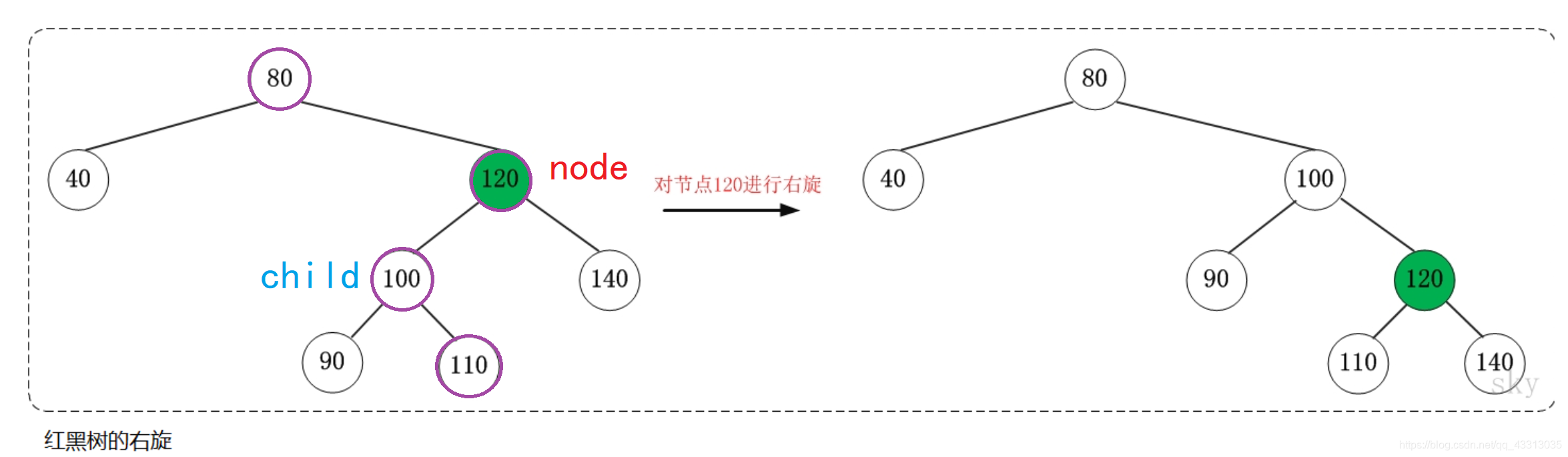
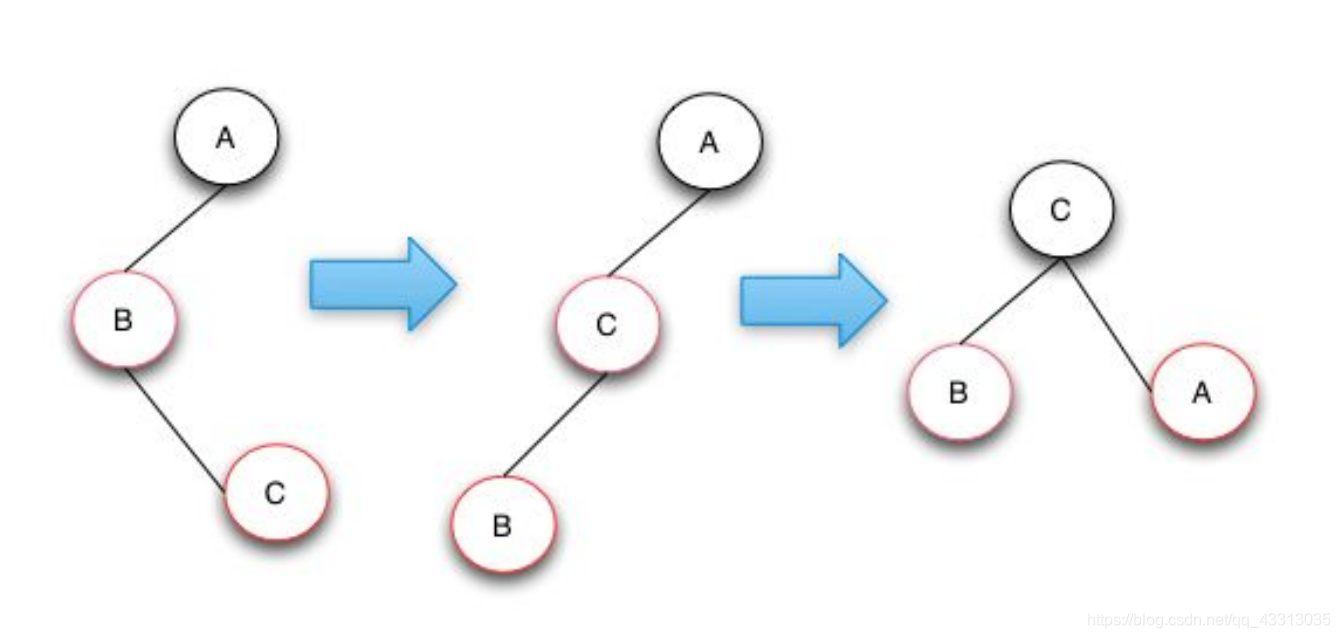
右旋
红黑树的插入
新插入的节点是红色的，插入修复操作如果遇到父节点的颜色为黑则修复操作结束。
也就是说，只有在父节点为红色节点的时候是需要插入修复操作的
插入修复操作分为以下三种情况：
- 叔叔节点为红色
- 叔叔节点为黑色或者为空，且祖父节点、父节点和新节点处于一条斜线上
- 叔叔节点为黑色或者为空，且祖父节点、父节点和新节点不处在一条斜线上
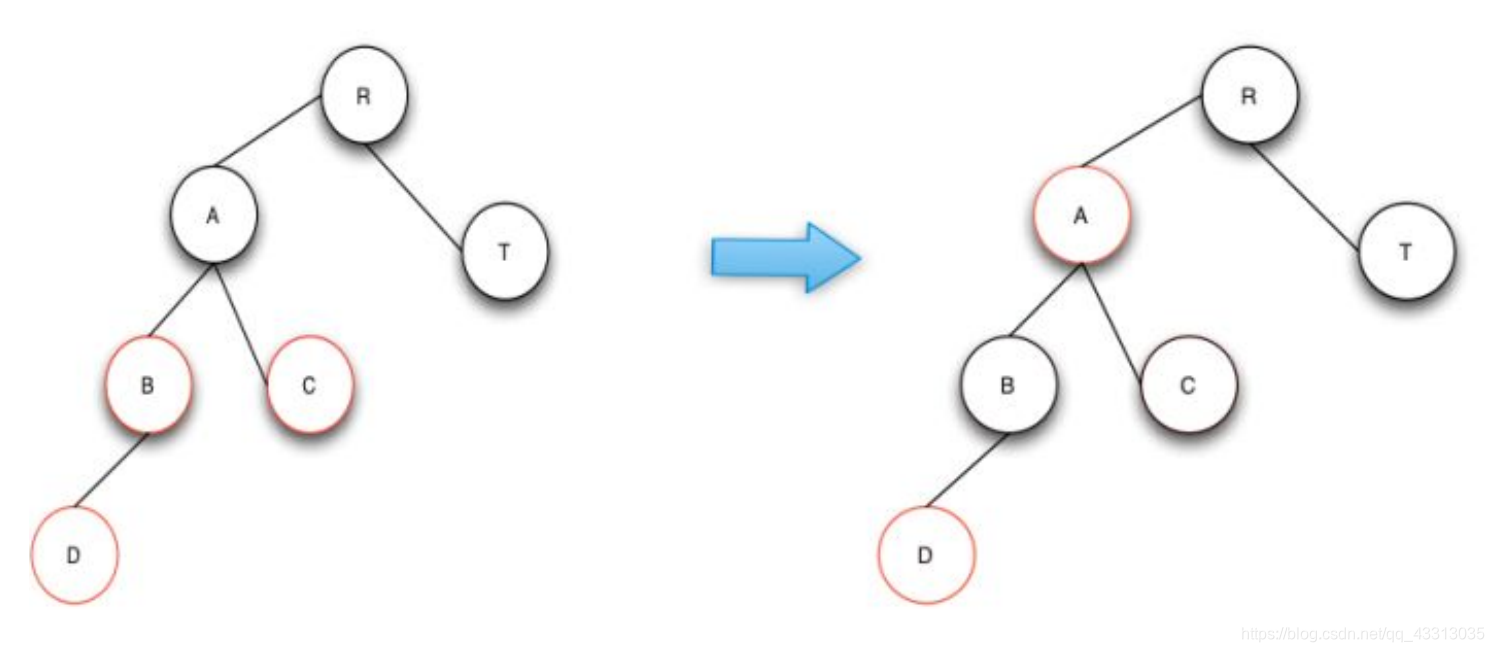
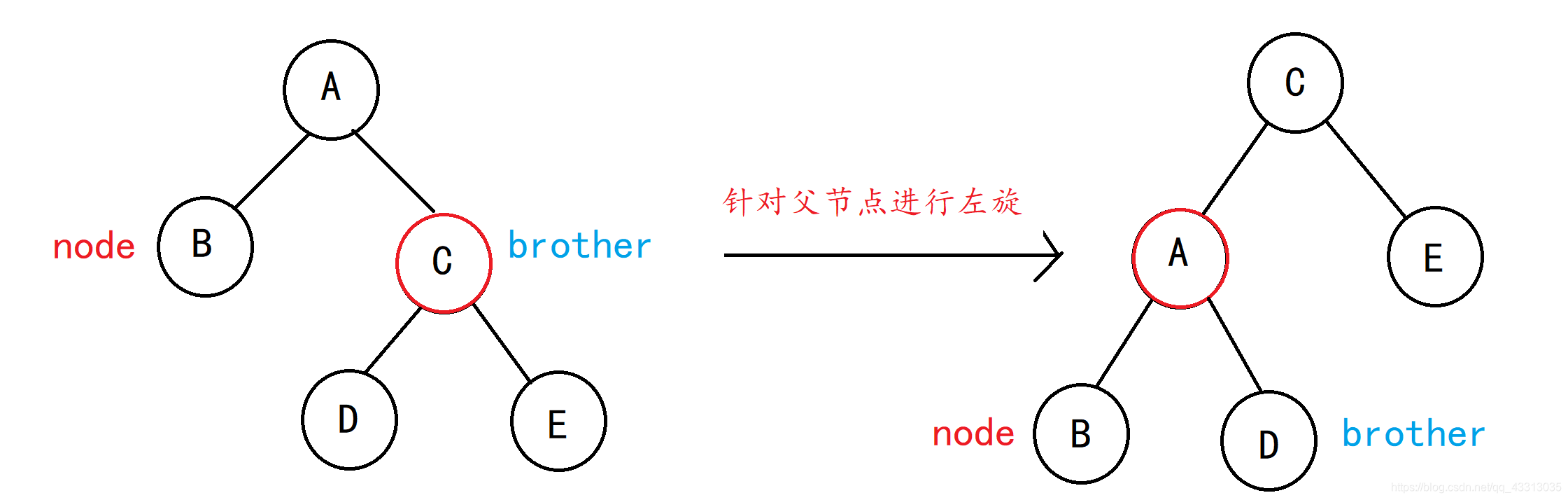
情况1：祖先置红色，叔叔和父亲置黑色，指针指向祖先，继续判断，直到父节点为黑色节点终止，祖先若是根结点，直接置为黑色。
情况2：父亲节点置为黑色，祖父节点置为红色，针对祖父节点进行右旋
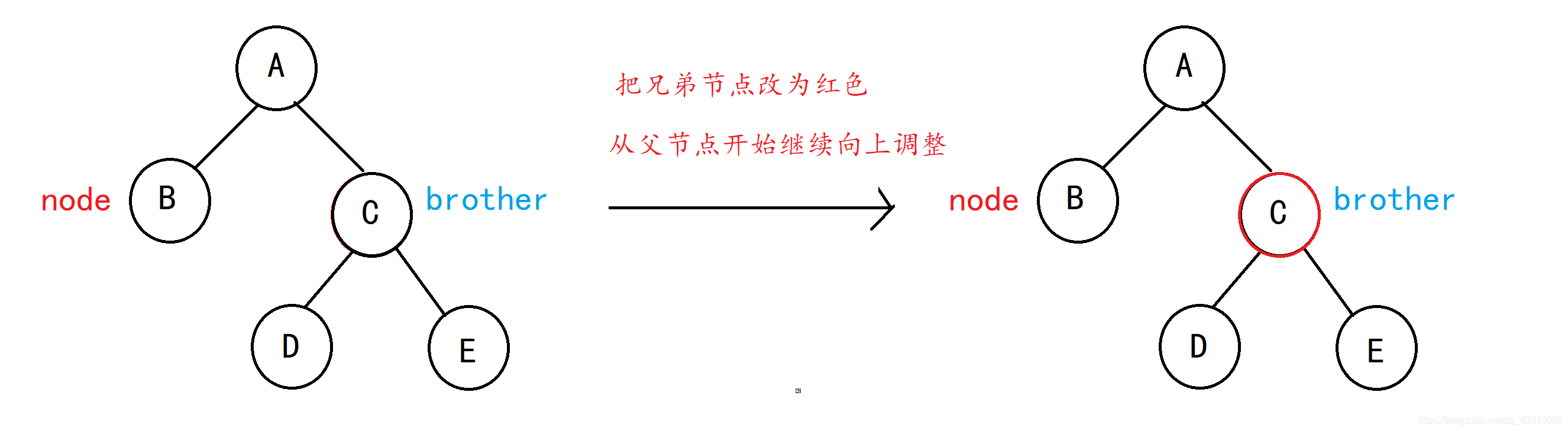
情况3：首先针对父节点进行左旋操作，将会变为情况2
插入操作实现代码
void insert(const T &val)
{
if (_root == nullptr)
{
_root = new RBNode(val, BLACK);
return;
}
RBNode *parent = nullptr;
RBNode *cur = _root;
while (cur != nullptr)
{
parent = cur;
if (cur->_data > val)
{
cur = cur->_left;
}
else if (cur->_data < val)
{
cur = cur->_right;
}
else
{
return;
}
}
RBNode *node = new RBNode(val, RED, parent);
if (val < parent->_data)
{
parent->_left = node;
}
else
{
parent->_right = node;
}
if (color(parent) == RED)
{
fixAfterInsert(node);
}
}
插入修复操作
void fixAfterInsert(RBNode *node)
{
while (color(parent(node)) == RED)
{
if (left(parent(parent(node))) == parent(node))
{
// 插在了祖先节点的左子树当中
RBNode *uncle = right(parent(parent(node)));
/*
* 情况1：叔叔节点为红色
* 首先将父亲节点和叔叔节点都置为黑色，祖父节点置为红色
* 将指针指向祖父节点再进行判断
* 直到节点的父节点为黑色或到达根节点，直接置为黑色
*/
if (color(uncle) == RED)
{
setColor(parent(node), BLACK);
setColor(uncle, BLACK);
setColor(parent(parent(node)), RED);
node = parent(parent(node));
}
else
{
/*
* 情况3:叔叔节点为黑色或者为空，且祖父节点、父节点和新节点不处在一条斜线上
* 首先针对父节点进行左旋操作，将会变为情况2
*/
if (node == right(parent(node)))
{
node = parent(node);
leftRotate(node);
}
/*
* 情况2：叔叔节点为黑色或者为空，且祖父节点、父节点和新节点处于一条斜线上
* 将父亲节点置为黑色，祖父节点置为红色
* 再针对祖父节点进行右旋
*/
setColor(parent(node), BLACK);
setColor(parent(parent(node)), RED);
rightRotate(parent(parent(node)));
break;
}
}
else
{
// 插在了祖先节点的右子树当中
RBNode *uncle = left(parent(parent(node)));
// 情况1
if (color(uncle) == RED)
{
setColor(parent(node), BLACK);
setColor(uncle, BLACK);
setColor(parent(parent(node)), RED);
node = parent(parent(node));
}
else
{
// 情况3
if (node == left(parent(node)))
{
node = parent(node);
rightRotate(node);
}
// 情况2
setColor(parent(node), BLACK);
setColor(parent(parent(node)), RED);
leftRotate(parent(parent(node)));
break;
}
}
}
setColor(_root, BLACK);
}
红黑树的删除
情况一：兄弟结点是红色
情况二：兄弟结点为黑色并且其左右孩子也是黑色
情况三：兄弟结点为黑色并且其右孩子为红色左孩子为黑色
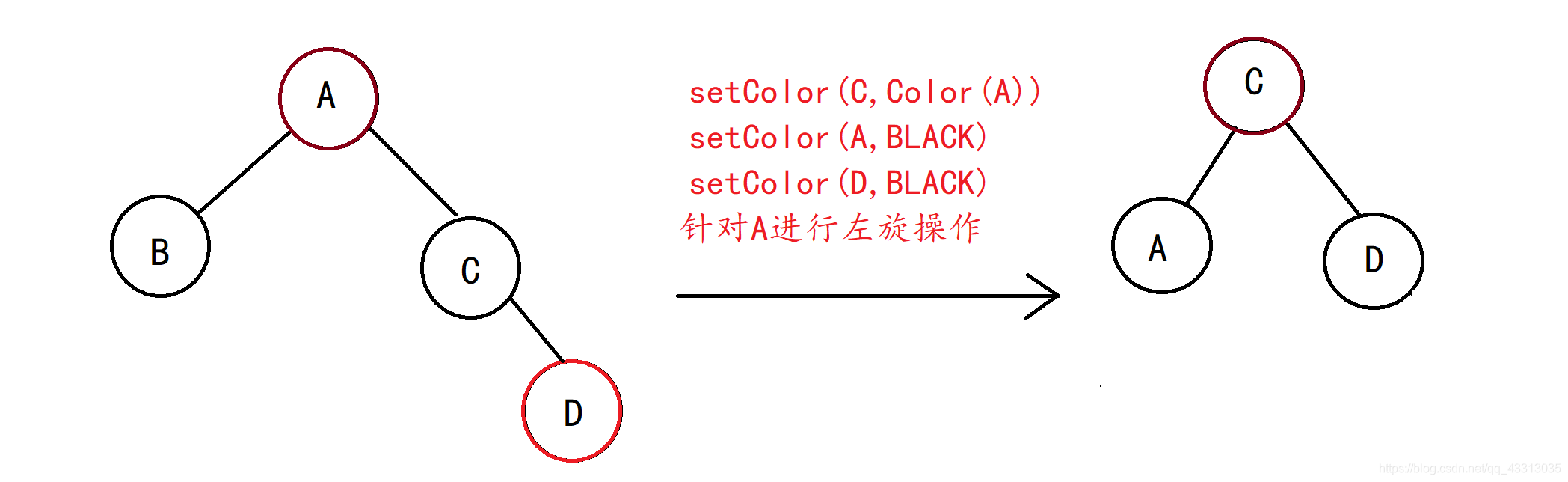
情况四：兄弟结点为黑且左孩子为红色，右孩子可为任意颜色
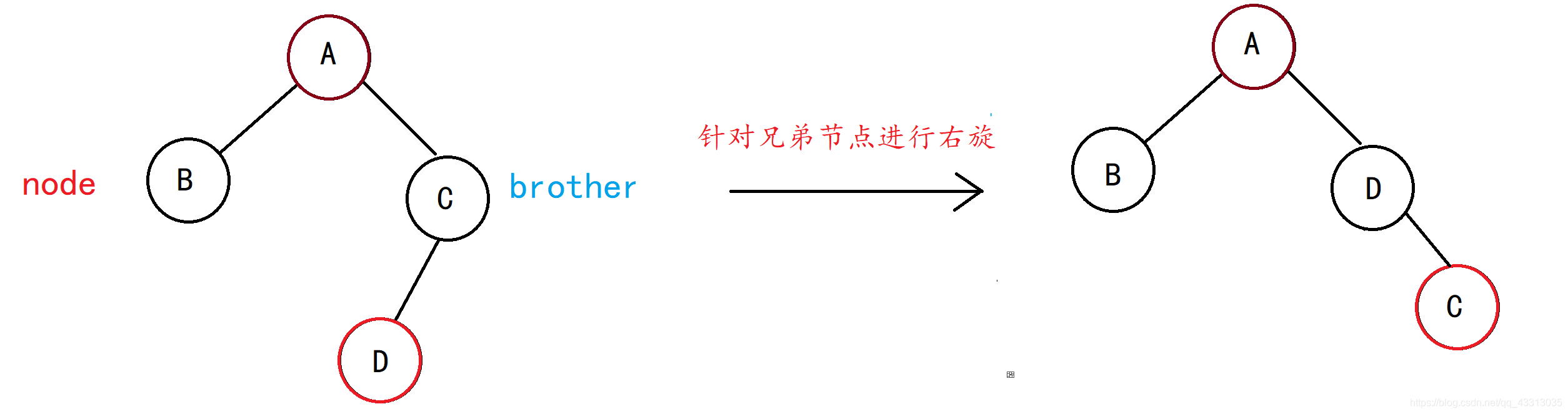
删除代码实现：
void remove(const T &val)
{
if (_root == nullptr)
return;
RBNode *parent = nullptr;
RBNode *cur = _root;
while (cur != nullptr)
{
if (cur->_data > val)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_data < val)
{
parent = cur;
cur = cur->_right;
}
else
{
break;
}
}
if (cur == nullptr)
return;
//待删除节点有两个孩子的情况
if (cur->_left != nullptr && cur->_right != nullptr)
{
RBNode *old = cur;
parent = cur;
cur = cur->_left;
while (cur->_right != nullptr)
cur = cur->_right;
old->_data = cur->_data;
}
//只有一个孩子或者没有孩子的情况
RBNode *child = cur->_left;
if (child == nullptr)
child = cur->_right;
//只有一个孩子的情况
if (child != nullptr)
{
child->_parent = cur->_parent;
if (cur->_parent == nullptr)
{
_root = child;
}
else
{
if (cur->_parent->_left == cur)
{
cur->_parent->_left = child;
}
else
{
cur->_parent->_right = child;
}
}
Color color = color(cur);
delete cur;
//待删除节点是黑色，需要进行调整
if (color == BLACK)
{
fixAfterRemove(child);
}
}
//待删除节点没有孩子
else
{
//待删除节点为根节点
if (parent(cur) == nullptr)
{
_root = nullptr;
}
//待删除节点不是根节点
else
{
//待删除节点的颜色是黑色，需要进行调整
if (color(cur) == BLACK)
{
fixAfterRemove(cur);
}
/*
* 待删除节点为其父节点的左孩子
* 将其父节点的左孩子置为nullptr
*/
if (left(parent(cur)) == cur)
{
cur->_parent->_left = nullptr;
}
//否则将其父节点的有孩子置为nullptr
else
{
cur->_parent->_right = nullptr;
}
delete(cur);
}
}
}
删除修复调整
void fixAfterRemove(RBNode *node)
{
//待调整节点颜色为黑色
while (Color(node) == BLACK)
{
//待调整节点为其父节点的左孩子
if (left(parent(node)) == node)
{
//记录兄弟节点
RBNode *brother = right(parent(node));
//如果兄弟节点为红色
if (color(brother) == RED)
{
setColor(brother, BLACK);//兄弟节点置为黑色
setColor(parent(node), RED);//父节点置为红色
leftRotate(parent(node));//针对父节点进行左旋
brother = right(parent(node));//更新兄弟节点
}
/*
* 兄弟节点为黑色，且兄弟节点的两个孩子都是黑色
*/
if (color(left(brother)) == BLACK
&& color(right(brother) == BLACK)
{
setColor(brother, RED);//把兴地节点置为红色
node = parent(node);//从父节点继续向上调整
}
else
{
//兄弟节点为黑色且兄弟节点的左孩子为红色，右孩子为黑色
if (color(right(brother)) != RED)
{
setColor(brother, RED);//把兄弟节点置为红色
setColor(left(brother), BLACK);//把兄弟节点的左孩子置为黑色
rightRotate(brother);//针对兄弟节点进行右旋
brother = right(parent(node));//更新兄弟节点
}
//兄弟节点为黑色且兄弟节点右孩子为红色，左孩子为任意颜色
setColor(brother, color(parent(node)));//将兄弟节点颜色置为夫系欸但的颜色
setColor(parent(node), BLACK);//将父节点的颜色置为黑色
setColor(right(brother), BLACK);//将兄弟节点的右孩子置为黑色
leftRotate(parent(node));//针对根节点进行左旋
node = _root;
}
}
else //调整父节点的右孩子
{
//兄弟结点在父节点左边
RBNode *brother = left(parent(node));
//情况一：兄弟结点是红色
if (color(brother) == RED)
{
setColor(brother, BLACK);
setColor(parent(node), RED);
rightRotate(parent(node));
brother = left(parent(node));
}
//情况二：兄弟结点为黑色并且其左右孩子也是黑色
if (color(left(brother)) == BLACK
&& color(right(brother) == BLACK)
{
setColor(brother, RED);
node = parent(node);
}
else
{
//情况三：兄弟结点为黑色并且其右孩子为红色左孩子为黑色
if (color(left(brother)) != RED)
{
setColor(brother, RED);
setColor(right(brother), BLACK);
leftRotate(brother);
brother = left(parent(node));
}
//情况四：兄弟结点为黑且左孩子为红色，右孩子可为任意颜色
setColor(brother, color(parent(node)));
setColor(parent(node), BLACK);
rightRotate(parent(node));
}
}
}
/*
* 删除黑色节点后，其孩子节点是红色，上面循环无法进入
* 我们直接将孩子结点直接调成黑色，即可保持黑色节点数量不变
* 删除黑色节点后，其孩子节点是黑色，但是向上回溯的时候，
* 遇到红色节点，直接将其改成黑色节点即可。
*/
setColor(node, BLACK);
}
扫一扫
1027
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
