Java实现归并排序

归并排序算法思想

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。，通过将大问题简化即可得到最终的答案。

归并排序图例：

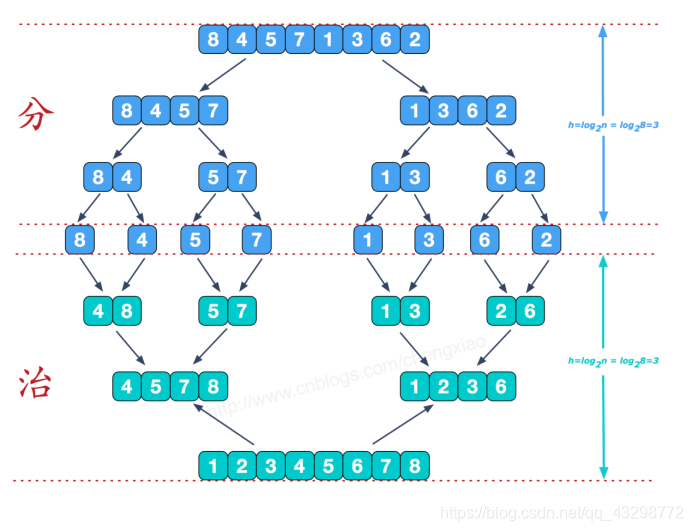
1. 如上图所示，刚开始有一组乱序的数字，需要对他们进行排序，可将原始的长数组从中一分为二，得到两个较小的数字数组
2. 给短数组排序要比给长数组排序简单些，所以为了能再简单，将得到的较短数组再次一分为二，直到数组中只含有一个数字， 此时，我们可以认为单个数字在他们各自的数组中是有序的
3. 之后将两个有序的数组合并到一起并整理为有序数组，之后再次逐层向上合并整理，直到合并成为一个原始长度的数组，所得数组为最终的有序数组

在写归并排序时，可先从将单个数字后向一个序列合并的过程即“归”的过程入手，以上述图示为例，假设我们所有的数据已经合并完成，现在只剩下两个4长的有序数组，我们现在要做的就是将这两个有序数组合并为最后的原始长度的有序数组

归并排序代码实现

我们将合并过程写到一个方法之中，格式如下：

private static void mergeMethod(int[] arr, int startIndex, int centerIndex, int endIndex) {

}

方法参数需要：要排序的数组名、开始索引、结束索引和中间索引

参数详解：

1. 中间索引用来将数组分为逻辑上的两个数组，（其实在将原始数组逐层一分为二最终让每个数组中只含有一个元素的时候，这些数组在物理空间上还是在一起的，但在逻辑上是分开的，所以需要中间索引来在逻辑上对他们进行分割，让他们在逻辑上是分开的）
2. 之后左边数组以整体开始索引为开始索引，以中间索引为结束索引，
3. 右边数组以中间索引为开始索引，以整体结束索引为结束索引，
4. 通过上述参数，即可将数组分为逻辑上的两个数组，
5. 在将数组分为逻辑上的两个数组后，即可定义临时数组，之后用索引依次比较两个数组中的各个数据，将小的数字放到临时数组中，比较完成后，得到的数组就是最终排好顺序的从小到大的数字数组

既然需要使用开始索引、结束索引和中间索引，就需要在方法内部定义三个整型变量来存放这些索引，所以需要执行下面的代码：

int[] tempArr = new int[endIndex - startIndex + 1];     
//定义临时数组，根据结束索引和开始索引来确定临时数组的长度，因为数组长度可能不一样，如果是两个4长数组合并，则临时数组长度为8
int i = startIndex;    //定义开始索引
int j = centerIndex + 1;    //定义中间索引
int index = 0;           //定义临时数组索引

在定义完成需要使用到的一些变量后就可以逐个比较小数组中的元素，将小的数字放到临时数组中，代码如下：

while (i <= centerIndex && j <= endIndex) { //确保小数组的索引不会越界
        //如果第一个序列的第一个元素，小于等于第二个序列的第一个元素
        if (arr[i] <= arr[j]) {
            tempArr[index] = arr[i]; //把小的元素，放到临时数组中
            i++; //递增一下索引，下次对比第后面的元素
        } else {
            tempArr[index] = arr[j];
            j++;   //递增一下索引，下次比较后面的元素
        }
        index++; //记得让临时数组的的索引递增，这样才能不断地给临时数组中补充数值
}

但会存在下面的情况：

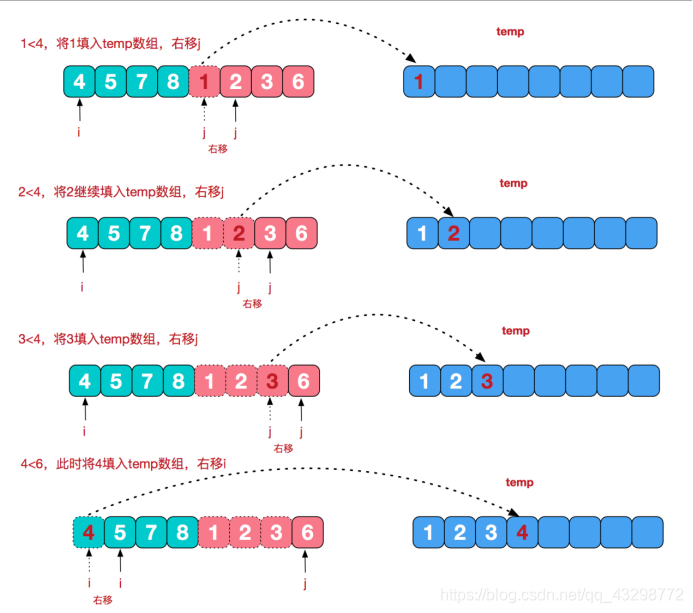
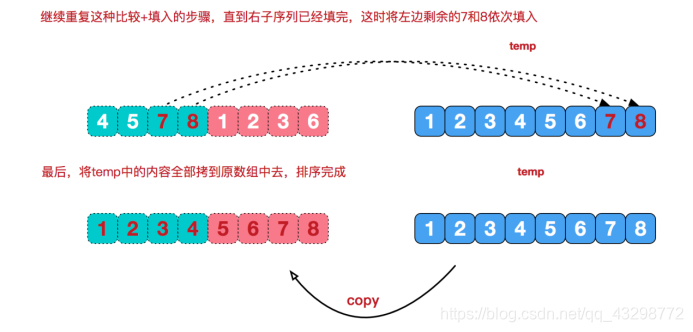
从上图可以看出，最终右边的数组会先被比较完，在右边的数组全部被放入到临时数组后，左边还剩余7和8，此时上面提到的循环会跳出，因为两边总会有个数组存在索引越界，从而跳出上面提到的循环；所以还需要一个循环来将剩余的变量放入临时数组，代码如下：

while (i <= centerIndex) {
      tempArr[index] = arr[i]; //把小的元素，放到临时数组中
      i++; //递增一下索引，下次对比第二个元素
      index++;//临时数组的的索引递增
}

该循环是左边的数组剩余，右边剩余的话循环代码如下：

while (j <= endIndex) {
        tempArr[index] = arr[j];
        j++;
        index++;
}

所有代码就实现了对两个数组的合并，之后将临时数组中的各个元素依次拷贝到在原始数组所在位置即可

for (int k = 0; k < tempArr.length; k++) {
        //注意这里k要加上起始索引
        arr[k + startIndex] = tempArr[k];    //k一定要加上起始索引，否则之后赋给原始数组的值会将之前的值覆盖掉，排序会出错
}

通过上述所有代码就完成了归即合并的过程，将合并方法定义完成后，就需要定义拆分方法，因为要先将原始数组逐层拆分，拆分到每个数组中只含有一个元素，才能进行合并，拆分代码如下：

private static void chaiFen(int[] arr, int startIndex, int endIndex) {
    //计算中间索引
    int centerIndex = (startIndex + endIndex) / 2;
    if (startIndex < endIndex) { //递归拆分
        //拆分左边
        chaiFen(arr, startIndex, centerIndex);
        //拆分右边
        chaiFen(arr, centerIndex + 1, endIndex);
        //拆分完成后归并
        mergeMethod(arr, startIndex, centerIndex, endIndex);
    }

}

拆分通过递归实现，所以归并排序完成

归并排序代码示例：

 public class MyTest {
    public static void main(String[] args) {
      int[] arr = {1, 3, 6, 9, 2, 4, 7, 8, 10, 0, 20, 100, 89, 30, 26};
      chaiFen(arr, 0, arr.length - 1);
      System.out.println(Arrays.toString(arr));
    }

    private static void chaiFen(int[] arr, int startIndex, int endIndex) {
      int centerIndex = (startIndex + endIndex) / 2;
      if (startIndex < endIndex) {
        chaiFen(arr, startIndex, centerIndex);
        chaiFen(arr, centerIndex + 1, endIndex);
        mergeMethod(arr, startIndex, centerIndex, endIndex);
      }
    }


    private static void mergeMethod(int[] arr, int startIndex, int centerIndex, int endIndex) {
      int[] tempArr = new int[endIndex - startIndex + 1];
      int i = startIndex;
      int j = centerIndex + 1;
      int index = 0;
      while (i <= centerIndex && j <= endIndex) {
        if (arr[i] <= arr[j]) {
            tempArr[index] = arr[i];
            i++;
        } else {
            tempArr[index] = arr[j];
            j++;
        }
        index++;
      }
      
      while (i <= centerIndex) {
        tempArr[index] = arr[i]; 
        i++; 
        index++;
      }
      
      while (j <= endIndex) {
        tempArr[index] = arr[j];
        j++;
        index++;
      }
      
      for (int k = 0; k < tempArr.length; k++) {
        arr[k + startIndex] = tempArr[k];
      }
   }
}

以上就是关于归并排序的讲解