MLP（多层感知机）虚战1

最新推荐文章于 2024-06-10 23:10:36 发布

占疏

最新推荐文章于 2024-06-10 23:10:36 发布

阅读量1k

点赞数 16

文章标签：人工智能

本文链接：https://blog.youkuaiyun.com/qq_43242266/article/details/135416627

版权

使用Keras实现MLP

前两节地址：

优快云 matplotlib 虚战1-优快云博客（数据的获取在这有说明）

数据预处理虚战1-优快云博客优快云

数据预处理的最后一步：将数据集分为训练数据集、测试数据集和校验数据集。

训练数据集：神经网络将基于此子数据集进行训练。

测试数据集：基于此子数据集对模型进行最终的评估。

验证数据集：提供无偏差数据以帮助我们进行超参数的调节（调节隐藏层的个数）
数据预处理虚战1-优快云博客 preprocess的代码在这

import numpy as np
np.random.seed(16)
import matplotlib
matplotlib.use("TkAgg")
from utils import preprocess
import pandas as pd
from sklearn.model_selection import train_test_split
import numpy as np
np.random.seed(16)


df = pd.read_csv('diabetes.csv')

# Perform preprocessing and feature engineering
df = preprocess(df)

# Split the data into a training and testing set
X = df.loc[:, df.columns != 'Outcome']
y = df.loc[:, 'Outcome']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

这里只把数据简单分为训练数据集和测试数据集

X = df.loc[:, df.columns != 'Outcome'] # 获取全部的行，除了Outcome列的所有列。

y = df.loc[:, 'Outcome'] # 获取全部的行，只要Outcome列。

记住Outcome是目标结果，有糖尿病或者没有糖尿病，即1或者0。

train_test_split() 函数完成这个分割过程，80%作为训练数据集、 20%作为测试数据集。

模型结构

MLP是一种前馈神经网络，至少有一个隐藏层，且每层均通过一个非线性激活函数。这种多层神经网络结构和非线性激活函数使得MLP可以生成非线性的决策边界。

输入层：输入层的每个节点表示一个特征。

隐藏层：对应一个激活函数，该层最终输出结果由激活函数、权重和偏差决定。

激活函数：需要为每一层选择一个激活函数

这里使用，修正线性单元（Rectified Linear Unit,ReLU）和 sigmoid 激活函数作为激活函数。

ReLU常常作为中间层的激活函数（非输出层），是深度神经网络的默认的激活函数。

ReLU函数仅仅考虑原始X中非负的部分，并将负数部分替换为0。

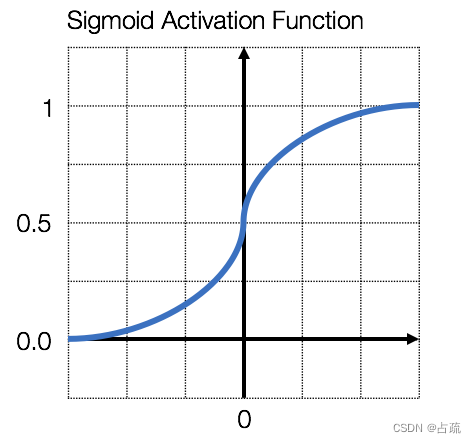
sigmoid激活函数将输出值的范围压缩至0到1之间。sigmoid激活函数接收一个输入值并输出一个二元的分类结果（1或0）。

建模

使用Keras构建模型

通过将层堆叠起来的方法在Keras中创建一个神经网络：

activation='relu'

1.先创建一个Sequential()类

model = Sequential()

2.然后创建第一个隐藏层，该隐藏层包含32个节点，输入的维度input_dim是8，因为该数据集有8个特征。只有第一个隐藏层需要指明输入维度，后面的隐藏层会自动处理。

第一个隐藏层中节点的个数，比如这里设置的32，是一个超参数（需要调试才得出来的数），这里人为的选择32作为节点个数，该数据集较简单，该变量产生的影响并不大。

activation='relu' 选择ReLU作为激活函数

3.添加第二个隐藏层

4.添加输出层，输出层只有一个节点，因为处理的是二元分类问题，激活函数使用的是sigmoid函数，它将输出结果压缩至0~1（二元输出）。

模型编译

model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

训练模型之前，先定义训练过程的参数，通过compile()方法完成。

训练过程中的3个参数：

优化器：这里使用adam优化器

损失函数：使用二元交叉熵（binary_crossentropy）作为损失函数，因为这是一个二元分类问题

评估标准：使用准确率（即正确分类的样本比例）作为模型性能的评估标准。

模型训练

model.fit(X_train, y_train, epochs=200)

调用fit函数训练我们之前训练的模型，进行200轮，可以看到每一轮训练的情况，损失减少，准确度提高。这是学习算法根据训练数据在持续不断更新MLP的权重和偏差。这里的准确率指的是基于训练数据集的准确率。

结果分析

MLP模型已经完成训练，可通过基于测试准确率、混淆矩阵（confusion matrix）和受试者操作特征曲线（Receiver Operating Characteristic,ROC）来评估模型的性能。

# Results - Accuracy
scores = model.evaluate(X_train, y_train, verbose=False)
print("Training Accuracy: %.2f%%\n" % (scores[1]*100))
scores = model.evaluate(X_test, y_test, verbose=False)
print("Testing Accuracy: %.2f%%\n" % (scores[1]*100))

训练数据集和测试数据集上的模型准确率。

可以看到训练数据集的准确率是会比测试数据集的准确率高很多的，因为本来就是在训练数据集上训练出来的。基于测试数据计算出的准确率是我们评估模型在真实环境中应用准确率的标准，这是数据是模型未曾训练过的。

混淆矩阵是一个很有用的可视化工具。

真阴性：实际分类为阴性（没有糖尿病）而模型预测结果也是阴性（未患糖尿病）

假阴性：实际分类为阳性（有糖尿病）而模型预测结果是阴性（未患糖尿病）

真阳性：实际分类为阳性（患糖尿病）而模型预测结果为阳性（患糖尿病）

假阳性：实际分类为阴性（未患糖尿病）而模型预测结果为阳性（患糖尿病）

真阳性和真阴性的数量越多就好，而假阳性和假阴性的数量越少越好。

# Results - Confusion Matrix
y_test_pred = model.predict_classes(X_test)
c_matrix = confusion_matrix(y_test, y_test_pred)
ax = sns.heatmap(c_matrix, annot=True, xticklabels=['No Diabetes', 'Diabetes'], yticklabels=['No Diabetes', 'Diabetes'], cbar=False, cmap='Blues')
ax.set_xlabel("Prediction")
ax.set_ylabel("Actual")
plt.show()
plt.clf()

sns.heatmap()绘制热度图

c_matrix ：数据

cmap：定义热度图的配色板

annot：是否显示数值注释

cbar：删除seaborn中默认的条带，设置cbar=False。

xticklabels、yticklabels 刻度标签

ROC曲线

将真阳性率（TPR）作为y轴，假阳性率（FPR）作为x轴。

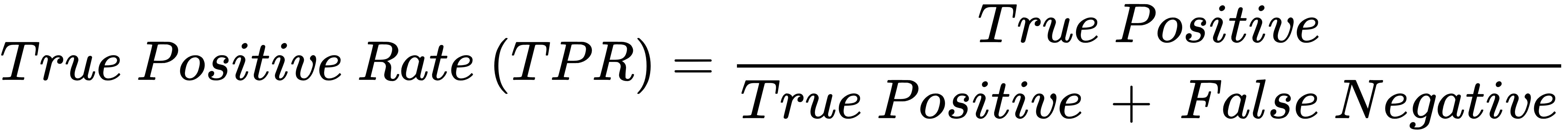
在分析ROC曲线时，通过曲线下方面积（Area Under the Curve,AUC）可以对该曲线的模型进行性能评估。

AUC大，表示模型能够更准确地区分不同分类

AUC小，表示模型做出的预测准确率不高，预测结果常有错

落在对角线上的ROC表示模型预测准确率并不高于随机预测的。

scikit-learn 提供了roc_curve类来帮我们绘制ROC曲线。

# Results - ROC Curve
y_test_pred_probs = model.predict(X_test)
FPR, TPR, _ = roc_curve(y_test, y_test_pred_probs)
plt.plot(FPR, TPR)
plt.plot([0,1],[0,1],'--', color='black') #diagonal line  对角线
plt.title('ROC Curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()
plt.clf()

结果：

可以看出，该模型预测效果不错。

全部代码：

import matplotlib
matplotlib.use("TkAgg")
from utils import preprocess
import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve
from keras.models import Sequential
from keras.layers import Dense
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(16)


df = pd.read_csv('diabetes.csv')


# Perform preprocessing and feature engineering
df = preprocess(df)

# Split the data into a training and testing set
X = df.loc[:, df.columns != 'Outcome']
y = df.loc[:, 'Outcome']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# Build neural network in Keras
model = Sequential()
model.add(Dense(32, activation='relu', input_dim=8))
model.add(Dense(16, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=200, verbose=False)

# Results - Accuracy
scores = model.evaluate(X_train, y_train, verbose=False)
print("Training Accuracy: %.2f%%\n" % (scores[1]*100))
scores = model.evaluate(X_test, y_test, verbose=False)
print("Testing Accuracy: %.2f%%\n" % (scores[1]*100))

# Results - Confusion Matrix
y_test_pred = model.predict_classes(X_test)
c_matrix = confusion_matrix(y_test, y_test_pred)
ax = sns.heatmap(c_matrix, annot=True, xticklabels=['No Diabetes', 'Diabetes'], yticklabels=['No Diabetes', 'Diabetes'], cbar=False, cmap='Blues')
ax.set_xlabel("Prediction")
ax.set_ylabel("Actual")
plt.show()
plt.clf()

# Results - ROC Curve
y_test_pred_probs = model.predict(X_test)
FPR, TPR, _ = roc_curve(y_test, y_test_pred_probs)
plt.plot(FPR, TPR)
plt.plot([0,1],[0,1],'--', color='black') #diagonal line
plt.title('ROC Curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.show()
plt.clf()

参考：

python使用seaborn画热力图中设置colorbar图例刻度字体大小_seaborn 设置colorbar刻度-优快云博客

Python可视化 | Seaborn5分钟入门(六)——heatmap热力图 - 知乎 (zhihu.com)

python 神经网络项目实战