一本通：1259：【例9.3】求最长不下降序列

最新推荐文章于 2025-06-24 19:52:18 发布

流水落花，白云出岫

最新推荐文章于 2025-06-24 19:52:18 发布

阅读量1.7k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：一本通文章标签：动态规划递归一本通

本文链接：https://blog.youkuaiyun.com/qq_43210798/article/details/99674371

本文介绍了一种使用动态规划求解最长不下降序列的方法，通过定义状态转移方程f[i]，考虑当a[i]小于等于a[j]时如何更新序列长度。最终，最长的序列长度就是所有f[i]中的最大值。文章还提到，输出序列时可以采用递归思想，从最后一个记录的下标向前输出。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：1259：【例9.3】求最长不下降序列(http://ybt.ssoier.cn:8088/problem_show.php?pid=1259)

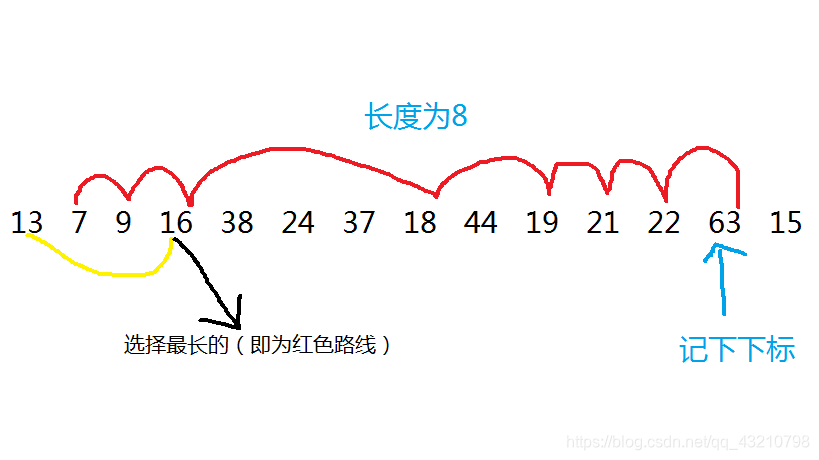
在这里插入图片描述

思路：

令f[i]为从1到i的最长不下降序列长度

假设a[i]<=a[j]，那么就构成了一个不下降序列（不用相邻）

假如加上这个数，序列比原来更长，那么就加上；若序列没有原来长，那么就不变

所以状态转移方程为f[i]=f[j]+1或f[i]不变

最后输出的长度即为所有长度中最长的

输出序列时，从记下的最后一个下标往前输出（用递归思想）

代码：

#include<iostream>
using namespace std;

void out(int x,int m[],int k);
int a[201];

int main()
{
	int n,i,j,f[201]={0},p[201]={0},maxn=0,l;  //令f[i]为从1到i的最长不下降序列长度  
	cin>>n;
	for(i=1;i<=n;i++)
	{
		cin>>a[i];
		f[i]=1; //每一个数最少都有本身长度
	}
	for(i=1;i<n;i++)
	{
		for(j=i+1;j<=n;j++)
		{
			if(a[j]>=a[i]&&f[j]<f[i]+1)
			{
				f[j]=f[i]+1;
				p[j]=i; //记下当前序列中上一个数的下标
			}
		}
	}
	for(i=1;i<=n;i++)
	{
		if(maxn<f[i])
		{
			maxn=f[i];
			l=i; //记下序列中最后一个数的下标
		}
	}
	cout<<"max="<<maxn<<