LeetCode 221.最大正方形

最新推荐文章于 2025-01-03 20:58:06 发布

原创最新推荐文章于 2025-01-03 20:58:06 发布 · 241 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #动态规划 #数据结构 #java

Leetcode 专栏收录该内容

29 篇文章

订阅专栏

这篇博客介绍了LeetCode 221题的解决方案，通过动态规划方法寻找矩阵中能构成的最大正方形的边长。文章强调了状态定义、转移方程以及如何优化成一维数组实现，详细解释了如何利用前一行数据来更新当前行，最终找到最大正方形的边长并返回其平方作为答案。

LeetCode 221.最大正方形

确定状态：
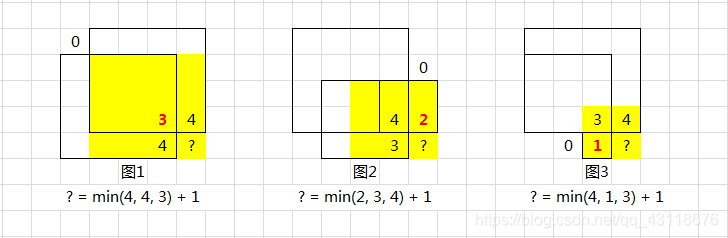
引用自LeetCode
正方形的理解：
如图所示，对于每个位置(i,j)，其能确定最大的正方形边长，其实是(i-1,j-1),(i-1,j),(i,j-1)三个位置的最大正方形的边长最小值（类比于：木桶的短板理论，AOE图中的关键路径）。
状态： 设f[i][j]为所在位置最大正方形的边长。
转移方程：
f[i][j]=min{f[i-1][j-1],f[i-1][j],f[i][j-1]}.
初始条件和边界
保证数组索引不越界，遍历从下标1开始。
最后答案是边长的平方

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m=matrix.length;
        
        if(m==0)
            return 0;
        int n=matrix[0].length;
        int [][]f=new int[m+1][n+1];
        int res=0;
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(matrix[i-1][j-1]=='1'){ 
                    f[i][j]=1+Math.min(f[i-1][j-1],Math.min(f[i][j-1],f[i-1][j]));
                    res=Math.max(res,f[i][j]);
                }
            }
        }
        return res*res;
   }
}

优化：
观察转移方程：
f[i][j]=min{f[i-1][j-1],f[i-1][j],f[i][j-1]}，我们发现可以只用一维数组实现：
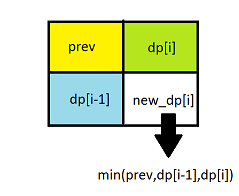
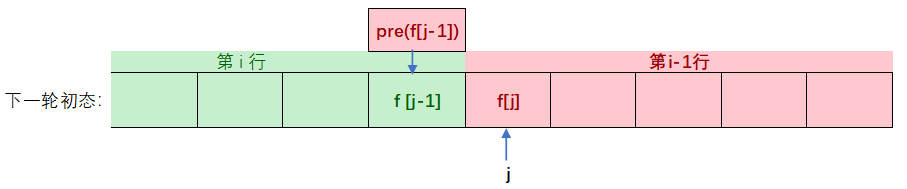
在这里插入图片描述

红色表示上一行的数据，绿色表示该行数据
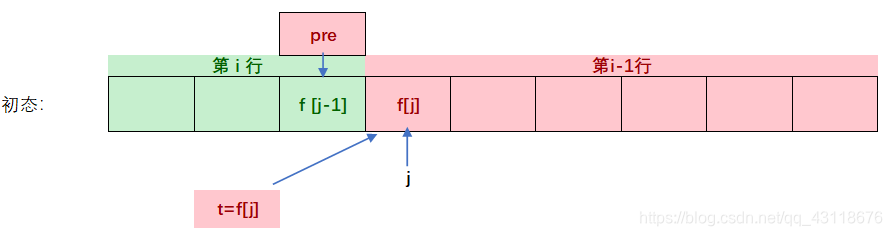
在这里插入图片描述
因为计算后上一行f[j]将被覆盖,需要t用来保存上一行f[j]的值。
这个t就成为下一轮的pre，之前二维数组中的f[i-1][j-1]

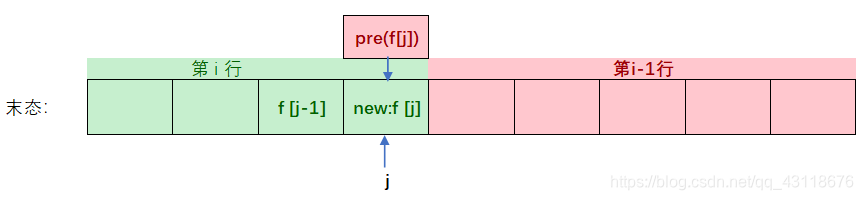
进入下一次循环，j++之后：

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m=matrix.length;
        if(m==0)
            return 0;
        int n=matrix[0].length;
        int []f=new int[n+1];
        int res=0,t=0,pre=0;
        int i,j;
        for(i=1;i<=m;i++)
        {
            for(j=1;j<=n;j++)
            {
                t=f[j];
                if(matrix[i-1][j-1]=='1'){ 
                    f[j]=1+Math.min(f[j-1],Math.min(pre,f[j]));
                    res=Math.max(res,f[j]);
                }
                else
                    f[j]=0;
                pre=t;
            }
        }
        return res*res;
    }
}