算法笔记——数学相关
个人算法笔记:戳我qwq
高精度
- 核心思想:字符串模拟数组,实现大整数(大于long long的范围)运算。
- 应用范围:
1.
l
o
n
g
l
o
n
g
long long
longlong存不下
Q
A
Q
QAQ
QAQ;
2.模拟运算(高精度本来就是模拟);
- 读入:
void init(int a[])
{
string s;
cin>>s;
a[0]=s.lenth();
for(int i=1;i<=a[0];++i)
a[i]=s[a[0]-i]-'0';
}
- 进位,借位处理
加法进位:
c[i]=a[i]+b[i];
if(c[i]>=10)
{
c[i]%=10;
++c[i+1];
}
减法借位:
if(a[i]<b[i])
{
--a[i+1];
a[i]+=10;
}
c[i]=a[i]-b[i];
乘法进位:
c[i+j-1]=a[i]*b[j]+x+c[i+j-1];
x=c[i+j-1]/10;
c[i+j-1]%=10;
商和余数:视情况而定
- 代码
高精度加法(模板:A+B problem 高精)
#include<cstdio>
#include<cstring>
using namespace std;
char a1[505],b1[505];
int len1,len2,len3;
int a[505],b[505],c[505];
int main()
{
scanf("%s%s",a1,b1);
len1=strlen(a1);
len2=strlen(b1);
for(int i=0;i<len1;++i)
a[len1-i]=a1[i]-'0';
for(int i=0;i<len2;++i)
b[len2-i]=b1[i]-'0';
len3=1;
int x=0;
while(len3<=len1||len3<=len2)
{
c[len3]=a[len3]+b[len3]+x;
x=c[len3]/10;
c[len3]%=10;
len3++;
}
c[len3]=x;
if(c[len3]==0)len3--;
for(int i=len3;i>=1;--i)
printf("%d",c[i]);
return 0;
}
高精度减法(模板:高精度减法)
#include<cstdio>
#include<cstring>
#define maxn 10005
using namespace std;
char a1[maxn],b1[maxn],m[maxn];
int len1,len2,len3,flag;
int a[maxn],b[maxn],c[maxn];
int main()
{
scanf("%s%s",a1,b1);
if(strlen(a1)<strlen(b1)||(strlen(a1)==strlen(b1)&&strcmp(a1,b1)<0))
{
flag=1;
strcpy(m,a1);
strcpy(a1,b1);
strcpy(b1,m);
}//交换数组
len1=strlen(a1);
len2=strlen(b1);
for(int i=0;i<len1;++i)a[len1-i]=a1[i]-'0';
for(int i=0;i<len2;++i)b[len2-i]=b1[i]-'0';
len3=1;
int x=0;
while(len3<=len1||len3<=len2)
{
if(a[len3]<b[len3])
{
a[len3]+=10;
a[len3+1]--;
}//借位
c[len3]=a[len3]-b[len3];
len3++;
}
while(c[len3]==0&&len3>1)len3--;
if(len3==1&&c[1]==0)
{
printf("0");
return 0;
}
if(flag)
printf("-");
for(int i=len3;i>=1;--i)
printf("%d",c[i]);
return 0;
}
高精度乘法(模板:A*B problem)
#include<cstdio>
#include<cstring>
#define maxn 5005
using namespace std;
char a1[maxn],b1[maxn];
int len1,len2,len3;
int a[maxn],b[maxn],c[maxn];
int main()
{
scanf("%s%s",a1,b1);
len1=strlen(a1);
len2=strlen(b1);
for(int i=0;i<len1;++i)a[len1-i]=a1[i]-'0';
for(int i=0;i<len2;++i)b[len2-i]=b1[i]-'0';
for(int i=1;i<=len1;++i)
{
int x=0;
for(int j=1;j<=len2;++j)
{
c[i+j-1]+=a[i]*b[j]+x;
x=c[i+j-1]/10;
c[i+j-1]%=10;
}
c[i+len2]=x;
}
len3=len1+len2;
while(c[len3]==0&&len3>1)len3--;
for(int i=len3;i>=1;--i)
printf("%d",c[i]);
return 0;
}
高精度除法(高精除以低精)(模板:A/B problem)
#include<cstdio>
#include<cstring>
#define maxn 10005
using namespace std;
int len1,len2;
int b,a[maxn],c[maxn];
char a1[maxn];
int main()
{
scanf("%s%d",a1,&b);
len1=strlen(a1);
for(int i=0;i<len1;++i)a[i+1]=a1[i]-'0';
int x=0;
for(int i=1;i<=len1;++i)
{
c[i]=(x*10+a[i])/b;
x=(x*10+a[i])%b;
}
len2=1;
while(c[len2]==0&&len2<len1)len2++;
for(int i=len2;i<=len1;++i)
printf("%d",c[i]);
return 0;
}
高精度除法(高精除以高精)(模板:A/B problem II)
#include<cstdio>
#include<cstring>
#include<iostream>
#define maxn 1005
using namespace std;
int a[maxn],b[maxn],c[maxn];
void read(int a[])
{
string s;
cin>>s;
a[0]=s.length();
for(int i=1;i<=a[0];++i)
a[i]=s[a[0]-i]-'0';
}//读入
void print(int a[])
{
if(a[0]==0)
{
printf("0\n");
return;
}
for(int i=a[0];i>0;--i)
printf("%d",a[i]);
printf("\n");
return;
}//输出
int cmp(int a[],int b[])
{
if(a[0]>b[0])return 1;
if(a[0]<b[0])return -1;
for(int i=a[0];i>0;--i)
{
if(a[i]>b[i])return 1;
if(a[i]<b[i])return -1;
}
return 0;
}//比较数组a,b的大小
void jian(int a[],int b[])
{
int flag;
flag=cmp(a,b);
if(flag==0)
{
a[0]=0;
return;
}//相等
if(flag==1)
{
for(int i=1;i<=a[0];++i)
{
if(a[i]<b[i])
{
a[i+1]--;
a[i]+=10;
}//借位
a[i]-=b[i];
}
while(a[0]>0&&a[a[0]]==0)a[0]--;
return;
}
}//模拟减法
void numcpy(int p[],int q[],int del)
{
for(int i=1;i<=p[0];++i)
q[i+del-1]=p[i];
q[0]=p[0]+del-1;
}//数组复制
void chugao(int a[],int b[],int c[])
{
int tmp[maxn];
c[0]=a[0]-b[0]+1;
for(int i=c[0];i>=1;--i)
{
memset(tmp,0,sizeof(tmp));
numcpy(b,tmp,i);
while(cmp(a,tmp)>=0)
{
c[i]++;
jian(a,tmp);
}
}
while(c[0]>0&&c[c[0]]==0)c[0]--;
return;
}
int main()
{
read(a);read(b);
chugao(a,b,c);
print(c);
print(a);//输出余数
return 0;
}
乘法逆元
- 概念
联系小学学过的倒数, x ∗ 1 x = 1 x*\frac{1}{x}=1 x∗x1=1,在 c + + c++ c++中如果贸然直接除以 x x x,可能会出问题。然而如果对于一个数 x x x,若存在另一个数 x − 1 x^{-1} x−1,使 x ∗ x − 1 x*x^{-1} x∗x−1模上一个数 m o d mod mod等于1,那么这个数 x − 1 x^{-1} x−1就是 x x x的逆元。
- 求法
1.递推法:
i
n
v
[
i
]
=
−
(
p
/
i
)
∗
i
n
v
[
p
m
o
d
i
]
inv[i]=-(p/i)*inv[p mod i]
inv[i]=−(p/i)∗inv[pmodi](p是模数)
2.拓展欧几里得法:
先预处理一遍阶乘,求
i
i
i得逆元即对
i
i
i的阶乘做一遍拓展欧几里得;
- 应用:
1.逆元求组合数;
2.优雅地除以一个数(化除为乘);
- 代码
1.递推法:
#include<bits/stdc++.h>
using namespace std;
#define M 30000000
//map<long long,long long>inv;
int n,p;
long long inv[M+5];
void niyuan(int n,int p)
{
for(int i=2;i<=n;i++)
{
inv[i]=-p/i*inv[p%i];
while(inv[i]<0)
inv[i]+=p;
}
}
int main()
{
scanf("%d%d",&n,&p);
inv[1]=1;
niyuan(n,p);
for(int i=1;i<=n;i++)
printf("%I64d\n",inv[i]);
return 0;
}
2.拓展欧几里得法:
预处理阶乘:
a[0]=1
for(int i=1;i<=n+m;i++)
a[i]=a[i-1]*i%mod;//前缀积
求逆元:
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;y=0;
return;
}
ll xx,yy;
exgcd(b,a%b,xx,yy);
x=yy;
y=xx-(a/b)*yy;
}
ll inv(ll sum)
{
ll x,y;
exgcd(sum,mod,x,y);
x=(x%mod+mod)%mod;
return x;
}//求逆元,sum为a[i]
3.快速幂求逆元:
主函数内:
ans=inv(i,mod-2);
求逆元:
int inv(int x,int y)
{
int ans=1;
while(y)
{
if(y&1)ans=(ans*x)%mod;
y>>=1;
x=(x*x)%mod;
}
ans%=mod;
return ans;
}//快速幂求逆元
习题:
e
m
m
emm
emm好像逆元没有什么裸题吧,不过倒是有一道模板题:【模板】乘法逆元
还有一道神仙题(滑稽):【模板】乘法逆元2(其实这道题与逆元没有什么关系)
排列组合
- 排列
排列的分类:
1.选排列
最普通的排列,从
m
m
m个数选出
n
n
n个数的方案数。
A
m
n
=
(
m
−
n
)
!
A^n_m=(m-n)!
Amn=(m−n)!
2.错位排列(错排)
从
m
m
m个数选出
n
n
n个数,数
n
n
n不能在第
n
n
n个位置上的方案数。
f
(
n
)
=
(
n
−
1
)
∗
(
f
(
n
−
1
)
+
f
(
n
−
2
)
)
f(n)=(n-1)*(f(n-1)+f(n-2))
f(n)=(n−1)∗(f(n−1)+f(n−2))
3.圆排列
从
n
n
n个数选出
r
r
r个数围成一个圈的方案数。
A
n
r
/
r
A^r_n/r
Anr/r,若
r
=
n
r=n
r=n,则有(n-1)!种。
- 组合
C m n = m ! n ! ∗ ( m − n ) ! C^n_m=\frac{m!}{n!*(m-n)!} Cmn=n!∗(m−n)!m!
模板:逆元求组合数
#include<cstdio>
#define ll long long
using namespace std;
ll t,n,m,mod;
ll a[100005];
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;y=0;
return;
}
ll xx,yy;
exgcd(b,a%b,xx,yy);
x=yy;
y=xx-(a/b)*yy;
}
ll inv(ll sum)
{
ll x,y;
exgcd(sum,mod,x,y);
x=(x%mod+mod)%mod;
return x;
}//求逆元
ll C(ll x,ll y,ll mod)
{
if(x<y)
return 0;
return a[x]*inv(a[y])%mod*inv(a[x-y])%mod;
}//求组合数
int main()
{
a[0]=1;
scanf("%I64d",&t);
while(t--)
{
scanf("%I64d%I64d%I64d",&n,&m,&mod);
for(int i=1;i<=n+m;i++)
a[i]=a[i-1]*i%mod;//前缀积
printf("%I64d\n",C(n+m-1,m,mod));
}
return 0;
}
//方法:求C(n-1,m+n-1)%mod
应用:
1.夹棍法;
2.求杨辉三角;
3.二项式定理;
二项式定理
应用:杨辉三角
(
x
+
y
)
m
=
∑
i
=
0
i
≤
m
(
m
i
)
x
i
y
m
−
i
(x+y)^m=\sum^{i\leq m}_{i=0}(^i_m)x^iy^{m-i}
(x+y)m=∑i=0i≤m(mi)xiym−i
质数的判定和应用
- 质数的判定方法
1.暴力枚举法:
对于一个数
x
x
x,从2开始枚举到
x
\sqrt{x}
x(一个数最多有
x
\sqrt{x}
x个约数),若存在
i
i
i,使得
x
x
x%
i
i
i=0,则
x
x
x为合数,否则为质数。注意特判1和2.
若求1~
n
n
n中的所有质数,那么该算法的复杂度为
O
(
n
2
)
O(n^2)
O(n2)。
2.普通筛法:
假如求1~50的质数,一开始如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
划掉1,从2开始枚举,划掉除2以外2的质数:
| 2 | 3 | 5 | 7 | 9 | |||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 13 | 15 | 17 | 19 | |||||
| 21 | 23 | 25 | 27 | 29 | |||||
| 31 | 33 | 35 | 37 | 39 | |||||
| 41 | 43 | 45 | 47 | 49 |
接下来,划掉除3以外3的倍数:
| 2 | 3 | 5 | 7 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 13 | 17 | 19 | ||||||
| 23 | 25 | 29 | |||||||
| 31 | 35 | 37 | |||||||
| 41 | 43 | 47 | 49 |
划掉除5以外5的倍数:
| 2 | 3 | 5 | 7 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | ||||||||
| 41 | 43 | 47 | 49 |
划掉除7以外7的倍数:
| 2 | 3 | 5 | 7 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 13 | 17 | 19 | ||||||
| 23 | 29 | ||||||||
| 31 | 37 | ||||||||
| 41 | 43 | 47 |
到这里我们就筛完了。但细心地你会发现一个问题:一个数可能会被筛多次。举个例子,6在筛2的倍数时会被筛掉,在筛3的倍数时同样会被筛掉,这样就增加了此算法的事件复杂度。有没有办法使一个合数只会被筛一次呢?
3.线性筛:
定义两个数组:
m
a
r
k
[
i
]
mark[i]
mark[i]表示
i
i
i是否是质数,
p
r
i
m
e
[
i
]
prime[i]
prime[i]表示从小到大找到的质数。若
m
a
r
k
[
i
]
=
0
mark[i]=0
mark[i]=0,则吧
i
i
i加入进质数数组里。接下来,无论
i
i
i是否是质数,从1开始枚举
p
r
i
m
e
[
j
]
prime[j]
prime[j],将
m
a
r
k
[
i
∗
p
r
i
m
e
[
j
]
]
mark[i*prime[j]]
mark[i∗prime[j]]标记为合数,若
i
i
i%
p
r
i
m
e
[
j
]
prime[j]
prime[j]=0,说明
i
i
i是
p
r
i
m
e
[
j
]
prime[j]
prime[j]的倍数,跳出循环,保证每一个合数只会被筛一次。
举个例子,当
i
i
i为4时,质数数组有2和3,枚举质数2,标记42=8为合数。因为4是2的倍数,跳出循环。假如不跳出循环,那么下一个被枚举到的合数就是43=12,而12应该在枚举6*2时筛到,多筛了一遍,增加了时间复杂度。
4.Miller-Rabin素性测试:
玄学算法。
费马小定理:若
p
p
p是质数,则
∀
x
p
−
1
≡
1
(
m
o
d
p
)
\forall x^{p-1}\equiv1(mod p)
∀xp−1≡1(modp),但不是所有数只要满足
∀
x
p
−
1
≡
1
(
m
o
d
p
)
\forall x^{p-1}\equiv1(mod p)
∀xp−1≡1(modp)就是质数,所以光有这一个定理还不够;
二次探测定理:若
p
p
p是质数,且
∀
x
2
≡
1
(
m
o
d
p
)
\forall x^2\equiv1(mod p)
∀x2≡1(modp),则
(
x
+
1
)
(
x
−
1
)
≡
0
(
m
o
d
p
)
(x+1)(x-1)\equiv0(mod p)
(x+1)(x−1)≡0(modp),也就是说
x
≡
±
1
(
m
o
d
p
)
x\equiv\pm1(mod p)
x≡±1(modp)。
Miller-Rabin的流程:
设
p
p
p是大于2的奇数,另
p
−
1
=
d
∗
2
r
p-1=d*2^r
p−1=d∗2r,d为奇数;
随机选择一个
x
x
x,
首先判断费马小定理是否成立:
x
p
−
1
≡
=
1
(
m
o
d
p
)
x^{p-1}\equiv =1(mod p)
xp−1≡=1(modp);
若符合,则由二项式定理,要么
x
d
≡
1
(
m
o
d
p
)
x^d\equiv1(mod p)
xd≡1(modp),要么存在一个比
r
r
r小的数
i
i
i满足
x
d
∗
2
i
≡
−
1
(
m
o
d
p
)
x^{d*2^i}\equiv-1(mod p)
xd∗2i≡−1(modp)。
单次复杂度为
O
(
l
o
g
n
)
O(log n)
O(logn),多次随机
x
x
x可保证极高正确率。
- 代码
1.线性筛:
#include<bits/stdc++.h>
using namespace std;
int prime[10000005],mark[10000005],c[100005],tot,m,n;
void su()
{
int i,j;
for(i=2;i<=n;i++)
{
if(mark[i]==0)//是素数。
{
tot++;prime[tot]=i;
}//增加一个素数。
for(j=1;j<=tot;j++)
{
mark[i*prime[j]]=1;
if(i%prime[j]==0)
break;//标记倍数为合数,若遇到倍数,则停止。
}
}
}
int main()
{
int k;
scanf("%d%d",&n,&m);
su();
mark[1]=1;
for(k=1;k<=m;k++)
scanf("%d",&c[k]);
for(k=1;k<=m;k++)
if(mark[c[k]]==0)printf("Yes\n");
else printf("No\n");
return 0;
}
2.Miller-Rabin
#include<bits/stdc++.h>
using namespace std;
int prime[10000005],mark[10000005],c[100005],tot,m,n;
void su()
{
int i,j;
for(i=2;i<=n;i++)
{
if(mark[i]==0)//是素数。
{
tot++;prime[tot]=i;
}//增加一个素数。
for(j=1;j<=tot;j++)
{
mark[i*prime[j]]=1;
if(i%prime[j]==0)
break;//标记倍数为合数,若遇到倍数,则停止。
}
}
}
int main()
{
int k;
scanf("%d%d",&n,&m);
su();
mark[1]=1;
for(k=1;k<=m;k++)
scanf("%d",&c[k]);
for(k=1;k<=m;k++)
if(mark[c[k]]==0)printf("Yes\n");
else printf("No\n");
return 0;
}#include<bits/stdc++.h>
using namespace std;
int prime[10000005],mark[10000005],c[100005],tot,m,n;
void su()
{
int i,j;
for(i=2;i<=n;i++)
{
if(mark[i]==0)//是素数。
{
tot++;prime[tot]=i;
}//增加一个素数。
for(j=1;j<=tot;j++)
{
mark[i*prime[j]]=1;
if(i%prime[j]==0)
break;//标记倍数为合数,若遇到倍数,则停止。
}
}
}
int main()
{
int k;
scanf("%d%d",&n,&m);
su();
mark[1]=1;
for(k=1;k<=m;k++)
scanf("%d",&c[k]);
for(k=1;k<=m;k++)
if(mark[c[k]]==0)printf("Yes\n");
else printf("No\n");
return 0;
}
- 应用
大多数时候作为一种辅助算法,帮助解题(如Pollard-Rho)。
没什么裸题,都是很简单的那种。
但是线性筛素数还可以顺带预处理除一些积性函数,如欧拉函数,莫比乌斯函数等等。
一些题(双倍经验):
1.樱花
2.樱花
约数
- 唯一分解定理
就是分解质因数。 - 一些性质:
1.将
n
n
n分解质因数:
n
=
∏
p
i
r
i
n=\prod p_i^{r_i}
n=∏piri;
2.约数个数:
σ
0
(
n
)
=
∏
(
1
+
r
i
)
\sigma_0(n)=\prod (1+r_i)
σ0(n)=∏(1+ri);
3.约数和:
σ
1
(
n
)
=
∏
∑
k
=
0
r
i
p
i
\sigma_1(n)=\prod \sum^{r_i}_{k=0}p_i^{}
σ1(n)=∏∑k=0ripi;
4.约数函数:
σ
t
(
n
)
=
∑
d
∣
n
d
t
=
∏
∑
k
=
0
r
i
p
i
k
t
\sigma_t(n)=\sum_{d|n}dt=\prod \sum^{r_i}_{k=0}p_i^{kt}
σt(n)=∑d∣ndt=∏∑k=0ripikt;
以上这些东西,我也看不懂。
例题:
1.[AHOI2007]密码箱(数据过水);
2.[HAOI2007]反素数;
3.[JLOI2014]聪明的燕姿;
- 最大公因数(gcd)
最大公因数的性质:
1.
g
c
d
(
a
,
b
)
=
g
c
d
(
a
−
b
,
b
)
gcd(a,b)=gcd(a-b,b)
gcd(a,b)=gcd(a−b,b);
2.
g
c
d
(
a
,
b
)
=
g
c
d
(
a
%
b
,
b
)
gcd(a,b)=gcd(a\%b,b)
gcd(a,b)=gcd(a%b,b);
最大公因数的求法:
1.更相减损术;
2.欧几里得法。
代码:
#include<cstdio>
using namespace std;
int n,m;
int gcd(int x,int y)
{
return (y==0)?x:gcd(y,x%y);
}
int main()
{
scanf("%d%d",&n,&m);
printf("%d",gcd(n,m));
return 0;
}
例题:
1.NOIp2009 Hankson的趣味题
拓展欧几里得
-
应用
可求解同余方程 a x ≡ m ( m o d b ) ax\equiv m(mod b) ax≡m(modb),以及不定方程 a x + b y = g c d ( a , b ) ax+by=gcd(a,b) ax+by=gcd(a,b)。 -
方法
1.求解同余方程:
转化为
a
x
=
b
y
+
m
ax=by+m
ax=by+m,移项
a
x
−
b
y
=
m
ax-by=m
ax−by=m,另
y
=
−
y
y=-y
y=−y,转化为
a
x
+
b
y
=
m
ax+by=m
ax+by=m,但注意必须
g
c
d
(
a
,
b
)
∣
m
gcd(a,b)|m
gcd(a,b)∣m,否则无解。
2.求解不定方程:
对于
a
x
+
b
y
=
c
ax+by=c
ax+by=c,若满足
g
c
d
(
x
,
y
)
∣
c
gcd(x,y)|c
gcd(x,y)∣c,方程有解;反之则无解。
- 步骤
斐蜀定理:
a
x
+
b
y
=
g
c
d
(
a
,
b
)
ax+by=gcd(a,b)
ax+by=gcd(a,b)一定有解。
g
c
d
(
a
,
b
)
=
g
c
d
(
b
,
a
%
b
)
gcd(a,b)=gcd(b,a\%b)
gcd(a,b)=gcd(b,a%b)。
在欧几里得算法的最后一步时,有
b
=
0
b=0
b=0,
g
c
d
(
a
,
b
)
=
a
gcd(a,b)=a
gcd(a,b)=a,因为
1
∗
a
+
0
∗
0
=
a
1*a+0*0=a
1∗a+0∗0=a,所以此时
a
x
+
b
y
=
g
c
d
(
a
,
b
)
ax+by=gcd(a,b)
ax+by=gcd(a,b)有一组解
x
=
1
,
y
=
0
x=1,y=0
x=1,y=0。
当
b
!
=
0
b!=0
b!=0时,递归求解方程
b
x
+
(
a
%
b
)
y
=
g
c
d
(
b
,
a
%
b
)
bx+(a\%b)y=gcd(b,a\%b)
bx+(a%b)y=gcd(b,a%b),直到
b
=
0
b=0
b=0。
- 代码
#include<bits/stdc++.h>
using namespace std;
int a,b,x,y,s;
int gcd(int a,int b)
{
int r=a%b;
if(r==0)
return r;
a=b;b=r;
gcd(a,b);
}
void exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;
y=0;
return;
}
int c=a-(a/b)*b,xx,yy;
exgcd(b,c,xx,yy);
x=yy;y=xx-(a/b)*yy;
}
int main()
{
scanf("%d%d",&a,&b);
s=gcd(a,b);
exgcd(a,b,x,y);
printf("%d %d",x,y);
return 0;
}
-
应用:
求解一元二次方程或同于方程,有时也会用来求中国剩余定理和拓展中国剩余定理。 -
例题:
1.NOIP2012 同余方程;
2.青蛙的约会(怎么变蓝题了,我刚做的时候不是绿题吗
Q
A
Q
QAQ
QAQ)
大步小步算法(BSGS)
- 应用:求解高次同余方程
a x ≡ b ( m o d c ) a^x \equiv b(mod\ c) ax≡b(mod c)
其中 g c d ( a , c ) = 1 gcd(a,c)=1 gcd(a,c)=1。 - 由于我也证不来为什么算法是对的,所以我直接粘贴代码了
q
w
q
qwq
qwq:
看这篇大佬的博客吧:BSGS及扩展BSGS
#include<cstdio>
#include<cmath>
#include<map>
#define ll long long
using namespace std;
ll a,b,p,ans;
map<ll,ll>mp;
map<ll,bool>vis;
ll quick(ll x,ll y)
{
ll ret=1;
while(y)
{
if(y&1)ret=(ret*x)%p;
x=(x*x)%p;
y>>=1;
}
return ret;
}
ll bsgs(ll a,ll b)
{
mp.clear();vis.clear();
ll q=sqrt(p);
b%=p;
for(ll i=0;i<=q;++i)
{
ll ret=b*quick(a,i)%p;
mp[ret]=i;
vis[ret]=true;
}
a=quick(a,q);
if(a==0)return b==0?1:-1;
for(ll i=0;i<=q;++i)
{
ll ret=quick(a,i);
if(vis[ret])
{
ll j=mp[ret];
if(j>=0&&i*q-j>=0)
return i*q-j;
}
}
return -1;
}
int main()
{
while(scanf("%lld%lld%lld",&p,&a,&b)!=EOF)
{
ans=bsgs(a,b);
if(ans==-1)printf("no solution\n");
else printf("%lld\n",ans);
}
return 0;
}
- 例题:
1.UVA10225 Discrete Logging(模板题);
2.【SDOI2013】随机数生成器;
a i − 1 ≡ x i + b a + 1 x 1 + a − 1 a^{i-1} \equiv \frac{x_i+\frac{b}{a+1}}{x_1+\frac{}{a-1}} ai−1≡x1+a−1xi+a+1b
其中 x i = t x_i=t xi=t;
3.【SDOI2011】计算器;
拓展大步小步算法
与普通的bsgs类似,但可以处理模数不为质数的情况。直接贴代码了:
#include<cstdio>
#include<cmath>
#include<map>
#define ll long long
using namespace std;
ll a,b,p,ans;
map<ll,ll>mp;
map<ll,bool>vis;
ll gcd(ll x,ll y)
{
return (y==0)?x:gcd(y,x%y);
}
ll quick(ll x,ll y,ll mod)
{
ll ret=1;
while(y)
{
if(y&1)ret=ret*x%mod;
x=x*x%mod;
y>>=1;
}
return ret;
}
ll exbsgs(ll a,ll b,ll mod)
{
if(b==1)return 0;
ll k=0,tmp=1,d;
while(1)
{
d=gcd(a,mod);
if(d==1)break;
if(b%d)return -1;
b/=d;mod/=d;
tmp=tmp*(a/d)%mod;
k++;
if(tmp==b)return k;
}
mp.clear();
vis.clear();
ll mul=b,q=ceil(sqrt(mod));
mp[b]=0;
for(int i=1;i<=q;++i)
{
mul=mul*a%mod;
mp[mul]=i;
vis[mul]=true;
}
ll qq=quick(a,q,mod);
mul=tmp;
for(int i=1;i<=q;++i)
{
mul=mul*qq%mod;
if(vis[mul])return i*q-mp[mul]+k;
}
return -1;
}
int main()
{
while(scanf("%lld%lld%lld",&p,&a,&b)!=EOF)
{
ans=exbsgs(a,b,p);
if(ans==-1)printf("no solution\n");
else printf("%lld\n",ans);
}
return 0;
}
快速乘和快速幂
- 应用:快速地做乘法或幂运算,多为辅助算法。
- 代码:
1.快速乘(乘法变加法)
#include<bits/stdc++.h>
using namespace std;
long long a,b,s,sum;
long long fast(long long a,long long b,long long mod)
{
long long ans=0;
while(b)
{
if(b%2)
{
ans+=a;
ans%=mod;
}
a+=a;
a%=mod;
b/=2;
}
return ans;
}
int main()
{
scanf("%I64d%I64d%I64d",&a,&b,&s);
sum=fast(a,b,s);
printf("%I64d",sum);
return 0;
}
2.快速幂:
#include<bits/stdc++.h>
using namespace std;
int a,b,s,sum;
int fast(int a,int b,int mod)
{
int ans=1;
while(b)
{
if(b%2)
{
ans*=a;
ans%=mod;
}
a*=a;
a%=mod;
b=b>>1;
}
return ans;
}
int main()
{
scanf("%d%d%d",&a,&b,&s);
sum=fast(a,b,s);
printf("%d",sum);
return 0;
}
矩阵相关
- 矩阵
这个就叫矩阵:
[ a 11 , a 12 , . . . , a 1 n a 21 , a 22 , . . . , a 2 n . . . , . . . , . . . , . . . a n 1 , a n 2 , . . . , a n n ] \left[\begin{aligned} a_{11},a_{12},...,a_{1n}\\ a_{21},a_{22},...,a_{2n}\\ ...,...,...,...\\ a_{n1},a_{n2},...,a_{nn} \end{aligned}\right] ⎣⎢⎢⎢⎢⎡a11,a12,...,a1na21,a22,...,a2n...,...,...,...an1,an2,...,ann⎦⎥⎥⎥⎥⎤ - 矩阵运算
1.矩阵加减:
条件:两个矩阵长宽一样,例如
[
1
4
2
2
0
0
]
+
[
0
0
5
7
5
0
]
=
[
1
+
0
4
+
0
2
+
5
2
+
7
0
+
5
0
+
0
]
=
[
1
4
7
9
5
0
]
\left[\begin{aligned}1\ 4\ 2\\2\ 0\ 0\end{aligned}\right]+\left[\begin{aligned}0\ 0\ 5\\7\ 5\ 0\end{aligned}\right]=\left[\begin{aligned}1+0\ 4+0\ 2+5\\2+7\ 0+5\ 0+0\end{aligned}\right]=\left[\begin{aligned}1\ 4\ 7\\9\ 5\ 0\end{aligned}\right]
[1 4 22 0 0]+[0 0 57 5 0]=[1+0 4+0 2+52+7 0+5 0+0]=[1 4 79 5 0]
减法类似;
2.矩阵乘法:
条件:第一个矩阵的行数和第二个矩阵的列数相等。
[
1
0
2
−
1
3
1
]
∗
[
3
1
2
1
1
0
]
=
[
(
1
∗
3
+
0
∗
2
+
2
∗
1
)
(
1
∗
1
+
0
∗
1
+
2
∗
0
)
(
−
1
∗
3
+
3
∗
2
+
1
∗
1
)
(
−
1
∗
1
+
3
∗
1
+
1
∗
0
)
]
=
[
5
1
4
2
]
\left[\begin{aligned}1\ 0\ 2\\-1\ 3\ 1\end{aligned}\right]*\left[\begin{aligned}3\ 1\\ 2\ 1\\1\ 0\end{aligned}\right]=\left[\begin{aligned}(1*3+0*2+2*1)\ (1*1+0*1+2*0)\\ (-1*3+3*2+1*1)\ (-1*1+3*1+1*0)\end{aligned}\right]=\left[\begin{aligned}5\ 1\\ 4\ 2\end{aligned}\right]
[1 0 2−1 3 1]∗⎣⎢⎡3 12 11 0⎦⎥⎤=[(1∗3+0∗2+2∗1) (1∗1+0∗1+2∗0)(−1∗3+3∗2+1∗1) (−1∗1+3∗1+1∗0)]=[5 14 2]
3.矩阵的幂:
[
a
11
,
a
12
,
.
.
.
,
a
1
n
a
21
,
a
22
,
.
.
.
,
a
2
n
.
.
.
,
.
.
.
,
.
.
.
,
.
.
.
a
n
1
,
a
n
2
,
.
.
.
,
a
n
n
]
2
=
[
a
11
,
a
12
,
.
.
.
,
a
1
n
a
21
,
a
22
,
.
.
.
,
a
2
n
.
.
.
,
.
.
.
,
.
.
.
,
.
.
.
a
n
1
,
a
n
2
,
.
.
.
,
a
n
n
]
∗
[
a
11
,
a
12
,
.
.
.
,
a
1
n
a
21
,
a
22
,
.
.
.
,
a
2
n
.
.
.
,
.
.
.
,
.
.
.
,
.
.
.
a
n
1
,
a
n
2
,
.
.
.
,
a
n
n
]
\left[\begin{aligned} a_{11},a_{12},...,a_{1n}\\ a_{21},a_{22},...,a_{2n}\\ ...,...,...,...\\ a_{n1},a_{n2},...,a_{nn} \end{aligned}\right]^2=\left[\begin{aligned} a_{11},a_{12},...,a_{1n}\\ a_{21},a_{22},...,a_{2n}\\ ...,...,...,...\\ a_{n1},a_{n2},...,a_{nn} \end{aligned}\right]*\left[\begin{aligned} a_{11},a_{12},...,a_{1n}\\ a_{21},a_{22},...,a_{2n}\\ ...,...,...,...\\ a_{n1},a_{n2},...,a_{nn} \end{aligned}\right]
⎣⎢⎢⎢⎢⎡a11,a12,...,a1na21,a22,...,a2n...,...,...,...an1,an2,...,ann⎦⎥⎥⎥⎥⎤2=⎣⎢⎢⎢⎢⎡a11,a12,...,a1na21,a22,...,a2n...,...,...,...an1,an2,...,ann⎦⎥⎥⎥⎥⎤∗⎣⎢⎢⎢⎢⎡a11,a12,...,a1na21,a22,...,a2n...,...,...,...an1,an2,...,ann⎦⎥⎥⎥⎥⎤
- 矩阵快速幂
是一种求矩阵的幂的方法,快速幂套矩阵乘法即可
#include<cstdio>
#include<iostream>
#define mod 1000000007
#define ll long long
using namespace std;
struct node
{
ll m[105][105];
}a,e;//a是输入的矩阵,ans是答案矩阵,e是单位矩阵
ll n,k;
node mul(node x,node y)
{
node nw;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
nw.m[i][j]=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
{
nw.m[i][j]=nw.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod;
}
return nw;
}//矩阵乘法
node quickk(node x,ll y)
{
node pre=e;
while(y)
{
if(y&1)
pre=mul(pre,x);
x=mul(x,x);
y>>=1;
}
return pre;
}//快速幂主体
int main()
{
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%lld",&a.m[i][j]);
for(int i=1;i<=n;i++)
e.m[i][i]=1;//构造单位矩阵
node ans=quickk(a,k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
printf("%lld ",ans.m[i][j]%mod);
printf("\n");
}
return 0;
}
- 矩阵加速
难点:构造矩阵
若把运算放在矩阵中,会大大提高运算效率。
举个例子:
a [ 1 ] = a [ 2 ] = a [ 3 ] = 1 a[1]=a[2]=a[3]=1 a[1]=a[2]=a[3]=1
a [ x ] = a [ x − 3 ] + a [ x − 1 ] ( x > 3 ) a[x]=a[x-3]+a[x-1] (x>3) a[x]=a[x−3]+a[x−1](x>3)
求 a a a数列的第 n n n项对1000000007 ( 1 0 9 + 7 ) (10^9+7) (109+7)取余的值。
n n n很大,如果递推求会超时。
但是如果我们把这个模型放在矩阵中,求第二项就会变成求这个东西:
[ 1 0 0 0 1 0 1 0 1 ] 2 \left[\begin{aligned}1\ 0\ 0\\0\ 1\ 0\\1\ 0\ 1 \end{aligned}\right]^2 ⎣⎢⎡1 0 00 1 01 0 1⎦⎥⎤2
求第 n n n项:
[ 1 0 0 0 1 0 1 0 1 ] n \left[\begin{aligned}1\ 0\ 0\\0\ 1\ 0\\1\ 0\ 1 \end{aligned}\right]^n ⎣⎢⎡1 0 00 1 01 0 1⎦⎥⎤n
输出 ( 1 , 1 ) (1,1) (1,1)。
代码:
#include<cstdio>
#define ll long long
#define mod 1000000007
using namespace std;
struct node
{
ll m[4][13];
}stp,e,ans;
ll n;
int t;
node mul(node x,node y)
{
node nw;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
nw.m[i][j]=0;
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
for(int k=1;k<=3;k++)
{
nw.m[i][j]=(nw.m[i][j]%mod+x.m[i][k]*y.m[k][j]%mod)%mod;
}
return nw;
}//矩阵乘法
node quickk(node x,ll y)
{
node pre=e;
while(y)
{
if(y&1)
pre=mul(pre,x);
x=mul(x,x);
y>>=1;
}
return pre;
}//快速幂主体
int main()
{
stp.m[1][14]=1;
stp.m[1][15]=1;
stp.m[2][16]=1;
stp.m[3][17]=1;
for(int i=1;i<=3;i++)
e.m[i][i]=1;
scanf("%d",&t);
while(t--)
{
for(int i=1;i<=3;i++)
for(int j=1;j<=3;j++)
ans.m[i][j]=0;
scanf("%lld",&n);
ans=quickk(stp,n-1);
printf("%lld\n",ans.m[1][18]);
}
return 0;
}
例题:
1.【模板】矩阵加速(数列)
2.斐波那契数列
欧拉函数
- 概念:1~ x x x-1中与 x x x互质的数的个数。
- 特点:欧拉函数是积性函数。
- 代码:
1.线性求欧拉函数(求素数时顺便求):
#include<cstdio>
#define maxn 1000005
using namespace std;
int n;
int phi[maxn],prime[maxn],tot,ans;
bool mark[maxn];
void getphi()
{
phi[1]=1;
for(int i=2;i<=n;++i)
{
if(!mark[i])
{
prime[++tot]=i;
phi[i]=i-1;
}//质数的phi
for(int j=1;j<=tot;++j)
{
if(i*prime[j]>n)break;
mark[i*prime[j]]=1;//标记合数
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
int main()
{
scanf("%d",&n);
getphi();
for(int i=1;i<=n;++i)
printf("%d ",phi[i]);
return 0;
}
2.非线性:
#include<bits/stdc++.h>
using namespace std;
int phi(int x)
{
int ans=x;
for(int i=2;i*i<=x;i++)
{
if(x%i==0)
{
ans=ans/i*(i-1);
while(x%i==0)x/=i;
}
}
if(x>1)ans=ans/x*(x-1);//x为质数
return ans;
}
int main()
{
int n;
while(scanf("%d",&n)==1)
printf("%d\n",phi(n));
return 0;
}
欧拉定理及费马小定理
- 欧拉定理:若 a a a与 m m m互质,则 a φ ( m ) ≡ 1 ( m o d m ) a^{\varphi(m)}\equiv 1(mod\ m) aφ(m)≡1(mod m);
- 拓展欧拉定理:若 r > φ ( m ) r>\varphi(m) r>φ(m),则 a r ≡ a r m o d φ ( m ) + φ ( m ) ( m o d m ) a^r\equiv a^{r\ mod\ \varphi(m)+\varphi(m)}(mod\ m) ar≡ar mod φ(m)+φ(m)(mod m);
- 费马小定理: a p − 1 ≡ 1 ( m o d q ) a^{p-1}\equiv 1(mod\ q) ap−1≡1(mod q),其中 q q q为质数。(费马小定理是欧拉定理的特殊形式)
- 代码
欧拉定理:
#include<cstdio>
#define ll long long
using namespace std;
ll a,b,m;
ll tmp,phi,flag;
char ch;
ll quick(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1)ans=ans*x%m;
x=x*x%m;
y>>=1;
}
return ans;
}
int main()
{
scanf("%lld%lld",&a,&m);
tmp=phi=m;
for(ll i=2;i*i<=m;++i)
{
if(tmp%i)continue;
phi-=phi/i;
while(tmp%i==0)
tmp/=i;
}
if(tmp>1)
phi-=phi/tmp;
while((ch=getchar())<'0'||ch>'9');
b=ch-'0';
if(b>=phi)
{
flag=1;
b%=phi;
}
while((ch=getchar())>='0'&&ch<='9')
{
b=b*10+ch-'0';
if(b>=phi)
{
flag=1;
b%=phi;
}
}
if(flag)b+=phi;
printf("%lld",quick(a,b));
return 0;
}
模板题:【模板】欧拉定理
中国剩余定理
- 作用:用于求解同余方程组:
{ x ≡ b 1 ( m o d m 1 ) x ≡ b 2 ( m o d m 2 ) . . . . . . . . . . . . . . . . x ≡ b n ( m o d m n ) \left\{\begin{aligned}x\equiv b_1(mod\ m_1)\\x\equiv b_2(mod\ m_2)\\................\\x\equiv b_n(mod\ m_n)\end{aligned}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x≡b1(mod m1)x≡b2(mod m2)................x≡bn(mod mn)
其中 m 1 , m 2 , . . . , m n m_1,m_2,...,m_n m1,m2,...,mn互质。 - 代码
#include<cstdio>
#define maxn 100005
using namespace std;
int n;
int a[maxn],m[maxn];
void exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;
y=0;
return;
}
int c=a-(a/b)*b,xx,yy;
exgcd(b,c,xx,yy);
x=yy;y=xx-(a/b)*yy;
}
int china(int w[],int b[],int k)
{
int x,y,a=0,m,n=1;
for(int i=1;i<=k;++i)
n*=w[i];
for(int i=1;i<=k;++i)
{
m=n/w[i];
exgcd(w[i],m,x,y);
a=(a+y*m*b[i])%n;
}
if(a>0)return a;
else return a+n;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d%d",&m[i],&a[i]);
printf("%d",china(m,a,n));
return 0;
}
拓展中国剩余定理
- 作用
用于解同余方程组,但模数两两之间可以不互质。 - 证明
我写的博客:拓展中国剩余定理 - 代码
#include<cstdio>
#define ll long long
using namespace std;
ll n,a,b,tot,M;
ll ans,x,y,r;
ll flag=1,mul;
ll exgcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;y=0;
return a;
}
ll d=exgcd(b,a%b,x,y);
ll t=y;
y=x-(a/b)*y;
x=t;
return d;
}//求解同余方程
ll quick_mul(ll nw,ll aim,ll mod)
{
ll res=0;
while(aim>0)
{
if(aim&1)res=(res+nw)%mod;
nw=(nw+nw)%mod;
aim>>=1;
}
return res;
}//龟速乘QAQ(模板)
int main()
{
scanf("%I64d",&n);
while(n--)
{
x=0;
y=0;
tot++;//tot计数
scanf("%I64d%I64d",&a,&b);
if(tot==1)
{
ans=b;
M=a;
continue;
}//初始化
r=exgcd(M,a,x,y);//求最大公因数
mul=((b-ans)%a+a)%a;
x=quick_mul(x,mul/r,a);
if((b-ans)%r!=0)
{
flag=0;
continue;
}//判断无解
ans=ans+(x*M);
M=(M*a)/r;//更新最小公倍数
ans=(ans%M+M)%M;//保证ans为正值
}
if(flag)
printf("%I64d",ans);
else
printf("No");
return 0;
}
卢卡斯定理
- 作用
求 C n m % p C^m_n\%p Cnm%p( p p p为质数)的值。 - 定理:
1. C n m = C n / p m / p ∗ C n % p m % p C^m_n=C^{m/p}_{n/p}*C^{m\%p}_{n\%p} Cnm=Cn/pm/p∗Cn%pm%p
2.将 n , m n,m n,m写成 p p p进制:
C n m = C n k − 1 m k − 1 ∗ C n k − 2 m k − 2 ∗ . . . ∗ C n 0 m 0 ( m o d p ) C^m_n=C^{m_{k-1}}_{n_{k-1}}*C^{m_{k-2}}_{n_{k-2}}*...*C^{m_0}_{n_0}(mod\ p) Cnm=Cnk−1mk−1∗Cnk−2mk−2∗...∗Cn0m0(mod p) - 代码:
#include<cstdio>
#define ll long long
using namespace std;
ll t,n,m,p;
ll quick(ll x,ll y)
{
ll ret=1;
while(y)
{
if(y&1)ret=(ret*x)%p;
x=(x*x)%p;
y>>=1;
}
return ret;
}
ll C(ll n,ll m)
{
if(n<m)return 0;
if(m>n-m)m=n-m;
ll s1=1,s2=1;
for(ll i=0;i<m;++i)
{
s1=s1*(n-i)%p;
s2=s2*(i+1)%p;
}
return s1*quick(s2,p-2)%p;
}
ll lucas(ll n,ll m)
{
if(m==0)return 1;
return C(n%p,m%p)*lucas(n/p,m/p)%p;
}
int main()
{
scanf("%lld",&t);
while(t--)
{
scanf("%lld%lld%lld",&n,&m,&p);
printf("%lld\n",lucas(m+n,m));
}
return 0;
}
模板题:【模板】卢卡斯定理
拓展卢卡斯定理
- 作用:同卢卡斯定理,只是 p p p不一定为质数。但其实与卢卡斯定理没什么关系。
- 代码(我证不来 Q A Q QAQ QAQ):
#include<cstdio>
#include<cmath>
#define ll long long
#define maxn 1000005
using namespace std;
ll n,m,p;
ll A[maxn],B[maxn];
ll gcd(ll a,ll b)
{
return (b==0)?a:gcd(b,a%b);
}
void exgcd(ll a,ll b,ll &x,ll &y)
{
if(b==0)
{
x=1;
y=0;
return;
}
ll c=a-(a/b)*b,xx,yy;
exgcd(b,c,xx,yy);
x=yy;y=xx-(a/b)*yy;
}
ll inv(ll a,ll b)
{
ll x,y;
exgcd(a,b,x,y);
return (x+b)%b;
}
ll quick(ll x,ll y,ll mod)
{
ll ret=1;
while(y)
{
if(y&1)ret=(ret*x)%mod;
x=(x*x)%mod;
y>>=1;
}
return ret;
}
ll f(ll n,ll x,ll y)
{
if(n==0)return 1;
ll ret=1;
for(ll i=2;i<=y;++i)
{
if(i%x)
ret=(ret*i)%y;
}
ret=quick(ret,n/y,y);
for(ll i=2;i<=n%y;++i)
{
if(i%x)
ret=(ret*i)%y;
}
return ret*f(n/x,x,y)%y;
}
ll china(ll x,ll y)
{
return x*inv(p/y,y)%p*(p/y)%p;
}
ll C(ll n,ll m,ll x,ll y)
{
ll f1=f(n,x,y),f2=f(m,x,y),f3=f(n-m,x,y);
ll ret=0;
for(ll i=n;i;i/=x)ret+=i/x;
for(ll i=m;i;i/=x)ret-=i/x;
for(ll i=n-m;i;i/=x)ret-=i/x;
return f1*inv(f2,y)%y*inv(f3,y)%y*quick(x,ret,y)%y;
}
ll exlucas(ll n,ll m,ll mod)
{
ll ret=0,q=sqrt(mod)+5,x,tmp=mod;
for(ll i=2;i<=q;++i)
{
if(tmp%i)continue;
x=1;
while(tmp%i==0)
{
x*=i;
tmp/=i;
}
ret=(ret+china(C(n,m,i,x),x))%mod;
}
if(tmp>1)ret=(ret+china(C(n,m,tmp,tmp),tmp))%mod;
return ret;
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&p);
printf("%lld",exlucas(n,m,p));
return 0;
}
狄利克雷卷积
-
概念
定义一种运算:
h = f ⨂ g h=f\bigotimes g h=f⨂g
为:
h ( n ) = ∑ d ∣ n f ( d ) g ( d n ) h(n)=\sum_{d|n}f(d)g(\frac{d}{n}) h(n)=d∣n∑f(d)g(nd)
这就是狄利克雷卷积的一种表现形式(详情见博客:Greninja_Wu 狄利克雷卷积)。
若 f f f, g g g为积性函数,则 h h h也为积性函数。 -
应用
莫比乌斯反演。
本章完。
莫比乌斯函数
- 概念
定义:
μ ( n ) = { 0 , p 2 ∣ n ( − 1 ) r , n = p 1 ∗ p 2 ∗ . . . ∗ p r \mu(n)=\left\{\begin{aligned}0,p^2|n\\(-1)^r,n=p_1*p_2*...*p_r\end{aligned}\right. μ(n)={0,p2∣n(−1)r,n=p1∗p2∗...∗pr - 作用
常用于与约数相关的容斥。 - 求法
可以线性筛预处理(同欧拉函数)。 - 代码
#include<cstdio>
#define maxn 1000005
using namespace std;
int n;
int mu[maxn],prime[maxn],tot,ans;
bool mark[maxn];
void getmu()
{
mu[1]=1;
for(int i=2;i<=n;++i)
{
if(!mark[i])
{
prime[++tot]=i;
mu[i]=-1;
}//质数的phi
for(int j=1;j<=tot;++j)
{
if(i*prime[j]>n)break;
mark[i*prime[j]]=1;//标记合数
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else mu[i*prime[j]]=-mu[i];
}
}
}
int main()
{
scanf("%d",&n);
getmu();
for(int i=1;i<=n;++i)
printf("%d ",mu[i]);
return 0;
}
莫比乌斯反演
- 前置定理:
1. ∑ d ∣ n μ ( d ) = [ n = 1 ] \sum_{d|n}\mu(d)=[n=1] d∣n∑μ(d)=[n=1]
也就是说,当 n = 1 n=1 n=1时,上式的值为1,否则为0.
2. ∑ d ∣ n φ ( d ) = n \sum_{d|n}\varphi(d)=n d∣n∑φ(d)=n - 结论
给定数论函数 f f f和 g g g:
若 f f f满足 f ( n ) = ∑ d ∣ n g ( d ) f(n)=\sum_{d|n}g(d) f(n)=∑d∣ng(d),则 g g g满足$ g(n)=\sum_{d|n}\mu(d)*f(\frac{n}{d})$ - 证明
∑ d ∣ n μ ( d ) ∗ f ( n d ) = ∑ d ∣ n μ ( d ) ∑ d ′ ∣ n d g ( d ′ ) = ∑ d ′ ∣ n g ( d ′ ) ∑ d ∣ n d ′ μ ( d ) = g ( n ) \sum_{d|n}\mu(d)*f(\frac{n}{d})=\sum_{d|n}\mu(d)\sum_{d^{'}|\frac{n}{d}}g(d^{'})=\sum_{d^{'}|n}g(d^{'})\sum_{d|\frac{n}{d^{'}}}\mu(d)=g(n) ∑d∣nμ(d)∗f(dn)=∑d∣nμ(d)∑d′∣dng(d′)=∑d′∣ng(d′)∑d∣d′nμ(d)=g(n) - 应用
将很复杂的式子变形成为很简单的式子。 - 例题
1.【SDOI2015】约数个数和;
2.【POI2007】ZAP-Queries;
双倍经验:
3.GCD;
4.YY的GCD; - 总结
这种题通常是先把复杂的式子化为简单的式子,再用数论分块来做。
这里以ZAP为例:
目标公式: ∑ i = 1 m ∑ j = 1 n [ g c d ( i , j ) = k ] \sum^m_{i=1}\sum^n_{j=1}[gcd(i,j)=k] i=1∑mj=1∑n[gcd(i,j)=k]
转化:
∑ i = 1 m ∑ j = 1 n [ g c d ( i , j ) = k ] \sum^m_{i=1}\sum^n_{j=1}[gcd(i,j)=k] ∑i=1m∑j=1n[gcd(i,j)=k]
= ∑ i = 1 m ∑ j = 1 n ∑ d ∣ g c d ( i , k ) / k μ ( d ) =\sum^m_{i=1}\sum^n_{j=1}\sum_{d|gcd(i,k)/k}\mu(d) =∑i=1m∑j=1n∑d∣gcd(i,k)/kμ(d)
= ∑ d μ ( d ) ∑ k d ∣ i m ∑ k d ∣ j n 1 =\sum_d\mu(d)\sum^m_{kd|i}\sum^n_{kd|j}1 =∑dμ(d)∑kd∣im∑kd∣jn1
= ∑ d μ ( d ) ⌊ m k d ⌋ ⌊ n k d ⌋ =\sum_d\mu(d)\lfloor \frac{m}{kd} \rfloor \lfloor \frac{n}{kd} \rfloor =∑dμ(d)⌊kdm⌋⌊kdn⌋;
预处理 ⌊ m k d ⌋ \lfloor \frac{m}{kd} \rfloor ⌊kdm⌋和 ⌊ n k d ⌋ \lfloor \frac{n}{kd} \rfloor ⌊kdn⌋ - 代码:
#include<cstdio>
#include<algorithm>
#define ll long long
#define maxn 50005
using namespace std;
ll t,a,b,d,tot;
ll prime[maxn],mu[maxn],sum[maxn];
bool mark[maxn];
void getmu()
{
mu[1]=1;
for(ll i=2;i<=50000;++i)
{
if(!mark[i])
{
prime[++tot]=i;
mu[i]=-1;
}
for(ll j=1;j<=tot;++j)
{
if(i*prime[j]>50000)break;
mark[i*prime[j]]=1;
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else mu[i*prime[j]]=-mu[i];
}
}
for(ll i=1;i<=50000;++i)
sum[i]=sum[i-1]+mu[i];
}
int main()
{
getmu();
scanf("%lld",&t);
while(t--)
{
ll n,ans=0;
scanf("%lld%lld%lld",&a,&b,&d);
n=min(a,b);
for(ll l=1,r;l<=n;l=r+1)
{
r=min(a/(a/l),b/(b/l));
ans+=(a/(l*d))*(b/(l*d))*(sum[r]-sum[l-1]);
}
printf("%lld\n",ans);
}
return 0;
}
杜教筛
- 应用
求前缀和。
其实求前缀和可以用线性的方法,但是当 n n n很大(如 1 0 10 10^{10} 1010)时,就必须使用杜教筛了。 - 实质
记忆化搜索。 - 实现方法
定义数论函数 f f f, g g g, h h h,其中 h = f ⨂ g h=f\bigotimes g h=f⨂g。
目标是求 f f f的前缀和 S ( n ) = ∑ i = 1 n f ( i ) S(n)=\sum^n_{i=1}f(i) S(n)=∑i=1nf(i),而 h h h的前缀和易求,可用此方法。 - 关键:找 g g g和 h h h
- 过程
∑ i = 1 n h ( i ) \sum^n_{i=1}h(i) ∑i=1nh(i)
= ∑ i = 1 n ∑ j ∣ i f ( j ) g ( i j ) =\sum^n_{i=1}\sum_{j|i}f(j)g(\frac{i}{j}) =∑i=1n∑j∣if(j)g(ji)(狄利克雷卷积)
= ∑ i = 1 n g ( i ) ∑ j = 1 ⌊ n / i ⌋ f ( j ) =\sum^n_{i=1}g(i)\sum^{\lfloor n/i \rfloor}_{j=1}f(j) =∑i=1ng(i)∑j=1⌊n/i⌋f(j)(玄学变换)
= ∑ i = 1 n g ( i ) S ( ⌊ n i ⌋ ) =\sum^n_{i=1}g(i)S(\lfloor \frac{n}{i} \rfloor) =∑i=1ng(i)S(⌊in⌋)
= g ( 1 ) S ( n ) + ∑ i = 2 n g ( i ) S ( ⌊ n i ⌋ ) =g(1)S(n)+\sum^n_{i=2}g(i)S(\lfloor \frac{n}{i} \rfloor) =g(1)S(n)+∑i=2ng(i)S(⌊in⌋)
即:
S
(
n
)
=
∑
i
=
1
n
h
(
i
)
−
∑
i
=
2
n
g
(
i
)
S
(
⌊
n
i
⌋
)
g
(
1
)
S(n)=\frac{\sum^n_{i=1}h(i)-\sum^n_{i=2}g(i)S(\lfloor \frac{n}{i} \rfloor)}{g(1)}
S(n)=g(1)∑i=1nh(i)−∑i=2ng(i)S(⌊in⌋)
用数论分块即可求出正解。
总复杂度:
O
(
n
3
4
)
O(n^{\frac{3}{4}})
O(n43)
- 模板
先预处理出小范围的答案,大范围的用map存。
求 ∑ i = 1 n μ ( i ) \sum^n_{i=1} \mu(i) ∑i=1nμ(i)
#include<cstdio>
#include<algorithm>
#include<map>
#define ll long long
#define maxn 5000005
#define mod 1000000007
using namespace std;
map<ll,ll>mp;
ll n,m,tot;
ll ans[maxn],mu[maxn],prime[maxn];
bool mark[maxn];
void getmu()
{
mu[1]=1;
for(ll i=2;i<=m;++i)
{
if(!mark[i])
{
prime[++tot]=i;
mu[i]=-1;
}//质数的phi
for(ll j=1;j<=tot;++j)
{
if(i*prime[j]>m)break;
mark[i*prime[j]]=1;//标记合数
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
else mu[i*prime[j]]=-mu[i];
}
}
}
inline ll f(ll n)
{
if(n<=5000000)return ans[n];
if(mp.find(n)!=mp.end())return mp[n];
ll ret=1;
for(ll l=2,r;l<=n;l=r+1)
{
r=n/(n/l);
ret-=(r-l+1)*f(n/l);
ret=(ret%mod+mod)%mod;
}
return mp[n]=ret%mod;
}
int main()
{
scanf("%lld",&n);
m=min(n,(ll)5000000);
getmu();
for(ll i=1;i<=m;++i)
{
ans[i]=(ans[i-1]+i*mu[i])%mod;
ans[i]=(ans[i]+mod)%mod;
}
printf("%lld",f(n));
return 0;
}
- 例题
【模板】杜教筛(卡常好题)。
快速傅里叶变换(FFT)
-
复数
1.形如: a + b i a+bi a+bi的数,其中 i 2 = − 1 i^2=-1 i2=−1。
2.四则运算:
a. ( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i (a+bi)+(c+di)=(a+c)+(b+d)i (a+bi)+(c+di)=(a+c)+(b+d)i;
b. ( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i (a+bi)-(c+di)=(a-c)+(b-d)i (a+bi)−(c+di)=(a−c)+(b−d)i;
c. ( a + b i ) ∗ ( c + d i ) = ( a c − b d ) + ( b c + a d ) i (a+bi)*(c+di)=(ac-bd)+(bc+ad)i (a+bi)∗(c+di)=(ac−bd)+(bc+ad)i;
d.除法被吞了 q w q qwq qwq; -
单位复数根:
1.欧拉公式: e i x = cos x + i sin x e^{ix}=\cos x+i\sin x eix=cosx+isinx;
2.设 ω n k \omega^k_n ωnk表示 n n n的 k k k次复根,即把一个平面均分成 n n n份,取逆时针前 k k k份。当 n = 8 n=8 n=8时, ω n k \omega^k_n ωnk如下:
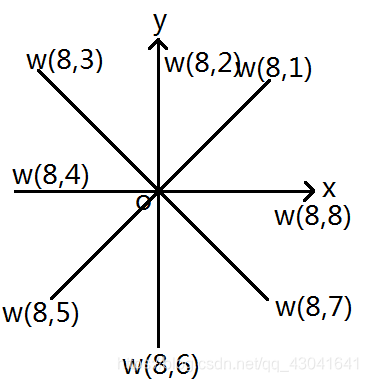
3.根据欧拉公式: ω n k = cos ( 2 π k n ) + i sin ( 2 π k n ) \omega^k_n=\cos (\frac{2\pi k}{n})+i\sin (\frac{2\pi k}{n}) ωnk=cos(n2πk)+isin(n2πk)
4.性质:
a. ω n n = ω n 0 = 1 \omega^n_n=\omega^0_n=1 ωnn=ωn0=1;
b.消去引理: ω d n d k = ω n k \omega^{dk}_{dn}=\omega^{k}_{n} ωdndk=ωnk;
c.折半引理: ( ω n k ) 2 = ω n 2 k (\omega^k_n)^2=\omega^k_{\frac{n}{2}} (ωnk)2=ω2nk;
d. ω n 1 k 1 ∗ ω n 2 k 2 = ω n 1 + n 2 k 1 + k 2 \omega^{k_1}_{n_1}*\omega^{k_2}_{n_2}=\omega^{k_1+k_2}_{n_1+n_2} ωn1k1∗ωn2k2=ωn1+n2k1+k2; -
快速傅里叶变换
终于进入正题了,写的我好辛苦啊!!!
1.应用:用于求多项式的乘积,甚至可以求 A ∗ B P r o b l e m A*B\ Problem A∗B Problem(雾)。
2.算法:Cooley-Tukey(分治)
一般求多项式的乘积用的是系数表示法 A = ∑ i = 0 n a i ∗ x i A=\sum^n_{i=0}a_i*x^i A=∑i=0nai∗xi,这样求多项式的乘积的时间复杂度就是 O ( n 2 ) O(n^2) O(n2),有点慢。
而FFT选用的是点值表示法 ( x 1 , y 1 ) , . . . , ( x n , y n ) (x_1,y_1),...,(x_n,y_n) (x1,y1),...,(xn,yn),多项式的乘积就是 ( x 1 , y a 1 ∗ y b 1 ) , . . . , ( x n , y a n ∗ y b n ) (x_1,y_{a_1}*y_{b_1}),...,(x_n,y_{a_n}*y_{b_n}) (x1,ya1∗yb1),...,(xn,yan∗ybn),时间复杂度是 O ( n ) O(n) O(n),好快啊!!!
接下来就是选择点值表达式中的点了。上面我们提到了单位复数根,它有很多优美的性质,我们就选它作为点横坐标啦(雾)。
那么: A ( ω n k ) = ∑ i = 0 n − 1 a i ∗ ω n k i A(\omega^k_n)=\sum^{n-1}_{i=0}a_i*\omega^{k_i}_n A(ωnk)=i=0∑n−1ai∗ωnki
把 A ( x ) A(x) A(x)的系数按奇偶分开,即:
A 0 ( x ) = a 0 + a 2 x + a 4 x 2 + . . . A_0(x)=a_0+a_2x+a_4x^2+... A0(x)=a0+a2x+a4x2+...
A 1 ( x ) = a 1 + a 3 x + a 5 x 2 + . . . A_1(x)=a_1+a_3x+a_5x^2+... A1(x)=a1+a3x+a5x2+...
A ( x ) = A 0 ( x 2 ) + x A 1 ( x 2 ) A(x)=A_0(x^2)+xA_1(x^2) A(x)=A0(x2)+xA1(x2)
有兴趣可以自己验证一下。
那么: A ( ω n k ) = ∑ i = 0 n 2 − 1 a 2 i ω n 2 k i + ω n k ∑ i = 0 n 2 − 1 a 2 i + 1 ω n 2 k i A(\omega^k_n)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}\omega^{2ki}_{n}+\omega^k_n\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}\omega^{2ki}_{n} A(ωnk)=i=0∑2n−1a2iωn2ki+ωnki=0∑2n−1a2i+1ωn2ki
当 k < n 2 k<\frac{n}{2} k<2n时:
A ( ω n k ) = ∑ i = 0 n 2 − 1 a 2 i ω n 2 k i + ω n k ∑ i = 0 n 2 − 1 a 2 i + 1 ω n 2 k i A(\omega^k_n)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}\omega^{ki}_{\frac{n}{2}}+\omega^k_n\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}\omega^{ki}_{\frac{n}{2}} A(ωnk)=i=0∑2n−1a2iω2nki+ωnki=0∑2n−1a2i+1ω2nki
A ( ω n k + n 2 ) = ∑ i = 0 n 2 − 1 a 2 i ω n 2 k i + ω n k ∑ i = 0 n 2 − 1 a 2 i + 1 ω n 2 k i A(\omega^{k+\frac{n}{2}}_n)=\sum^{\frac{n}{2}-1}_{i=0}a_{2i}\omega^{ki}_{\frac{n}{2}}+\omega^k_n\sum^{\frac{n}{2}-1}_{i=0}a_{2i+1}\omega^{ki}_{\frac{n}{2}} A(ωnk+2n)=i=0∑2n−1a2iω2nki+ωnki=0∑2n−1a2i+1ω2nki
每次代入规模减半,复杂度为 O ( n log n ) O(n\log n) O(nlogn) -
傅里叶逆变换
将点值表达式转化为系数表达式。 -
实现
1.递归实现(常数太大,不常用);
2.非递归实现:先位翻转(蝴蝶变换),再自底向上实现,常数较小。 -
代码
其实说了那么多,我也不知道自己在写什么,还是看代码吧。
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 10000005
using namespace std;
const double pi=acos(-1.0);
struct complex
{
double x,y;
complex(double xx=0,double yy=0){x=xx,y=yy;}
}a[maxn],b[maxn];
int n,m;
int lim=1,l,r[maxn];
complex operator+(complex a,complex b)
{
return complex(a.x+b.x,a.y+b.y);
}
complex operator-(complex a,complex b)
{
return complex(a.x-b.x,a.y-b.y);
}
complex operator*(complex a,complex b)
{
return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}//复数运算
void fft(complex *c,int flag)
{
for(int i=0;i<lim;++i)
{
if(i<r[i])
swap(c[i],c[r[i]]);
}//求出迭代序列
for(int mid=1;mid<lim;mid<<=1)
{
complex wn(cos(pi/mid),flag*sin(pi/mid));
for(int r=mid<<1,j=0;j<lim;j+=r)//r是右端点,j表示当前位置
{
complex w(1,0);
for(int k=0;k<mid;++k,w=w*wn)
{
complex x=c[j+k],y=w*c[j+mid+k];
c[j+k]=x+y;
c[j+mid+k]=x-y;
}
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<=n;++i)
scanf("%lf",&a[i].x);
for(int i=0;i<=m;++i)
scanf("%lf",&b[i].x);
while(lim<=n+m)
{
lim<<=1;
l++;
}
for(int i=0;i<lim;++i)
r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));//蝴蝶变换
fft(a,1);
fft(b,1);
for(int i=0;i<=lim;++i)
a[i]=a[i]*b[i];
fft(a,-1);//傅里叶逆变换
for(int i=0;i<=n+m;++i)
printf("%d ",(int)(a[i].x/lim+0.5));
return 0;
}
-
总结
形如求 c ( n ) = ∑ i = 1 n − 1 a [ i ] + b [ n − i ] c(n)=\sum^{n-1}_{i=1}a[i]+b[n-i] c(n)=∑i=1n−1a[i]+b[n−i]的式子适合用 f f t fft fft或 n t t ntt ntt解决。 -
例题
1.【模板】多项式乘法(FFT);
2.【模板】分治 FFT;
3.【模板】A*B Problem升级版(FFT快速傅里叶);
快速数论变换(NTT)
-
原根
若 g g g是 p p p的一个原根,则 g 0 , g 1 , . . . , g p − 1 ( m o d p ) g^0,g^1,...,g^{p-1}(mod\ p) g0,g1,...,gp−1(mod p)是 p − 1 p-1 p−1个非0数。 -
NTT
与FFT类似,只是有模,并且 ω n i \omega^i_n ωni变成了原根 g g g而已。 -
代码
改天再贴。
*斯特林数相关算法
由于太难了,有时间再写。



























 534
534

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








