排序算法

最新推荐文章于 2025-05-29 08:47:41 发布

fc_1015775395

最新推荐文章于 2025-05-29 08:47:41 发布

阅读量133

点赞数

分类专栏：算法文章标签：排序算法

本文链接：https://blog.youkuaiyun.com/qq_43008530/article/details/113796483

版权

算法专栏收录该内容

4 篇文章

订阅专栏

本文详细介绍了快速排序算法的原理与实现，包括递归和迭代两种方式，并讨论了其时间复杂度、空间复杂度及稳定性。在C++中，通过示例展示了如何运用快速排序，特别提到了处理大数据时的优化策略。此外，还对比了前序遍历和后序遍历在快速排序中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、快速排序

分治思想。

（1）步骤

快排步骤

(2)代码

递归（前序遍历）

class Solution {
public:
    vector<int> vec;
    vector<int> sortArray(vector<int>& nums) {
        vec = nums;
        quick_sort(0,nums.size()-1);
        return vec;
    }
    void quick_sort(int left,int right){
        if(left>=right) return;
        int pivot = partition(left,right);
        quick_sort(left,pivot-1);
        quick_sort(pivot+1,right);
    }
    int partition(int left,int right){
        int pivot=vec[left];
        int i=left,j=right;
        while(i<j){
            while(i<j && vec[j]>=pivot) --j;
            while(i<j && vec[i]<=pivot) ++i;
            if(i<j) swap(vec[i],vec[j]);
        }
        swap(vec[left],vec[i]);
        return i;
    }
};

迭代

class Solution {
public:
    vector<int> vec;    
    vector<int> sortArray(vector<int>& nums) {
        vec=nums;
        stack<pair<int,int>> s;//类型由quick_sort()函数的参数决定
        s.push({0,vec.size()-1});
        while(!s.empty()){
            auto [low,high]=s.top();
            s.pop();
            int pos=partition(low,high);
            if(low<pos-1) s.push({low,pos-1});
            if(pos+1<high) s.push({pos+1,high});
        }
        return vec;
    }
    int partition(int low,int high){
        int pivot=vec[low];
        int i=low,j=high;
        while(i<j){
            while(i<j && vec[j]>=pivot) --j;
            while(i<j && vec[i]<=pivot) ++i;
            if(i<j) swap(vec[i],vec[j]);
        }
        swap(vec[low],vec[i]);
        return i;
    }
}

特殊处理
当取左右端点超时时，可以使用随机值或者中间值来与第一个元素交换，然后再取左端点作为基准。

swap(nums[left],nums[rand()%(right-left+1)+left]);
int pivot = nums[left];

复杂度
时间：平均O(nlogn)

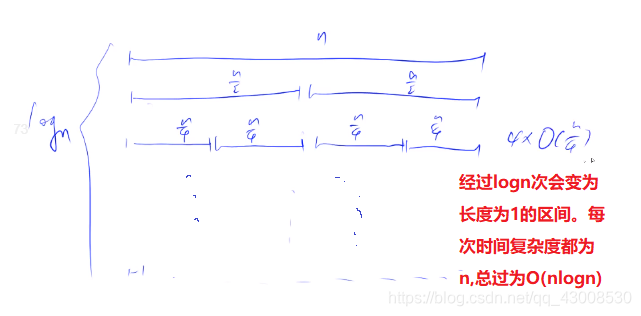
空间：O(logn)
稳定性：不稳定
变为稳定的方法：使用pair来存储值和索引，二个判断。

在C++中，当输入的数据比较多时，最好使用scanf来输入，不要使用cin来输入。

2、快速排序

分治思想。

（1）步骤

在这里插入图片描述

(2)代码

递归（后序遍历）

class Solution {
public:
    vector<int> res;//临时存放，然会再合并到原数组
    vector<int> sortArray(vector<int>& nums) {
        res.resize(nums.size(),0);
        merge_sort(nums,0,nums.size()-1);//[0,size] 
        return nums;   
    }
    void merge(vector<int>& nums,int first,int last,int mid){
        int i=first,j=mid+1,k=0;
        while(i<=mid && j<=last) res[k++]=nums[i]<nums[j]?nums[i++]:nums[j++];
        while(i<=mid) res[k++]=nums[i++];
        while(j<=last) res[k++]=nums[j++];
        for(int i=0;i<last-first+1;++i) nums[i+first]=res[i];
    }
    void merge_sort(vector<int>& nums,int first,int last){
        if(first>=last) return;
        int mid=first+(last-first)/2;
        merge_sort(nums,first,mid);
        merge_sort(nums,mid+1,last);
        merge(nums,first,last,mid);
    }
}

迭代

class Solution {
public:
    vector<int> tmp;
    vector<int> sortArray(vector<int>& nums) {
        tmp.resize(nums.size(),0);
        mergesort(nums,0,nums.size()-1);
        return nums;
    }
    void mergesort(vector<int>& nums,int first,int last){
        stack<pair<int,int>> s;//用来存放区间范围
        stack<tuple<int,int,int>> ss;//用来存放left，right，mid的
        if(first<last) s.push({first,last});
        while(!s.empty()){
            auto [left,right] = s.top();
            s.pop();
            int mid = left+(right-left)/2;
            ss.push({left,right,mid});
            if(left<mid) s.push({left,mid});
            if(mid+1<right) s.push({mid+1,right});
        }
        while(!ss.empty()){
            auto [left,right,mid] = ss.top();
            ss.pop();
            merge(nums,left,right,mid);
        }
    }
    void  merge(vector<int>& nums,int first,int last,int mid){
        int i=first,j=mid+1,k=0;
        while(i<=mid && j<=last) tmp[k++]=nums[i]>nums[j]?nums[j++]:nums[i++];
        while(i<=mid) tmp[k++]=nums[i++];
        while(j<=last) tmp[k++]=nums[j++];
        for(int i=0;i<k;++i){
            nums[first+i]=tmp[i];
        } 
    }
};