输入:
第一行:前序遍历序列
第二行:中序遍历序列
输出:
后序遍历序列
#include<iostream>
#include<cstring>
using namespace std;
struct Node{
Node *lchild;
Node *rchild;
char c;
}Tree[50];
int loc;//静态数组中已经分配的结点个数
Node *creat(){
Tree[loc].lchild=Tree[loc].rchild=NULL;//初始化左右儿子为空
return &Tree[loc++];
}
char str1[30],str2[30];//保存前序中序遍历结果字符串
void postOrder(Node *T){
if(T->lchild!=NULL){
postOrder(T->lchild);
}
if(T->rchild!=NULL){
postOrder(T->rchild);
}
cout<<T->c;
}
Node *build(int s1,int e1,int s2,int e2){//由字符串的前序遍历和中序遍历还原树,并返回其根节点,其中前序遍历结果为
//由str[s1]到str[e1],中序遍历结果为str[s2]到str2[e2]
Node* ret=creat();
ret->c=str1[s1];
int rootIdx;
for(int i=s2;i<=e2;i++){//查找该根节点字符在中序遍历中的位置
if(str2[i]==str1[s1]){
rootIdx=i;
break;
}
}
if(rootIdx!=s2){
ret->lchild=build(s1+1,s1+(rootIdx-s2),s2,rootIdx-1);
}
if(rootIdx!=e2){
ret->rchild=build(s1+rootIdx-s2+1,e1,rootIdx+1,e2);
}
return ret;//返回根节点指针
}
int main(){
while(cin>>str1){
cin>>str2;
loc=0;
int L1=strlen(str1);
int L2=strlen(str2);
Node *T=build(0,L1-1,0,L2-1);//还原整棵树将根节点保存在T中
postOrder(T);
cout<<endl;
}
return 0;
}
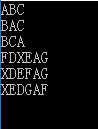








 博客介绍了一个算法问题,输入为树的前序遍历序列和中序遍历序列,输出为该树的后序遍历序列,聚焦于树的遍历算法相关信息技术内容。
博客介绍了一个算法问题,输入为树的前序遍历序列和中序遍历序列,输出为该树的后序遍历序列,聚焦于树的遍历算法相关信息技术内容。
















 767
767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








