一些ML名词

沟壑星空qq_42946961

已于 2022-06-08 18:42:06 修改

阅读量465

点赞数

文章标签： python

于 2021-11-18 20:38:34 首次发布

原文链接：https://blog.youkuaiyun.com/zhaoyu106/article/details/52292606

版权

评价指标

判别模型(Discriminative Model)和生成模型(Generative Model)

10折交叉验证

Leave-one-out cross-validation(LOOCV)

预处理和缩放：StandardScaler、RobustScaler、MinMaxScalar、Normalizer

评价指标

１)真正例(truepositive,TP):预测为正,实际为正;
２)真负例(truenegative,TN):预测为负,实际为负;
３)假正例(falsepositive,FP):预测为正,实际为负;
４)假负例(falsenegative,FN):预测为负,实际为正;
５)准确率:被正确分类的样本占所有样本的比例;
６)查准率:预测出的正例中真正例所占比例;
７)查全率或召回率:预测出的真正例占实际所有正例的比例;
８)误报率:预测出的假正例占实际所有负例的比例;
９)F-score:是对查准率和查全率的综合评价.
此外,对于二分类问题,本文还用受试者工作特征(receiveroperatingcharacteristic,ROC)曲线来分析检测性能;对于多分类问题,则使用混淆矩阵来直观地展示最终的检测结果。

判别模型(Discriminative Model)和生成模型(Generative Model)

原文：https://blog.youkuaiyun.com/zhaoyu106/article/details/52292606

一个通俗易懂的解释，摘录如下：

Let’s say you have input data x and you want to classify the data into labels y. A generative model learns the joint probability distribution p(x,y) and a discriminative model learns the conditional probability distribution p(y|x) - which you should read as ‘the probability of y given x’.

输入数据x，想把数据分类为标签y。生成模型学习联合分布概率判别模型学习条件概率分布-给定x，y的概率。

Here’s a really simple example. Suppose you have the following data in the form (x,y):

(1,0), (1,0), (2,0), (2, 1)

p(x,y) is

         y=0   y=1
        -----------
   x=1 | 1/2   0
   x=2 | 1/4   1/4

p(y|x) is

         y=0   y=1
        -----------
   x=1 | 1     0
   x=2 | 1/2   1/2

If you take a few minutes to stare at those two matrices, you will understand the difference between the two probability distributions.

花些时间比较这两个矩阵即可明白两个概率分布的区别。

The distribution p(y|x) is the natural distribution for classifying a given example x into a class y, which is why algorithms that model this directly are called discriminative algorithms. Generative algorithms model p(x,y), which can be tranformed into p(y|x) by applying Bayes rule and then used for classification. However, the distribution p(x,y) can also be used for other purposes. For example you could use p(x,y) to generate likely (x,y) pairs.

From the description above you might be thinking that generative models are more generally useful and therefore better, but it’s not as simple as that. This paper is a very popular reference on the subject of discriminative vs. generative classifiers, but it’s pretty heavy going. The overall gist is that discriminative models generally outperform generative models in classification tasks.

另一个解释，摘录如下：

判别模型Discriminative Model，又可以称为条件模型，或条件概率模型。估计的是条件概率分布(conditional distribution)， p(class|context)。
生成模型Generative Model，又叫产生式模型。估计的是联合概率分布（joint probability distribution），p(class, context)=p(clas

10折交叉验证

https://www.cnblogs.com/lpgit/p/9735102.html

构建一个分类器，输入为运动员的身高、体重，输出为其从事的体育项目-体操、田径或篮球。

一旦构建了分类器，我们就可能有兴趣回答类似下述的问题：

1. 该分类器的精确率怎么样？
2. 该分类器到底有多好？
3. 和其他分类器相比较，该分类器表现如何？

我们把每个数据集分成两个子集
    - 一个用于构建分类器，该数据集称为训练集（training set）
    - 另一个数据集用于评估分类器，该数据集称为测试集（test set）
    训练集和测试集是数据挖掘中的常用术语。

下面以近邻算法为例来解释为什么不能使用训练数据来测试。如果上述例子中的篮球运动员Marissa Coleman在训练数据中存在，那么身高6英尺1英寸体重160磅的她就会与自己最近。因此，如果对近邻算法进行评估时，若测试集是训练数据的子集，那么精确率总是接近于100%。更一般地，在评估任意数据挖掘算法时，如果测试集是训练数据的子集，那么结果就会十分乐观并且过度乐观。因此，这种做法看起来并不好。

那么我们将数据集分成两部分。较大的那部分用于训练，较小的那部分用于评估。事实表明这种做法也存在问题。在进行数据划分时可能会极端不走运。例如，所有测试集中的篮球运动员都比较矮（像Debbie Black的身高只有5英尺3英寸，体重只有124磅），他们会被分成马拉松运动员。而测试集中所有的田径运动员就像Tatyana Petrova（俄罗斯马拉松运动员，身高5英尺3英寸，体重108磅）一样较矮、体重较轻，可能会被分成体操运动员。如果测试集像上面一样，分类器的精确率会很差。另一方面，有时候测试集的选择又会十分幸运。测试集中的每个人都有所从事项目的标准身高和体重，此时分类器精确率接近100%。两种情况下，精确率都依赖于单个的测试集，并且该测试集可能并不能反映分类器应用于新数据的真实精确率。

上述问题的一种解决方法是重复多次上述过程并对结果求平均。例如，我们可以将数据分成两半：Part 1和Part 2。

我们可以使用Part 1的数据来训练分类器，而利用Part 2的数据对分类器进行测试。然后，我们重复上述过程，这次用Part 2训练而用Part 1测试。最后我们将两次的结果进行平均。但是，这种方法的问题在于我们每次只使用了一半数据进行训练。然而，我们可以通过增加划分的份数来解决这个问题。例如，我们可以将数据划分成3部分，每次利用2/3的数据训练而在其余1/3的数据上进行测试。因此，整个过程看起来如下：

第一次迭代使用Part 1和Part 2训练，使用Part 3测试

第二次迭代使用Part 1和Part 3训练，使用Part 2测试

第三次迭代使用Part 2和Part 3训练，使用Part 1测试

对上述结果求平均。

在数据挖掘中，最常用的划分数目是10，这种方法称为

10折交叉验证（10-fold Cross Validation）

使用这种方法，我们将数据集随机分成10份，使用其中9份进行训练而将另外1份用作测试。该过程可以重复10次，每次使用的测试数据不同。

10折交叉验证的例子

第1步，将数据等分到10个桶中。

我们会将50名篮球运动员和50名非篮球运动员分到每个桶中。每个桶当中放入了100人的信息。

第2步，下列步骤重复10次。

（1）每一次迭代中留存其中一个桶。第一次迭代中留存桶1，第二次留存桶2，其余依此类推。

（2）用其他9个桶的信息训练分类器（第一次迭代中利用从桶2到桶10的信息训练分类器）。

（3）利用留存的数据来测试分类器并保存测试结果。在上例中，这些结果可能如下：

35个篮球运动员被正确分类；

29个非篮球运动员被正确分类。

第3步，对上述结果汇总。

通常情况下我们会将结果放到与下表类似的表格中：

在所有500名篮球运动员中，有372人被正确分类。可能需要做的一件事是将右下角的数字也加上去，也就是说1000人当中有652（372+280）人被正确分类。因此得到的精确率为65.2%。与2折或3折交叉验证相比，基于10折交叉验证得到的结果可能更接近于分类器的真实性能。之所以这样，是因为每次采用90%而不是2折交叉验证中仅仅50%的数据来训练分类器。

有个问题
如果10折交叉验证之所以好只是因为采用了90%数据的话
那么为什么不用n折交叉验证？（n是数据集中样本的数目）

例如，如果数据集中包含1000个样本，我们可以在999个样本上训练分类器
然后在另外一个样本上测试分类器，这个过程可以重复1000次
利用这种最大可能的交叉验证次数，可能会得到更精确的分类器

留一法

在机器学习领域，n折交叉验证（n是数据集中样本的数目）被称为留一法。我们已经提到，留一法的一个优点是每次迭代中都使用了最大可能数目的样本来训练。另一个优点是该方法具有确定性。

确定性的含义

假设Lucy集中花费了80个小时来编写一个新分类器的代码。现在是周五，她已经筋疲力尽，于是她请她的两个同事（Emily和Li）在周末对分类器进行评估。她将分类器和相同的数据集交给每个人，请她们做10折交叉验证。周一，她问两人的结果……

嗯，她们得到了不同的结果。她们俩可能是谁犯错了吗？未必如此。在10折交叉验证中，我们随机将数据分到桶中。由于随机因素的存在，有可能Emily和Li的数据划分结果并不完全一致。实际上，她们划分一致的可能性微乎其微。因此，她们在训练分类器时，所用的训练数据并不一致，而在测试时所用的数据也不完全一致。因此，她们得到不同的结果是很符合逻辑的。该结果与是否由两个不同的人进行评估毫无关系。即使Lucy自己进行两次10折交叉验证，她得到的结果也会有些不同。之所以不同的原因在于将数据划分到桶这个过程具有随机性。由于10折交叉验证不能保证每次得到相同的结果，因此它是一种非确定性的方法。与此相反，留一法是确定性的。每次应用留一法到同一分类器及同一数据上，得到的结果都一样。这是件好事！

Leave-one-out cross-validation(LOOCV)

原文链接：https://blog.youkuaiyun.com/rocling/article/details/93336487

对上一段的补充。像Test set approach一样，LOOCV方法也包含将数据集分为训练集和测试集这一步骤。但是不同的是，我们现在只用一个数据作为测试集，其他的数据都作为训练集，并将此步骤重复N次（N为数据集的数据数量）。

如上图所示，假设我们现在有n个数据组成的数据集，那么LOOCV的方法就是每次取出一个数据作为测试集的唯一元素，而其他n-1个数据都作为训练集用于训练模型和调参。结果就是我们最终训练了n个模型，每次都能得到一个MSE。而计算最终test MSE则就是将这n个MSE取平均。

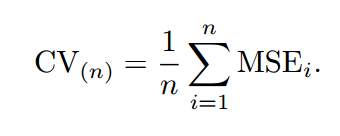
yi比起test set approach，LOOCV有很多优点。首先它不受测试集合训练集划分方法的影响，因为每一个数据都单独的做过测试集。同时，其用了n-1个数据训练模型，也几乎用到了所有的数据，保证了模型的bias更小。不过LOOCV的缺点也很明显，那就是计算量过于大，是test set approach耗时的n-1倍。

为了解决计算成本太大的弊端，又有人提供了下面的式子，使得LOOCV计算成本和只训练一个模型一样快。

其中表示第i个拟合值，而则表示leverage。关于的计算方法详见线性回归的部分（以后会涉及）。

2.2 K-fold Cross Validation

另外一种折中的办法叫做K折交叉验证，和LOOCV的不同在于，我们每次的测试集将不再只包含一个数据，而是多个，具体数目将根据K的选取决定。比如，如果K=5，那么我们利用五折交叉验证的步骤就是：

1.将所有数据集分成5份

2.不重复地每次取其中一份做测试集，用其他四份做训练集训练模型，之后计算该模型在测试集上的

3.将5次的取平均得到最后的MSE

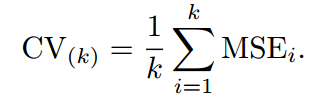
不难理解，其实LOOCV是一种特殊的K-fold Cross Validation（K=N）。再来看一组图：

每一幅图种蓝色表示的真实的test MSE，而黑色虚线和橙线则分贝表示的是LOOCV方法和10-fold CV方法得到的test MSE。我们可以看到事实上LOOCV和10-fold CV对test MSE的估计是很相似的，但是相比LOOCV，10-fold CV的计算成本却小了很多，耗时更少。

2.3 Bias-Variance Trade-Off for k-Fold Cross-Validation

最后，我们要说说K的选取。事实上，和开头给出的文章里的部分内容一样，K的选取是一个Bias和Variance的trade-off。

K越大，每次投入的训练集的数据越多，模型的Bias越小。但是K越大，又意味着每一次选取的训练集之前的相关性越大（考虑最极端的例子，当k=N，也就是在LOOCV里，每次都训练数据几乎是一样的）。而这种大相关性会导致最终的test error具有更大的Variance。

一般来说，根据经验我们一般选择k=5或10。

2.4 Cross-Validation on Classification Problems

上面我们讲的都是回归问题，所以用MSE来衡量test error。如果是分类问题，那么我们可以用以下式子来衡量Cross-Validation的test error：

其中Erri表示的是第i个模型在第i组测试集上的分类错误的个数。

图片来源：《An Introduction to Statistical Learning with Applications in R》

预处理和缩放：StandardScaler、RobustScaler、MinMaxScalar、Normalizer

原文链接：https://blog.youkuaiyun.com/weixin_43931465/article/details/107541247

这是一个有两个特征(x/y)的二分类数据集，四种预处理方法：

StandardScaler：确保每个特征的平均值为0，方差为1。
RobustScaler：使用中位数和四分位数（四分之一），确保每个特征的统计属性都位于同一范围。
MinMaxScalar：移动数据，使所有特征都刚好位于0-1之间。
Normalizer：对每个数据点进行缩放，使得特征向量的欧式长度等于1。

原文链接：https://blog.youkuaiyun.com/qq_42695322/article/details/113643014

而在了解使用网格搜索的原因之前，需要先了解一个名词——“参数”。

1.1 参数
参数，在程序里意义上来说就是一个变量。而在机器学习模型中，它大致可以分为两类：

超参数
在算法运行前需要决定的参数
模型参数
算法运行过程中学习的参数

以KNN模型为例，该模型是没有模型参数的，而k则是典型的超参数，因为在算法开始前就需要指定选取目标点的多少个邻居。
此外，若KNN中使用距离权重，且距离采用闵可夫斯基距离时，p也会成为一个超参数。

class是一个关键字，告诉系统我们要定义一个类,class后面加一个空格然后加类名。类名规则:首字母大写，如果多个单词用驼峰命名法，比如：KingMao,类名后面的小括号里是本类基于某个类定义，属于继承相关知识，暂时统一写object

类由三部分构成：

类的名称：类名

类的属性attribute

类的方法method

类对象支持两种操作：属性引用和实例化

class Dog(object): 类内部的代码属于对类型的描述，相当于刻画模版。类内部定义的函数一般称为方法

def eat(self, n):
    print('本汪吃了%d个苹果' % n)

类名后加小括号代表创建一个属于这个类型的对象（实例）

一个特殊的函数，当这个类型的某个对象被创建出的时候，会自动调用这个方法。通常这个特殊的方法，我们称之为构造方法（初始化方法）：

方法的类部包含两个属性name和age

def __init__(self, name, age):
    self.name = name 
    self.age = age def

两个下划线开头的函数是声明该属性为私有，不能在类的外部被使用或访问

__init__()方法又被称为构造器

https://easyai.tech/ai-definition/lstm/

Boosting采样和Bagging采样