Sklearn官方文档中文整理2——监督学习之线性和二次判别分析篇

1. 监督学习

1.2. 线性和二次判别分析【discriminant_analysis.LinearDiscriminantAnalysis和discriminant_analysis.QuadraticDiscriminantAnalysis】

Linear Discriminant Analysis（线性判别分析）(discriminant_analysis.LinearDiscriminantAnalysis) 和 Quadratic Discriminant Analysis （二次判别分析）(discriminant_analysis.QuadraticDiscriminantAnalysis) 是两个经典的分类器。 正如他们名字所描述的那样，他们分别代表了线性决策平面和二次决策平面。

这些分类器十分具有吸引力，因为他们可以很容易计算得到闭式解(即解析解)，其天生具有多分类的特性，在实践中已经被证明很有效，并且无需调参。

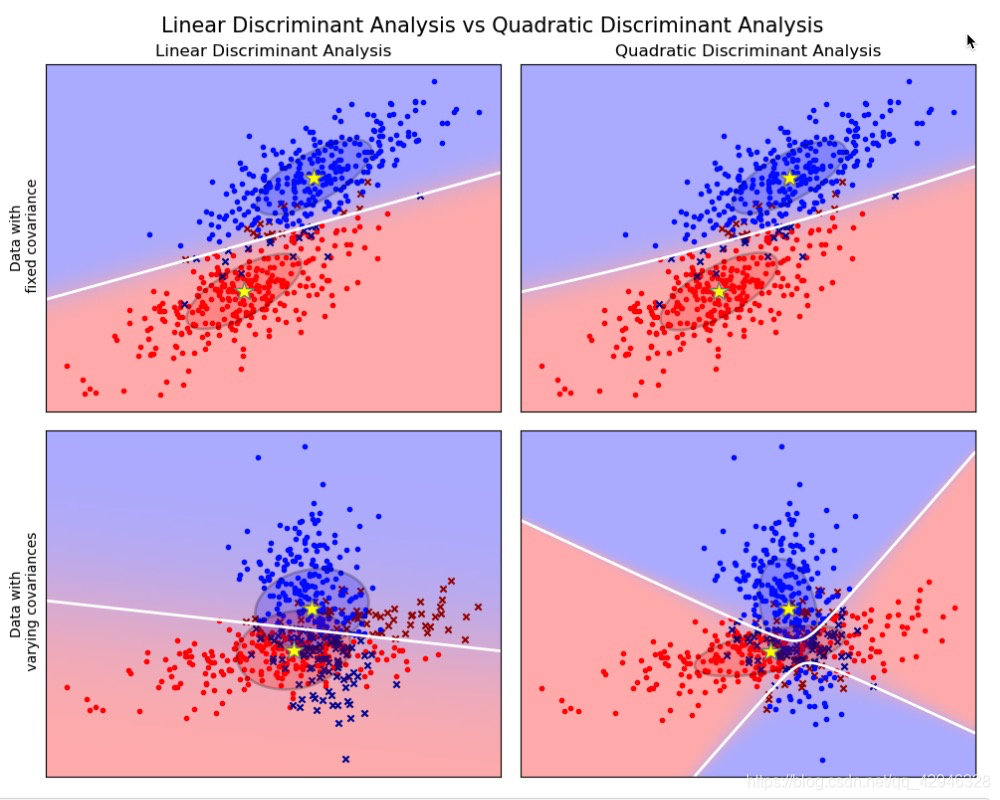
以上这些图像展示了 Linear Discriminant Analysis （线性判别分析）以及 Quadratic Discriminant Analysis （二次判别分析）的决策边界。其中，最后一行表明了线性判别分析只能学习线性边界， 而二次判别分析则可以学习二次边界，因此它相对而言更加灵活。

sklearn.discriminant_analysis.LinearDiscriminantAnalysis

参数	解释
solver:{‘svd’, ‘lsqr’, ‘eigen’}, default=’svd’	要使用的解算器，可能值：‘svd’: 奇异值分解（默认）。不计算协方差矩阵，因此建议对具有大量特征的数据使用此解算器。‘lsqr’:最小二乘解。可与收缩或自定义协方差估计相结合。‘eigen’: 特征值分解。可与收缩或自定义协方差估计相结合。
shrinkage：‘auto’ or float, default=None	收缩参数，可能值：None: 没有收缩（默认）。‘auto’: 用Ledoit-Wolf引理自动收缩。float between 0 and 1:固定收缩参数。如果使用协方差估计器，则应将其保留为“None”。请注意，收缩仅适用于“lsqr”和“eigen”解算器。
priors：array-like of shape (n_classes,), default=None	类先验概率。默认情况下，类比例是从训练数据中推断出来的。
n_components：int, default=None	用于降维的组件数量(<= min(n_classes - 1, n_features)) 。如果没有，将设置为min(n_classes - 1, n_features)。此参数仅影响变换方法。
store_covariance：bool, default=False	如果为True，则当解算器为“svd”时，明确计算类内加权协方差矩阵。矩阵总是为其他解算器计算和存储的。
tol：float, default=1.0e-4	将X的奇异值视为有效的绝对阈值，用于估计X的秩。将丢弃奇异值为非有效的维数。仅当解算器为“svd”时使用。
covariance_estimator：covariance estimator, default=None	如果不是None，则使用covariance_estimator来估计协方差矩阵，而不是依赖经验协方差估计量（具有潜在的收缩）。对象应该有一个拟合方法和一个协方差属性，如sklearn.covariance的估计器。 如果没有，收缩参数驱动估计。如果使用收缩率，则应将其保留为“None”。注意协方差估计只适用于lsqr和特征解算器。

属性	解释
coef_：ndarray of shape (n_features,) or (n_classes, n_features)	权重向量
intercept_：ndarray of shape (n_classes,)	截距项
covariance_：array-like of shape (n_features, n_features)	类内加权协方差矩阵。它对应于$su{m}_{k}prio{r}_k\ast C_k$其中$C_k$是k类样本的协方差矩阵。$C_k$使用协方差的（潜在收缩）有偏估计量来估计。如果解算器为“svd”，则仅当store_covariance为True时才存在。
explained_variance_ratio_：ndarray of shape (n_components,)	由每个所选组成部分解释的方差百分比。如果未设置n_components，则存储所有分量，解释的方差之和等于1.0。仅当使用eigen或svd解算器时可用。
means_：array-like of shape (n_classes, n_features)	Class-wise means.
priors_：array-like of shape (n_classes,)	类优先级（总和为1）。
scalings_：array-like of shape (rank, n_classes - 1)	类质心所跨越的空间中特征的缩放。仅适用于“svd”和“特征”解算器。
xbar_：array-like of shape (n_features,)	总体平均值。仅当“解算器”为“svd”时才存在。
classes_：array-like of shape (n_classes,)	唯一的类标签。

方法	解释
decision_function(X)	对样本数组应用决策函数。
fit(X, y[, sample_weight])	拟合模型
fit_transform(X[, y])	拟合数据再转换它
get_params([deep])	获取此估计器的参数。
predict(X)	预测
predict_log_proba(X)	估计对数概率。
predict_proba(X)	估计概率
score(X, y[, sample_weight])	返回给定测试数据和标签的平均精度。
set_params(**params)	设置此估计器的参数。
transform(X)	项目数据以最大化类分离。

例子：

>>> import numpy as np
>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = LinearDiscriminantAnalysis()
>>> clf.fit(X, y)
LinearDiscriminantAnalysis()
>>> print(clf.predict([[-0.8, -1]]))
[1]

sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis

参数	解释
priors：array-like of shape (n_classes,), default=None	类先验概率。默认情况下，类比例是从训练数据中推断出来的。