机器学习算法理论与实践——线性判别分析(LDA)

一、基本思想

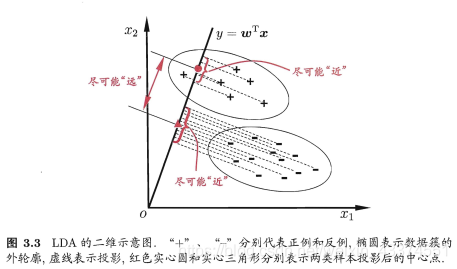
  线性判别分析(Linear Discriminant Analysis，简称 LDA)的思想：给定训练样例集，设法将样例投射到一条直线或一个超平面上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线或超平面上，再根据投影点的位置来确定新样本的类别。

二、数学推导

1.二分类

  给定数据集 D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } D=\{(x_i,y_i)\}_ {i=1}^m, y_i\in\{0,1\} D={ (xi​,yi​)}i=1m​,yi​∈{ 0,1}。令$X_i$表示样例集合，${\mu }_i$表示均值向量（${\mu }_1$表示$x\in X_1$的$x$的均值），${\sum }_i$表示协方差矩阵（${\sum }_0={\sum }_{x\in X_0}(x-{\mu }_0)(x-{\mu }_0{)}^T$），此处 i ∈ { 0 , 1 } i\in\{0,1\} i∈{ 0,1}。则两类样本的中心在直线上的投影为$w^T{\mu }_i$；两类样本所有点投射到直线上的协方差为$w^T{\sum }_{i}w$。

  投射的协方差推导过程：
由${\sum }_i={\sum }_{x\in X_i}(x_i-{\mu }_i)(x_i-{\mu }_i{)}^T$可得投射后的协方差${\sum }_i^{\prime }={\sum }_{x\in X_i}(w^T{x}_i-w^T{\mu }_i)(w^T{x}_i-w^T{\mu }_i{)}^T$，又