84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

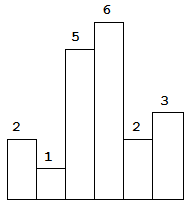
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

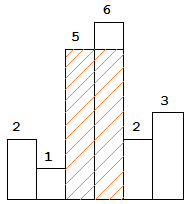
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：其实就是最大全1子矩阵，用单调栈求出以当前列为高向右向左所能扩展的边界，然后取一下最大值即可。
时间复杂度O（n），空间复杂度O（n）

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len=heights.length;
        int[] l=new int[len];
        int[] r=new int[len];
        int[] sta=new int[len];
        int cnt=0;
        for(int i=0;i<len;i++){
            while(cnt>0&&heights[sta[cnt-1]]>=heights[i]) cnt--;
            l[i]=cnt>0?sta[cnt-1]+1:0;
            sta[cnt++]=i;
        }
        cnt=0;
        for(int i=len-1;i>=0;i--){
            while(cnt>0&&heights[sta[cnt-1]]>=heights[i]) cnt--;
            r[i]=cnt>0?sta[cnt-1]-1:len-1;
            sta[cnt++]=i;
        }
        int ans=0;
        for(int i=0;i<len;i++){
            ans=Math.max(ans,heights[i]*(r[i]-l[i]+1));
        }
        return ans;
    }
}