带宽（Bandwidth, UVa 140）

最新推荐文章于 2019-09-01 17:58:09 发布

Nicolas Lee

最新推荐文章于 2019-09-01 17:58:09 发布

阅读量911

点赞数 1

CC 4.0 BY-SA版权

分类专栏：暴力搜索 c++ 算法竞赛入门经典（第二版）文章标签：递归回溯解答树剪枝 UVA

本文链接：https://blog.youkuaiyun.com/qq_42835910/article/details/86295181

算法竞赛入门经典（第二版）同时被 3 个专栏收录

100 篇文章

订阅专栏

暴力搜索

46 篇文章

订阅专栏

c++

32 篇文章

订阅专栏

探讨了在给定图G中寻找使带宽最小化的结点排列算法，通过剪枝技术减少全排列搜索的空间，有效提升求解效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

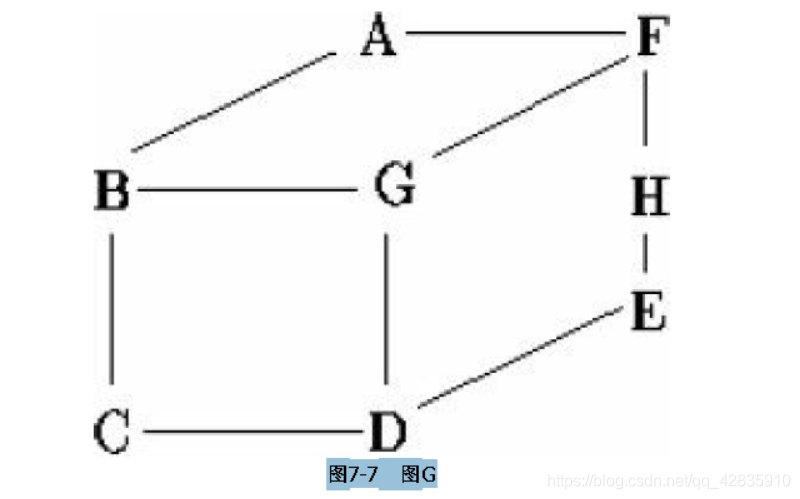
给出一个n（n≤8）个结点的图G和一个结点的排列，定义结点i的带宽b(i)为i和相邻结点在排列中的最远距离，而所有b(i)的最大值就是整个图的带宽。给定图G，求出让带宽最小的结点排列，如图7-7所示。

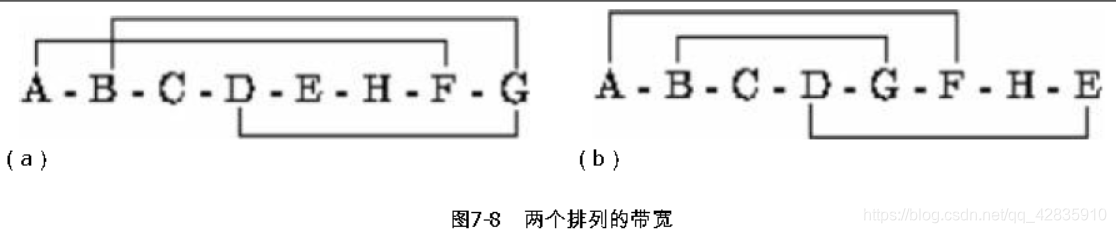
下面两个排列的带宽分别为6和5。具体来说，图7-8（a）中各个结点的带宽分别为6, 6,1, 4, 1, 1, 6, 6，图7-8（b）中各个结点的带宽分别为5, 3, 1, 4, 3, 5, 1, 4。

可以记录下目前已经找到的最小带宽res。如果发现已经有某两个结点的距离大于或等于res，再怎么扩展也不可能比当前解更优，应当强制把它“剪”掉，就像园丁在花园里为树修剪枝叶一样，也可以为解答树“剪枝（prune）”。

#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> v[26];
bool ch[26]; 
int ans[10],id[10];
int main(int argc, char** argv) {
	string line;
	while(cin>>line && line[0]!='#'){
		for(int i=0;i<26;i++) v[i].clear();
		memset(ch,0,sizeof(ch));
		for(int i=0,j,len=line.length();i<len;i++){
			ch[line[i]-'A']=true;
			for(j=i+2;j<len && line[j]!=';';j++){
                //确定了A到B的，自然就确定了B到A的。
				v[line[i]-'A'].push_back(line[j]-'A');
				ch[line[j]-'A']=true;
			}
			i=j;
		}
		int n=0;
		for(int i=0;i<26;i++) if(ch[i]) id[n++]=i;
		int res=n;
		do{
			int maxn=0;
			for(int i=0;i<n;i++){
				for(int j=0,len=v[id[i]].size();j<len;j++){
					for(int k=0;k<n;k++){
						if(id[k]==v[id[i]][j]) {
							maxn=max(maxn,abs(k-i));							
							break;
						}
					}
					if(maxn>=res) break;//已经大于等于最优解,剪枝  
				}
				if(maxn>=res) break;
			}
			if(res>maxn){
				memcpy(ans,id,sizeof(id));
				res=maxn;
			}
		}while(next_permutation(id,id+n));//库函数枚举全排列 
		for(int i=0;i<n;i++)
			cout<<char(ans[i]+'A')<<" ";					
		cout<<"-> "<<res<<endl;
	}
	return 0;
}

没有使用库函数代码：代码繁琐一点。

#include <iostream>
#include <string>
#include <cstring>
#include <vector>
#include <cmath>
using namespace std;
vector<int> v[26];
int n,res;
bool ch[26],use[10];
int t[10],ans[10],id[10];
void add(string line){
	for(int i=0;i<26;i++) v[i].clear();
	memset(ch,0,sizeof(ch));
	for(int i=0,j,len=line.length();i<len;i++){
		ch[line[i]-'A']=true;
		for(j=i+2;j<len && line[j]!=';';j++){
			v[line[i]-'A'].push_back(line[j]-'A');
			ch[line[j]-'A']=true;
		}
		i=j;
	}
} 

void dfs(int cur){
	if(cur==n){
		int maxn=0;
		for(int i=0;i<n;i++){
			for(int j=0;j<v[t[i]].size();j++){
				for(int k=0;k<n;k++){
					if(t[k]==v[t[i]][j]) {						
						maxn=max(maxn,abs(i-k));
						if(maxn>=res) return;
						break;
					}
				}
			}
		}
		if(res>maxn){
			memcpy(ans,t,sizeof(t));
			res=maxn;
		}
		return;
	}
	for(int i=0;i<n;i++){
		if(!use[i] ){
			use[i]=true;
			t[cur]=id[i];
			dfs(cur+1);
			use[i]=false;
		}
	}
}


int main(int argc, char** argv) {
	string line;
	while(cin>>line && line[0]!='#'){
		add(line);
		n=0;
		for(int i=0;i<26;i++) if(ch[i]) id[n++]=i;
		res=n;
		dfs(0);	
		for(int i=0;i<n;i++){
			cout<<char(ans[i]+'A')<<" ";
		}					
		cout<<"-> "<<res<<endl;
	}
	return 0;
}