Python-深度学习-学习笔记（11）：构建单层神经网络（步骤 + 代码）

Python-深度学习-学习笔记（11）：构建单层神经网络（步骤 + 代码）

单层神经网络包括：输入层 -> 输出层

多层神经网络包括：输入层 -> 隐蔽层 -> 输出层

1.标准化

首先针对于一些数据值相差过大的情况，我们要采用一些方法（指数化、除以相同分母等）使其元素的值集中在一个较小的范围，能够使计算结果更有意义。
这一步在我们加载数据之前进行。

2.前向传播

2.1构建sigmoid函数

Sigmoid函数之所以叫Sigmoid，是因为函数的图像很像一个字母S。sigmoid函数即为logistic回归方程，此函数一般用在聚类分类问题中，因为有良好的“对与错”性质，能够很好地将结果分为两类。

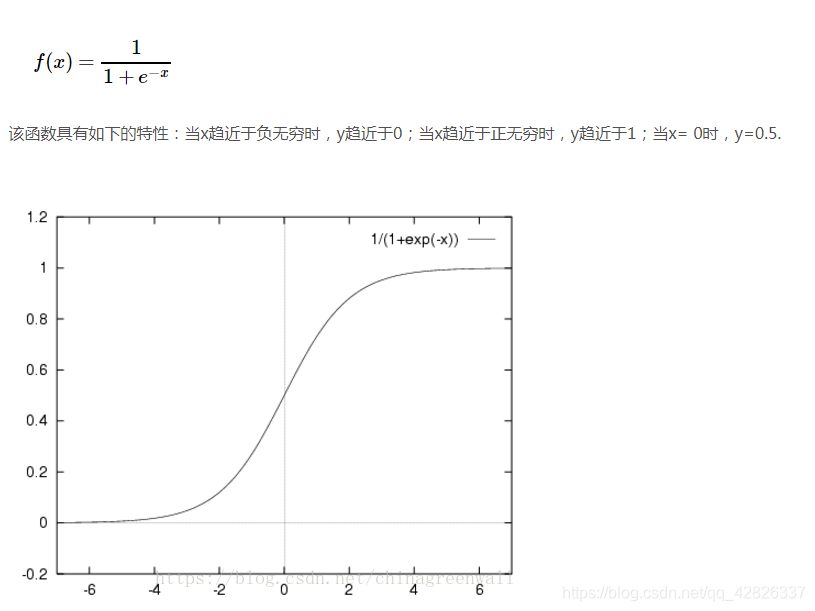
代码：

def sigmoid(z):
    """
    参数：
        z  - 任何大小的标量或numpy数组。

    返回：
        s  -  sigmoid（z）
    """
    s = 1 / (1 + np.exp(-z))
    return s

2.2 初始化参数

在构建前向传播时，我们遇到的最常见的两个参数是w和b，其中w是控制斜率，b控制平移方向，类似于我们学过的线性方程，神经网络的最终目的就是要无限趋近于一对w和b的值，使最终的结果最接近理想结果（也可以说是使代价函数的值最小）。

w叫做权重，b叫做偏差数。

代码：

def initialize_with_zeros(dim):
    """
        此函数为w创建一个维度为（dim，1）的0向量，并将b初始化为0。

        参数：
            dim  - 我们想要的w矢量的大小（或者这种情况下的参数数量）

        返回：
            w  - 维度为（dim，1）的初始化向量。
            b  - 初始化的标量（对应于偏差）
    """
    w = np.zeros(shape = (dim,1)) #这里也可以设置一个随机值
    b = 0
    #使用断言来确保我要的数据是正确的
    assert(w.shape == (dim, 1)) #w的维度是(dim,1)
    assert(isinstance(b, float) or isinstance(b, int)) #b的类型是float或者是int

    return (w , b)

注：在初始化时，如果初始化权重都为0，那么所有隐藏单元都是对称的，梯度下降是没有意义的，所以一般采用随机初始化的方式。

2.3 前向传播

前向传播基本上就是由以下4个方程所组成：

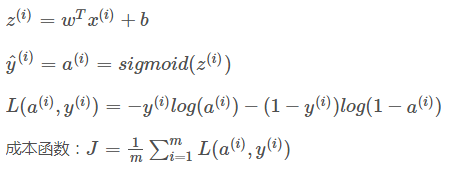
def forward_propagate(w, b, X, Y):
    """
    实现前向传播的成本函数及其梯度。
    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 矩阵类型为（num_px * num_px * 3，训练数量）
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据数量)
    返回：
        cost- 逻辑回归的负对数似然成本
       """
    m = X.shape[1]
           
    #正向传播
    A = sigmoid(np.dot(w.T,X) + b) #计算激活值，请参考公式2。
    cost = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A))) #计算成本，请参考公式3和4。
    
    #使用断言确保数据是正确的
    cost = np.squeeze(cost)
    assert(cost.shape == ())
    
	return (cost)  #返回一个代价函数的值，用来观察下降情况

3.后向传播

后向传播基本上就是由以下2个方程所组成：

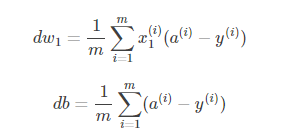
代码：

def backward_propagate(X, Y, A):
    """
    实现后向传播的成本函数及其梯度。
    参数：

        X  - 矩阵类型为（num_px * num_px * 3，训练数量）
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据数量)
        A  - 激活后的值 

    返回：
        dw  - 相对于w的损失梯度，因此与w相同的形状
        db  - 相对于b的损失梯度，因此与b的形状相同
    """
    #反向传播
    dw = (1 / m) * np.dot(X, (A - Y).T) #请参考视频中的偏导公式。
    db = (1 / m) * np.sum(A - Y) #请参考视频中的偏导公式。

    #使用断言确保我的数据是正确的
    assert(dw.shape == w.shape)
    assert(db.dtype == float)

    #创建一个字典，把dw和db保存起来。
    grads = {
                "dw": dw,
                "db": db
             }
    return (grads)

当然在推广到多隐藏层时，公式改变为如下：

4.参数优化

现在，我要使用渐变下降更新参数，用旧的w,b来更新参数，从而获得更新的w,b值，使得代价函数的值尽可能的小，实现最优解。

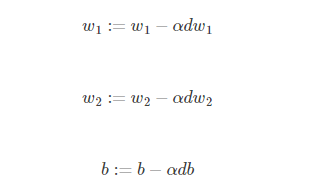
目标是通过最小化成本函数 J 来学习 w和b 。对于参数 θ ，更新规则是 θ=θ−α dθ，其中 α 是学习率。

这一步的重点在于把握学习速率，为了让渐变下降起作用，我们必须明智地选择学习速率。学习率α 决定了我们更新参数的速度。如果学习率过高，我们可能会“超过”最优值。同样，如果它太小，我们将需要太多迭代才能收敛到最佳值。这就是为什么使用良好调整的学习率至关重要的原因。

我们可以通过查看代价函数的值或者观察学习速率曲线来判断和更改学习速率和迭代次数。

代码：

def optimize(w , b , X , Y , num_iterations , learning_rate , print_cost = False):
    """
    此函数通过运行梯度下降算法来优化w和b

    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数组。
        Y  - 真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据的数量)
        num_iterations  - 优化循环的迭代次数
        learning_rate  - 梯度下降更新规则的学习率
        print_cost  - 每100步打印一次损失值

    返回：
        params  - 包含权重w和偏差b的字典
        grads  - 包含权重和偏差相对于成本函数的梯度的字典
        成本 - 优化期间计算的所有成本列表，将用于绘制学习曲线。

    提示：
    我们需要写下两个步骤并遍历它们：
        1）计算当前参数的成本和梯度，使用propagate（）。
        2）使用w和b的梯度下降法则更新参数。
    """

    costs = []

    for i in range(num_iterations):

        grads, cost = propagate(w, b, X, Y) #其中包括forward_propagate和backward_propagate

        dw = grads["dw"]
        db = grads["db"]

        w = w - learning_rate * dw
        b = b - learning_rate * db

        #记录成本
        if i % 100 == 0:
            costs.append(cost)
        #打印成本数据
        if (print_cost) and (i % 100 == 0):
            print("迭代的次数: %i ， 误差值： %f" % (i,cost))

    params  = {
                "w" : w,
                "b" : b }
    grads = {
            "dw": dw,
            "db": db } 
    return (params , grads , costs)

4.结果预测

optimize函数会输出已学习的w和b的值，我们可以使用w和b来预测数据集X的标签（这里是一个二元分类的例子）。

现在我们要实现预测函数predict（）。计算预测有两个步骤：

1. 计算a的值
2. 将a的值变为0（如果激活值<= 0.5）或者为1（如果激活值> 0.5）,然后将预测值存储在向量Y_prediction中。

代码:

def predict(w , b , X ):
    """
    使用学习逻辑回归参数logistic （w，b）预测标签是0还是1，

    参数：
        w  - 权重，大小不等的数组（num_px * num_px * 3，1）
        b  - 偏差，一个标量
        X  - 维度为（num_px * num_px * 3，训练数据的数量）的数据

    返回：
        Y_prediction  - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组（向量）

    """

    m  = X.shape[1] #图片的数量
    Y_prediction = np.zeros((1,m)) 
    w = w.reshape(X.shape[0],1)

    #计预测猫在图片中出现的概率
    A = sigmoid(np.dot(w.T , X) + b)
    for i in range(A.shape[1]):
        #将概率a [0，i]转换为实际预测p [0，i]
        Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
    #使用断言
    assert(Y_prediction.shape == (1,m))

    return Y_prediction

总结

建立神经网络的主要步骤：

1、定义模型结构（例如输入特征的数量）。

2、初始化模型参数。

3、进行循环训练

• 计算当前损失（前向传播）
• 计算当前梯度（后向传播）
• 更新参数（梯度下降）

通过循环更新参数实现梯度下降，从而获得最佳的w和b的值，使得代价函数J尽可能的小（这里不一定是训练次数越多越好，当训练次数达到一定值时，效果会减弱）。

补充：多层神经网络维度

---

W1 - 权重矩阵，维度为（n_h，n_x）
b1 - 偏向量 ，维度为（n_h，1）
W2 - 权重矩阵，维度为（n_y，n_h）
b2 - 偏向量，维度为（n_y，1）
X - 输入，维度为（n_x，m）

其中n_x为上一层输入节点数，n_h为隐蔽层节点数，n_y为输出层节点数。

---

例：假设有3个输入节点，4个隐蔽层节点，1个输出层节点

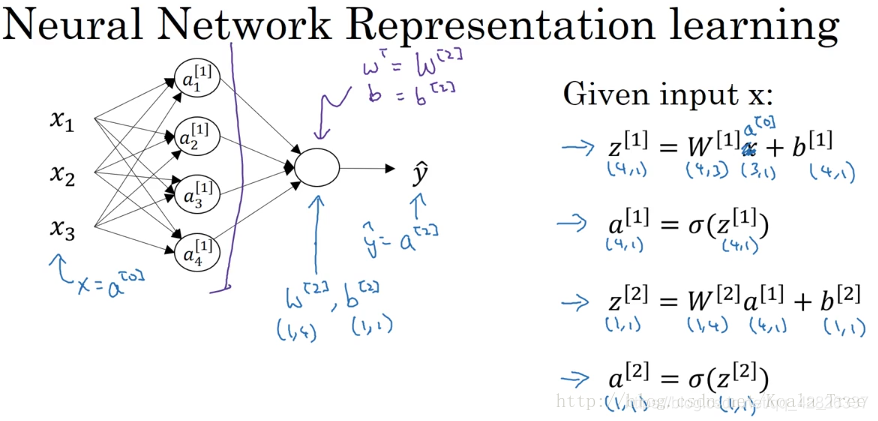
各自维度为：

W1 - 权重矩阵，维度为（4，3）
b1 - 偏向量 ，维度为（4，1）
W2 - 权重矩阵，维度为（1，4）
b2 - 偏向量，维度为（1，1）
X - 输入，维度为（3，m）