排序之归并排序

原创已于 2022-02-15 21:09:10 修改 · 587 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#排序算法 #算法 #数据结构

于 2022-02-15 21:08:05 首次发布

C/C++ 同时被 2 个专栏收录

49 篇文章

订阅专栏

算法

23 篇文章

订阅专栏

本文详细介绍了归并排序的原理，包括划分、排序和合并三个主要步骤，并通过具体的代码示例展示了如何使用递归实现归并排序。在代码部分，展示了核心的merge()函数和封装后的mergeSort()函数，以及测试用例的main函数，最终得出有序数组的输出结果。

归并排序

定义

归并排序是一种采用分治法，即先使每个子序列有序，再使子序列段间有序，然后合成一个完整的有序表的有效排序方法。

主要步骤

划分
排序
合并

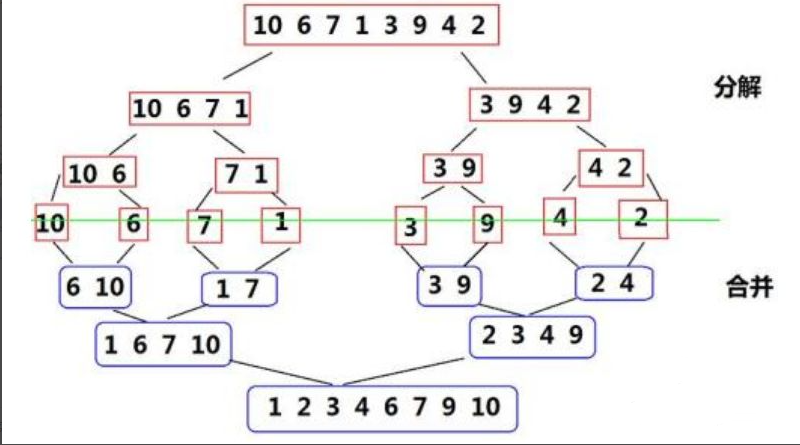
实际过程

实际过程如下图(图片来自百度)

归并排序

代码

核心代码

merge()

因为我们在此使用了递归的方式，对于临时数组temp在此函数内不好写，所以为了简洁我们不直接调用该函数，而是再次封装的mergeSort()

//R为排序数组,l为左界,r为右界,temp为临时数组
void merge(int R[],int l, int r,int temp[])
{
	//若左右边界相等则返回
	if (l == r) return;

	//中间位置，位运算右移1位相当于除以2
	int mid = (l + r) >> 1;

	//为保证[l,mid] [mid+1,r]有序性，我们在此先递归
	merge(R,l, mid,temp);
	merge(R,mid + 1, r,temp);

	//利用临时数组，并从左右区间开头一次取到最小，然后跳过这个数（逆序取大）
	int lp = l;			//左边区间取到的最小值
	int rp = mid + 1;	//右边区间取到的最小值
	int cnt = 0;		//选出的数的个数


	while (lp <= mid && rp <= r)
	{
		temp[cnt] = R[lp] < R[rp] ? R[lp++] : R[rp++];
		cnt++;
	}

	//若做有区间还有剩余的数，则依次把它们装入临时数组
	while (lp <= mid)
		temp[cnt] = R[lp], lp++, cnt++;
	while (rp <= r)
		temp[cnt] = R[rp], rp++, cnt++;

	//更新数组,register int是将其放到寄存器中以提高效率
	for (register int i = l; i <= r; i++)
		R[i] = temp[i - l];

}

mergeSort()

//R为排序数组,l为左界,r为右界
void mergeSort(int R[], int l, int r)
{
	if (l >= r) return;
	int* temp = (int*)malloc(r - l+1);
	merge(R, l, r, temp);
}

调用测试

main函数

int main()
{
	int num[] = { 5,4,3,2,1 };
	mergeSort(num,0, 4);
	for (int i = 0; i < 5; i++)
		cout << num[i] << endl;

	return 0;
}

输出结果