朴素贝叶斯

条件概率

•设A，B为任意两个事件，若P(A)>0，我们称在已知事件A发生的条件下，事件B发生的概率为条件概率，记为P(B|A)，并定义
$$P(B|A)=\frac{P(AB)}{P(A}$$

乘法公式

•如果P(A)>0，则P(AB)=P(A)P(B|A)

•如果P(A1…An-1)>0，则P(A1…An)= P(A1) P(A2|A1) P(A3|A1A2)…P(An|A1…An-1)

全概率公式

$$U_{i=1}^n{A}_i=\Omega ,A_i{A}_j=空集(一切i!=j)$$

•P(Ai)>0，则对任一事件B，有
$$P(B)=\sum _{i=1}^{n}P(A_i)P(B|A_i)$$
•全概率公式是用于计算某个“结果” B发生的可能性大小。如果一个结果B的发生总是与某些前提条件Ai 相联系，那么在计算P(B)时，我们就要用Ai 对B作分解，应用全概率公式计算P(B)，我们常称这种方法为全集分解法。

根据小偷们的资料，计算村子今晚失窃概率的问题：P(Ai)表示小偷 i 作案的概率，P(B|Ai)表示小偷
i 作案成功的概率，那么P(B)就是村子失窃的概率

贝叶斯公式（又称逆概公式）
$$U_{i=1}^n{A}_i=\Omega ,A_i{A}_j=空集(一切i!=j)$$
P(Ai)>0，则对任一事件B，只要P(B)>0，有
$$P(A_j|B)=\frac{p(A_{j}B)}{{\sum }_{i=1}^{n}P(A_i)P(B|A_i)}$$
•如果在B发生的条件下探求导致这一结果的各种“原因” Aj 发生的可能性大小P(Aj |B)，则要应用贝叶斯公式

若村子今晚失窃，计算哪个小偷嫌疑最大的问题（嫌疑最大就是后验概率最大）

假设小偷1和小偷2在某村庄的作案数量比为3:2，前者偷窃成功的概率为0.02，后者为0.01，现村庄失窃，求这次失窃是小偷1作案的概率。

【分析】A1={小偷1作案}，A2={小偷2作案}，B={村庄失窃}
$$\begin{gathered} P(A_1)=3/5,P(A_2) \\ P(B|A_1)=0.02,P(B|A_2)=0.01 \\ P(A_1|B)=\frac{p(A_{1}B)}{{\sum }_{i=1}^{2}P(A_i)P(B|A_i)}=3/4 \\ P(A_2|B)=\frac{p(A_{2}B)}{{\sum }_{i=1}^{2}P(A_i)P(B|A_i)}=1/4 \end{gathered}$$

总结:

先验概率P(A)：在不考虑任何情况下，A事件发生的概率
条件概率P(B|A)：A事件发生的情况下，B事件发生的概率
后验概率P(A|B)：在B事件发生之后，对A事件发生的概率的重新评估
全概率：如果A和A’构成样本空间的一个划分，那么事件B的概率为：A和A’的概率分别乘以B对这两个事件的概率之和。

朴素贝叶斯的直观理解

案例：

有一个训练集包含100个人，其中有60个非洲人（黑卷47,黑直1,黄卷11,黄直1），有40个亚洲人（黑卷1,黄卷4,黄直*35），请训练朴素贝叶斯模型。

肤色x1={黑，黄}， 发型x2={卷，直}； 地区label={亚，非}

先计算先验概率：

亚洲人的比例m，非洲人的比例
$$P(非洲)=\frac{60}{100},P(亚洲)=40/100$$
模型构建：根据资料计算模型参数

亚洲人中肤色=黑的比例，亚洲人中肤色=黄的比例

$$P(黑|亚洲)=1/40,P(黄|亚洲)=39/40$$
非洲人中肤色=黑的比例，非洲人中肤色=黄的比例
$$P(黑|非洲)=48/60,p(黄|非洲)=12/60$$
亚洲人中发型=卷的比例，亚洲人中发型=直的比例
$$P(卷|亚洲)=5/40,p(直|亚洲)=35/40$$
非洲人中发型=卷的比例，非洲人中发型=直的比例

$$P(卷|非洲)=58/60,p(直|非洲)=2/60$$

假设新来了一个人【[黑，卷]，地区=？】，请用朴素贝叶斯模型预测这个人的地区。Y表示地区，X表示特征向量，根据贝叶斯公式，并假设特征间独立的假设有：

$$P(Y|X)=\frac{P(Y)\ast P(X|Y)}{P(X)}{\to }^{朴素贝叶斯}P(Y|X)=\frac{P(Y)\ast P(X^{(1)}|Y)\ast P(X^{(2)}|Y)}{P(X)}$$

和特征间独立的假设（朴素），得
$$\begin{gathered} P(非洲|黑卷)=P(非洲)P(黑|非洲)P(卷|非洲)=\frac{60}{100}\frac{48}{60}\frac{58}{60} \\ P(亚洲|黑卷)=P(亚洲)P(黑|亚洲)P(卷|亚洲)=\frac{40}{100}\frac{1}{40}\frac{5}{40} \end{gathered}$$

根据计算结果，模型会将这个人的地区预测为非洲。

朴素：假设特征间是独立的（忽略肤色和发型的联系），从而变成了“低配版的贝叶斯模型”，称为“朴素贝叶斯”。

优点：是可以减少需要估计的参数的个数；缺点：会牺牲一定的分类准确率。

如果是贝叶斯模型的话，模型参数总数为：
len{亚洲,非洲}∗len{黑,黄}∗len{卷,直} len\{亚洲,非洲\}*len\{黑,黄\}*len\{卷,直\} len{亚洲,非洲}∗len{黑,黄}∗len{卷,直}
是指数增长的，实际是不可行的；而朴素贝叶斯模型参数总数为：
len{亚洲,非洲}∗(len{黑,黄}+len{卷,直}) len\{亚洲,非洲\}*(len\{黑,黄\}+len\{卷,直\}) len{亚洲,非洲}∗(len{黑,黄}+len{卷,直})
通过朴素贝叶斯就可以避免线性增长。

训练：先根据数据集，计算标记（地区）的先验概率，再计算每一个特征（肤色和发型）的条件概率，这些概率值就是模型参数，因此朴素贝叶斯的训练成本很低。

预测：当一个【黑，卷】来报道时，假设特征间是独立的，朴素贝叶斯模型会预测他的老家是非洲的，原理就是

“非洲人的概率 非洲人里肤色为黑的比例 非洲人里发型为卷的比例 > 亚洲人的概率 亚洲人里肤色为黑的比例 亚洲人里发型为卷的比例”。

朴素贝叶斯模型会将实例预测为后验概率最大的类。

继续上文的引例，考虑一个这样的问题：

假设某人的地区完全依靠其肤色的就能确定，发型是一个对判断地区没有参考价值的特征，假设P(卷|非洲)=0， P(卷|亚洲)=0.001，当来了一个【黑，卷】人的时候，我们算出
$$\begin{gathered} P(非洲)P(黑|非洲)P(卷|非洲)=0 \\ P(亚洲)P(黑|亚洲)P(卷|亚洲)=0.00001 \end{gathered}$$
然后被预测为亚洲人，傻了吧？

原因：出现某个模型参数为0时，0乘任何数都=0，直接影响到后验概率的计算结果。

解决这一问题的方法是使用平滑操作，改造先验概率公式：
P(非洲)=60+λ100+len{亚洲,非洲}∗λ=60+λ100+2∗λ P(非洲) = \frac{60+\lambda}{100+len\{亚洲,非洲\}*\lambda}=\frac{60+\lambda}{100+2*\lambda} P(非洲)=100+len{亚洲,非洲}∗λ60+λ​=100+2∗λ60+λ​
改造每个特征的条件概率公式（这里只列举了2个）：
P(黑∣非洲)=48+λ60+len{黑,白}∗λ=48+λ60+2∗λP(直∣非洲)=2+λ60+len{直,卷}∗λ=2+λ60+2∗λ P(黑|非洲) = \frac{48+\lambda}{60+len\{黑,白\}*\lambda}=\frac{48+\lambda}{60+2*\lambda}\\ P(直|非洲) = \frac{2+\lambda}{60+len\{直,卷\}*\lambda}=\frac{2+\lambda}{60+2*\lambda} P(黑∣非洲)=60+len{黑,白}∗λ48+λ​=60+2∗λ48+λ​P(直∣非洲)=60+len{直,卷}∗λ2+λ​=60+2∗λ2+λ​
在随机变量各个取值的频数上赋予一个正数，当λ=1时，称为拉普拉斯平滑

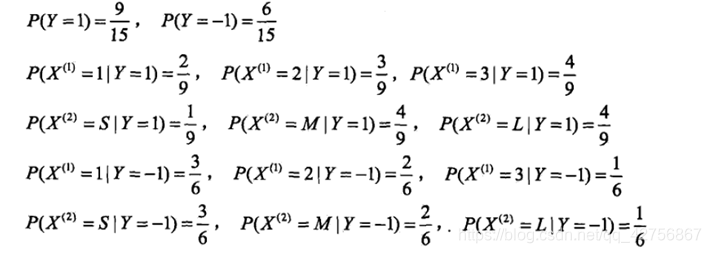
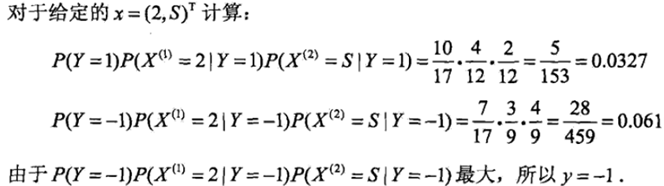
拉普拉斯平滑

$${\overline{\theta }}_{y_i}=\frac{N_{y_i}+\alpha }{N_y+{\alpha }_n}$$

17: 15+2 (拉普拉斯平滑)

10: 9+1 (拉普拉斯平滑)

代码实现

import pandas as pd

def tokey(col_name,category,y): #定义写key的函数,比如产生 'X1=3|Y=1'
    return col_name+"="+str(category)+"|Y="+str(y)

df = pd.read_csv("datas/bayes_lihang.txt")
lam = 1 #平滑因子
P = {} #用于存储所有概率的字典
Y = df["Y"].value_counts().keys() #获取类别种类的list
col_names = df.columns.tolist()[:-1] #获取特征列名
for y in Y: #遍历每个类别
    df2 = df[df["Y"]==y] #获取每个类别下的DF
    p = (df2.shape[0]+lam)/(df.shape[0]+len(Y)*lam) #计算先验概率
    P[y] = p #将先验概率加入P
    for col_name in col_names: #遍历每个特征
        categorys = df2[col_name].value_counts().keys() #获取每个特征下特征值种类的list
        for category in categorys: #遍历每个特征值
            p = (df2[df2[col_name]==category].shape[0]+lam)/(df2.shape[0]+len(categorys)*lam) #计算在某类别下，特征=某特征的条件概率
            P[tokey(col_name,category,y)] = p  #将条件概率加到P
print(P) 
X = [2,"S"] #待测数据
res = []  #用于存储属于某一类别的后验概率
for y in Y: #遍历类别
    p = P[y] #获取先验概率
    for i in range(len(X)): #遍历特征
        p*=P[tokey(col_names[i],X[i],y)]  #获取条件概率
    print(p)
    res.append(p)  #将后验概率加入res
    
import numpy as np
np.argmax(res) #返回最大的后验概率对应的类别

多项式朴素贝叶斯：

当特征是离散变量时，使用多项式模型

高斯朴素贝叶斯：

当特征是连续变量时，使用高斯模型

伯努利朴素贝叶斯：

伯努利模型和多项式模型是一致的，但要求特征是二值化的（1，0）

注意：当特征中既有连续变量又有离散变量时，一般将连续变量离散化后使用多项式模型

•在机器学习中，朴素贝叶斯分类器是一系列以假设特征之间强独立（朴素）下运用贝叶斯定理为基础的简单概率分类器。

•高度可扩展的，求解过程只需花费线性时间

•目前来说，朴素贝叶斯在文本分类（textclassification）的领域的应用多，无论是sklearn还是Spark Mllib中，都只定制化地实现了在文本分类领域的算法