三流Mayavi操作-Mayav-2.1.0.5-points3d,quiver3d绘制

秉着边学边写边折腾的原则，开始粗糙的工作。真正掌握还是得讲解给别人听。 先给出网课
https://www.icourse163.org/course/BIT-1001871001
Mayavi官方
http://docs.enthought.com/mayavi/mayavi/genindex.html
（有时候这网站会装死，一般过几个小时就会活过来）
我发现了，光是三流操作还不够，还得加上四流翻译。

我把目录从这里剔除出去了，否则每次改很麻烦。
这周因为要做一个图示，所以就先把quiver提上来说一下
points3d,quiver3d
单从这两个函数名大概对这两个是比较清楚的，分别绘制的是点和向量。
这两个放在一起也是因为他们的相似参数很多，因为它们都是对点的描述。
这两个而言，是非常有用的两个函数，我比较常用的就是quiver3d因为要绘制向量信息等，这玩意貌似是可以来绘制风场流场的，流体力学是有相当多的应用的。
另外一个points3d的操作很灵活，分析实例的时候有空再说。

1.quiver3d

老规矩从官方例子开始，先微调一下官方代码

import numpy as np
from mayavi.mlab import *
x, y, z = np.mgrid[-2:3, -2:3, -2:3]
r = np.sqrt(x ** 2 + y ** 2 + z ** 4)
u = y * np.sin(r) / (r + 0.001)
v = -x * np.sin(r) / (r + 0.001)
w = np.zeros_like(z)
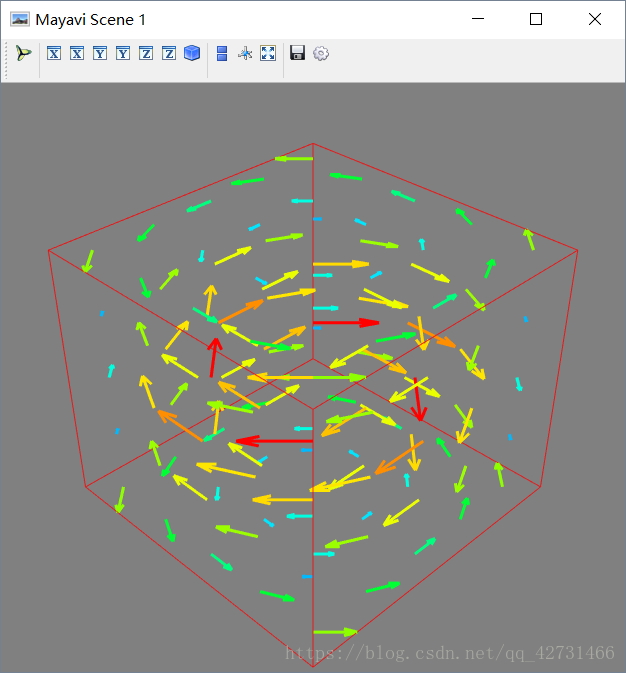
obj = quiver3d(x, y, z, u, v, w, line_width=3, scale_factor=1)
outline(color=(1,0,0),opacity=0.8)
show()

文档中对这个函数的描述如下：
Plots glyphs (like arrows) indicating the direction of the vectors at the positions supplied.
在所给位置放置图形（比如箭头）来表示该处向量的方向。

语法如下：
quiver3d(u, v, w, ...)
quiver3d(x, y, z, u, v, w, ...)
quiver3d(x, y, z, f, ...)

u, v, w are numpy arrays giving the components of the vectors.
If only 3 arrays, u, v, and w are passed, they must be 3D arrays, and the positions of the arrows are assumed to be the indices of the corresponding points in the (u, v, w) arrays.
If 6 arrays, (x, y, z, u, v, w) are passed, the 3 first arrays give the position of the arrows, and the 3 last the components. They can be of any shape.
If 4 positional arguments, (x, y, z, f) are passed, the last one must be a callable, f, that returns vectors components (u, v, w) given the positions (x, y, z).
.
u,v,w由numpy数组给定。
如果只给定(u, v, w),它们必须是一个3D array，且向量箭头的位置假定和(u,v,w)相匹配。
如果(x, y, z, u, v, w)，6个参数被给定，那么前3个arrays给定箭头所在的位置，后三个给定向量，它们的形状可以是任意的。
如果是 (x, y, z, f)的形式，最后一个必须有返回值，(u, v, w)由f返回。

以下开始举例

1.(u, v, w)

代码如下
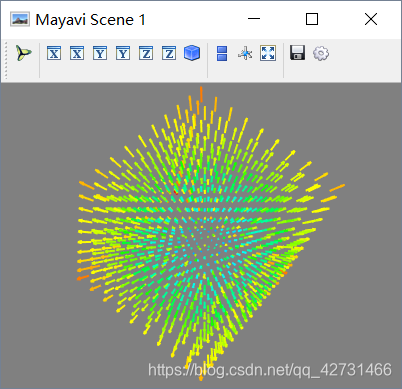
x,y,z = np.mgrid[-5:5,-5:5,-5:5]
mlab.quiver3d(x, y, z)
mlab.show()

2.(x, y, z, f)

.

代码如下：

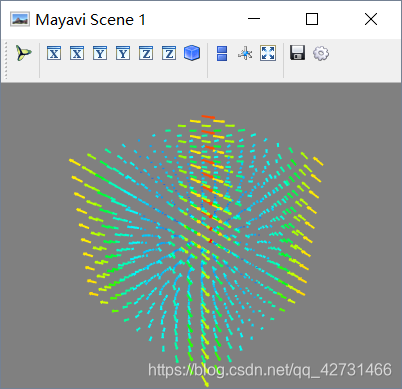
def Shift(x,y,z):
    u = x
    v = x*y
    w = z-1
    return u,v,w
x,y,z = np.mgrid[-5:5,-5:5,-5:5]
mlab.quiver3d(x, y, z,labf)
mlab.show()

也就是多了一了一个f
最后一种就是传入 quiver3d(x, y, z, u, v, w, ...)的形式，不再举例了。
另一例子里面用的是quiver3d(list_x,list_y,list_z,vect_x,vect_y,vect_z,scale_factor=.1)传递的是6个量，这个无所谓的，和这里的方式是一样的~牵涉很多修饰参数，所以看起来率复杂一点。
例子参考：
https://blog.youkuaiyun.com/qq_42731466/article/details/83310151

2.points3d

官方实例微调之后如下。

import numpy as np
from mayavi import mlab
def test_points3d():
    t = np.linspace(0, 4 * np.pi, 20)
    x = np.sin(2 * t)
    y = np.cos(t)
    z = np.cos(2 * t)
    s = 2 + np.sin(t)
    return mlab.points3d(x, y, z, s, colormap="copper", scale_factor=.25)
test_points3d()
mlab.show()

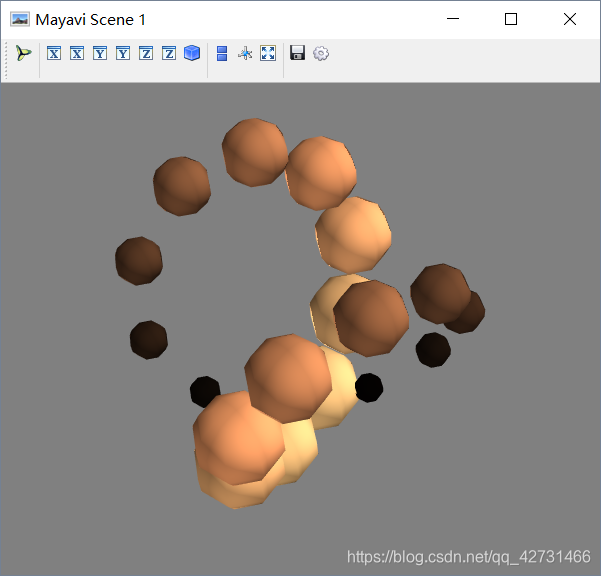
改写一下，其实更清晰一些，但是我什么都没做。后面我用这个说明

import numpy as np
from mayavi import mlab

t = np.linspace(0, 4 * np.pi, 20)
x,y,z = np.sin(2 * t),np.cos(t),np.cos(2 * t)
s = 2 + np.sin(t)

mlab.points3d(x, y, z, s, colormap="copper", scale_factor=.25)
mlab.show()

Plots glyphs (like points) at the position of the supplied data.
在所给位置放置一个图形（点）。
.
语法如下

points3d(x, y, z...)
points3d(x, y, z, s, ...)
points3d(x, y, z, f, ...)

x, y and z are numpy arrays, or lists, all of the same shape, giving the positions of the points.
If only 3 arrays x, y, z are given, all the points are drawn with the same size and color.
In addition, you can pass a fourth array s of the same shape as x, y, and z giving an associated scalar value for each point, or a function f(x, y, z) returning the scalar value. This scalar value can be used to modulate the color and the size of the points.
.
x,y,z为numpy array或者list,他们必须具有相同的维度来表示所要绘制的点的位置。
如果给定x,y,z三个维度，所有的点将被绘制成相同的大小和颜色。
除此之外，你可以传入第4个array的s作为参数，它同样和x,y,z保持相同的维度，为每一个点设置标量值，也可以是一个f函数的形式返回x,y,z的标量值，这个标量值可以用来修改每一个点的颜色的和大小。
.
官方实例中
x,y,z = np.sin(2 * t),np.cos(t),np.cos(2 * t)
s = 2 + np.sin(t)
这2句其实都是围绕t = np.linspace(0, 4 * np.pi, 20)，维度是由t控制的，所以肯定不会出错，这里利用了一个参数方程的思想。
然后最后完成绘制和可视
mlab.points3d(x, y, z, s, colormap="copper", scale_factor=.25)
mlab.show()

所以如果画图的话我也建议使用这种方式，而不是官方的实例，如果代码量大了另当别论。总之灵活处理但不丧失良好可读性。

3.参数

points3d,quiver3d这两个参数之间的不同仅仅在于一个scalars，这个scalars是quiver3d具备的。
其实我是很好奇的，因为这个scalars实际上是赋不进去的

t = np.linspace(0, 4 * np.pi, 20)
x,y,z = np.sin(2 * t),np.cos(t),np.cos(2 * t)
s = 2 + np.sin(t)
sca = t-t    #直接变成和t长度相同的0向量
mlab.quiver3d(x,y,z,x,y,z,scalars=t,scale_factor=1,line_width=3.0)
mlab.points3d(x, y, z, s, colormap="copper", scale_factor=.25)
mlab.show()

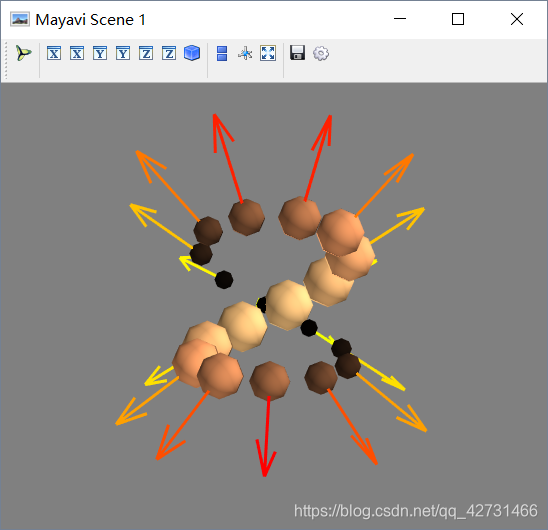
这里标量scalars赋的是0，按理说所有的箭头应具备相同的颜色，但是事实上，一旦 u,v,w一旦给定，那么箭头的长度即确定，且标量也随之确定。所以scalars传入既不会报错也不会有任何改变。

4.补充

暂无
以后减慢更新速度稍微更点想起来的例子玩。

填坑区：

更新
2018.10.20.——因为机器学习的缘故要绘制一个图像，顺带把quiver3d写一点
2018.12.08.——考试繁忙等了很久才更了一下。更完。