PID算法(一)------原理详解

PID简介

  在介绍什么是PID之前先讲述我们需要先明白两个该概念：闭环和开环

开环（Open Loop）：控制器单向输出值给被控对象，不获取被控对象的反馈，控制器对被控对象的执行状态不清楚

闭环（Closed Loop）：控制器输出值给被控对象，同时获取被控对象的反馈，控制器知道被控对象的执行状态，可以根据反馈修改输出值以优化控制

总结：简单来说，开环不需要关注被控对象的状态，闭环需要获取被控对象的状态，根据被控状态的反馈值来修正实际输出值。也就是说开环不具有误差修正功能，闭环具有误差修正功能。

什么是PID

(一)、PID是比例（Proportional）、积分（Integral）、微分（Differential）的缩写

(二)、PID是一种闭环控制算法，它动态改变施加到被控对象的输出值（Out），使得被控对象某一物理量的实际值（Actual），能够快速、准确、稳定地跟踪到指定的目标值（Target）

(三)、PID是一种基于误差（Error）调控的算法，其中规定：误差=目标值-实际值，PID的任务是使误差始终为0。PID对被控对象模型要求低，无需建模，即使被控对象内部运作规律不明确，PID也能进行调控。

注意：(三)中的画线部分可以这么理解

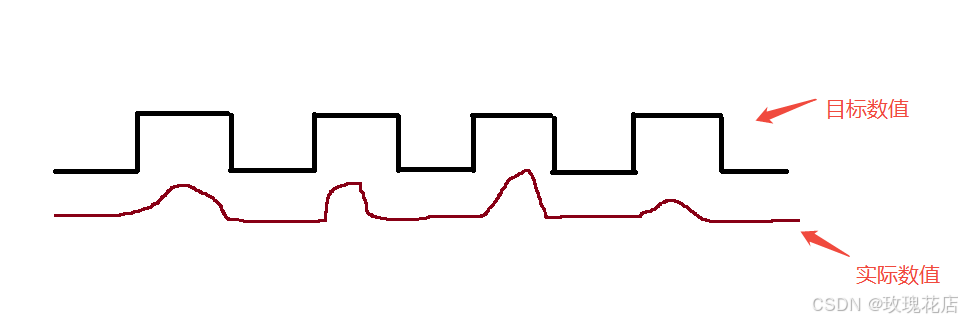
如上图可以看到每个波峰的实际数值和目标数值的误差都不一样，即误差量是不规律的。这种情况PID依然可以进行调控，使得实际曲线尽量体合目标曲线，这就是上面所说的。即使被控对象内部运作规律不明确，PID也能进行调控。

PID公式

$$\begin{array}{rl}①定义误差：error(t)& =target(t)-actual(t)\\ ②PID输出值：out(t)& =K_p(error(t)+\frac{1}{T_i}{\int }_0^{t}error(t)dt+\frac{T_{d}derror(t)}{dt})\\ ③PID输出值：out(t)& =K_p\ast error(t)+K_i\ast {\int }_0^{t}error(t)dt+K_d\ast \frac{derror(t)}{dt}\end{array}$$

上诉公式中可以看出，公式②和③是一样的，公式③中用$K_i$代替$\frac{1}{T_i}$，$K_d$代替了$T_d$。(后续就用公式③来讲述)

注意：PID并不是类似一个由客观事实来推理得到的，而是由经验来构成的。

PID分析

根据上面公式③，我们可以将PID拆成三部分为：

P部分 ： 比例增益，其中$K_p$为比例系数$K_p\ast error(t)$

I部分 ： 积分增益，其中$K_i$为积分系数$K_i\ast {\int }_0^{t}error(t)dt$。

D部分 ： 微分增益，其中$K_d$为微分系数$K_d\ast \frac{derror(t)}{dt}$。

下面我们将对PID三个部分拆解分析，将以PWM驱动电机为实验例子，电机的实际速度和期望速度变化来讲解。下文所表述的$out(t)$可理解为向电机输出的力(实际是改变PWM占空比例影响电机输出的力从而改变电机的转速)。

P部分

只含有比例项的PID输出值：$out(t)=K_p\ast error(t)$

p1、比例项的输出值仅取决于当前时刻的误差，与历史时刻无关。当前存在误差时，比例项输出一个与误差呈正比的值，当前不存在误差时，比例项输出0

p2、$K_p$越大，比例项权重越大，系统响应越快，但超调也会随之增加

p3、纯比例项控制时，系统一般会存在稳态误差，$K_p$越大，稳态误差越小

为了防止陷入误区，这里先讲解一下牛顿三定律

牛顿第一定律：任何一个物体在不受外力或受平衡力的作用（合外力为零）时，总是保持静止状态或匀速直线运动状态，直到有作用在它上面的外力迫使它改变这种状态为止。

牛顿第二定律：物体的加速度跟物体所受的合外力成正比，跟物体的质量成反比，加速度的方向跟合外力的方向相同。即F = ma

牛顿第三定律：两个物体之间的作用力和反作用力，总是同时在同一条直线上，大小相等，方向相反。

那么功率恒定的电机(直流电机)为什么不是一直加速，而是达到最大速度后匀速呢？(不考虑摩擦和电机负载)

1、电机在启动时，由于电流较大，产生的电磁力也很大，导致转子加速。

2、随着转速增加，反电动势逐渐增大，限制了电流的大小。反电动势的增大使得电流逐渐减少，从而减少了电磁力。

3、当反电动势和供电电压达到一定平衡时，电流会趋于稳定，电机的转速也就会稳定下来，进入匀速运行状态。
电机的匀速状态是在电磁力与负载、反电动势之间的平衡下产生的。

下面我们看个公式$P(功率) = U* I $

假设一个电机为的功率为Pw,当启动电机后，电机里面的磁场发生改变，转子切割磁场(磁场方向发生改变导致的切割)产生洛伦磁力
$$F_L=I\ast L\ast B$$

其中 I 是通过电枢导线的电流，L 是导线的有效长度，B 是磁场强度。
因是直流电机所以B是不变化的，L肯定也不变嘛。

U是外部电源电压是不变的，在启动瞬间，I = U/R。$F_s=I_s\ast L\ast B$

由牛二定律可的$a_s=F_s/m$,有了加速度就有了速度，当有了速度以后，此时不单单是磁场方向发生改变导致的切割，由于转子的转动也会主动切割磁感线，则会产生一个反向的电压即反电动势。
$$E_b=k\cdot \omega$$
k是与电机设计和物理特性有关的常数，w是角速度。
则实际电压就为 $U_l=U-E_b$，带入上式可得
$$a=((U-E_b)/R\ast L\ast B)/m$$

则容知，是随着转速的增加，加速度w也会增大，反动电势增大。则加速度a会减小($V=V_0+a_i\ast t$)注意加速度虽然在减小，速度还是在增加的哈，当反动电势和电源电压相互抵消后，加速度为0,此时速度达到最大值。也可知在启动瞬间实际功率是远大于额定功率Pw的，当速度稳定后功率稳定为Pw，此时的功率也叫额定功率。

了解上诉部分再来看p1、p2、p3。

p1项很容易理解$out(t)=K_p\ast error(t)$，$error(t)$为0，out肯定为0麻。
p2项目，在电机启动瞬间，目标数值和实际数值差值肯定是最大的嘛，输出的力也是最大的，所以转速变化是最快的，系统响应是最快的。如下图启动时刻那个尖尖(启动瞬间过后，有了速度error(t)减小，所以out(t)也减小，所以会下降)。当速度n满足out(t) = 反电动势 + 摩擦力，此时系统稳定。超调可以看0-100,和100-0的瞬间，此时error(t)变化最大，因此变化最激烈，所以Kp越大，超调越严重。如果我们的期望目标不变，Kp越大则稳定后的曲线越靠近目标曲线，因此Kp越大稳态误差越小。

$K_p=0.25$

$K_p=0.5$

P+I部分

你可能会说，我当前的误差量+ 上次次输出的值，不应该是这样做吗？是的没错，这个做法正是P+I项。

我们先看一下I项的特点

I1、积分项的输出值取决于所有时刻误差的积分，与历史时刻有关。积分项将历史所有时刻的误差累积，乘上积分项系数后作为积分项输出值。

I2、积分项用于弥补纯比例项产生的稳态误差，若系统持续产生误差，则积分项会不断累积误差，直到控制器产生动作，让稳态误差消失

I3、积分项权重越大，稳态误差消失越快，但系统滞后性也会随之增加

直白点解释，I项目就是对历史误差的积分，举个例子，$K_i\ast {\int }_0^{t}error(t)dt$，假设Ki = 0.2；目标值是100,第一时刻误差是100 -0 = 100，则第二时刻的数值是20,第二时刻的误差是80,则第三时刻为20+80*0.2 = 36…以此类推直到没有误差。其曲线入下图：

误差越来越小，因此积分数值的变化率越来越小。

即分享I1、I2、I3都很好理解，但是注意这一句但系统滞后性也会随之增加,Ki越大，应该响应越快，为什么反而会滞后呢？
假设我们的Ki = 10;需要把转速由0变化到100,第一时刻历史误差为0,因此不变，第二时刻历史误差为100,100*10=1000,严重超调，是不是需要反过来调节，这不是也花费时间吗，越大花费的时间越久麻，过大严重过大甚至无法调节到稳态，形成严重的系统振荡。

结合下图PI的调控来看就比较好理解了

P+I+D部分

在上述讲述中易知，当Kp过大容易造成瞬间急剧变化，如果在加上Ki项的助力，这种变化更加剧烈。为避免这种情况因此我们引入了D项，即微分项。

$$K_d\ast \frac{derror(t)}{dt}$$

D1、微分项的输出值取决于当前时刻误差变化的斜率，与当前时刻附近误差变化的趋势有关。当误差急剧变化时，微分项会负反馈输出相反的作用力，阻碍误差急剧变化

D2、斜率一定程度上反映了误差未来的变化趋势，这使得微分项具有 “预测未来，提前调控”的特性

D3、微分项给系统增加阻尼，可以有效防止系统超调，尤其是惯性比较大的系统
K_d越大，微分项权重越大，系统阻尼越大，但系统卡顿现象也会随之增加

对于这个公式简单点理解，就是当前时刻的斜率。

我们看一组示意图

可以看到越来越接近目标值，且变化的增量越来越快(斜率越来越大)。
再看看误差和时间的变化

可以看到误差的斜率也是越来越大，但是误差的斜率是负数，所以Kd越大阻尼越大。