堆排序

堆排序

这次小编来分享一下自己对于堆排序的归纳与总结，在介绍堆排序之前，我希望大家知道堆排序除了具备更高的效率以外，在查找最大值，第几个最大值，最小值，第几个最小值时有着极大的便利性

堆

1）堆的定义

  堆是一种数据结构，堆结构就像生活中的叠罗汉，只不过叠的对象不再是人而是数字。那么计算机中的叠罗汉是什么形式呢？没错，正是完全二叉树的形式，我们需要注意的是堆是用数组实现的完全二叉树，所有它并没有使用父指针或者子指针

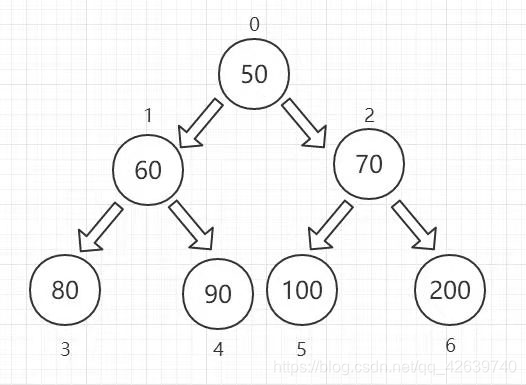
2）堆结构的特点

① 大顶堆：每个结点的值都大于或等于其左右孩子结点的值

 
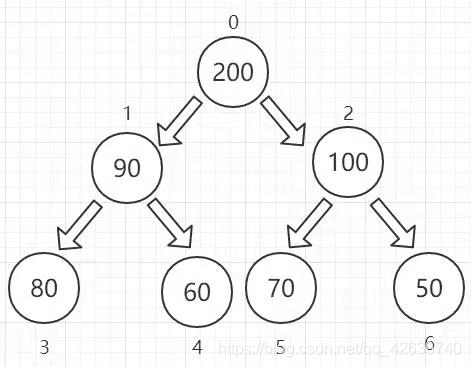
② 小顶堆：每个结点的值都小于或等于其左右孩子结点的值

 
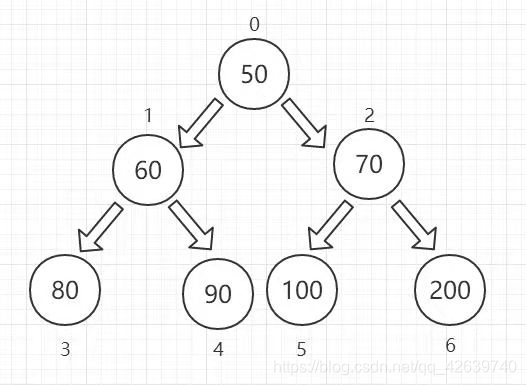
③ 数组下标与左右孩子结点的关系

根结点下标	左孩子结点下标	右孩子结点下标
i	2*i+1	2*i+2
0	1	2
1	3	4
2	5	6

至此我们已经成功的将堆与待排数组相联系

堆排序的特点

  小编在之前写过的简单排序中，选择排序通过减少交换次数得到了一定程度上的优化，但是在每次的不可避免的比较过程中，选择排序无法将每趟比较的结果记录下来，这将导致在之后的比较中会出现较多次的重复工作

  堆排序实际上是一种对选择排序的改进，它实现了在每次选择的过程中对数据进行相应的调整，使得在排序的总体过程中大大的减少了重复工作的次数

堆排序的原理

小编所举例子是通过构建大顶堆获得有序序列

1）原理简述

  堆排序将待排序的n个元素构造成一个大顶堆，此时元素中的最大值便在堆顶的根结点（下标为0）。将它与末尾元素交换使得最大元素排在末尾，然后将剩余的n-1个元素重复上述操作，最终得到排序结果

2）原理图

  在进行图解说明之前，我们不妨思考一个重要的问题：如何保证根结点的元素为整棵完全二叉树中的最值？我们的比较次序应该是由上至下，还是由下至上？相信大家都已经想明白了，自然是由下至上，只有这样才能真正得到堆顶元素，其实这就像我们竞选校级干部，先要让同学们选出几个优秀的候选人，接着是老师选，最后才是校长作出最终决定

  我们以数组arr[7]={50,80,70,100,90,20,200}为例

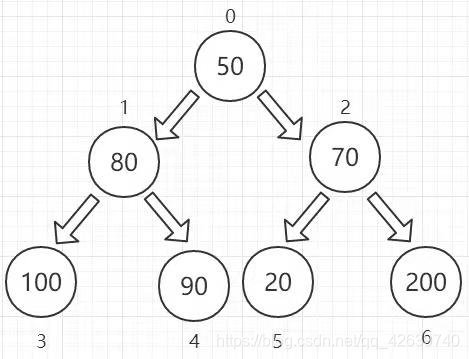
根据我们之前的分析，我们的比较应该由下至上，所以我们首先应该先得到结点1上的最值与结点2上的最值，只有这样才通过最终比较（0,1,2）获得根结点上的最值

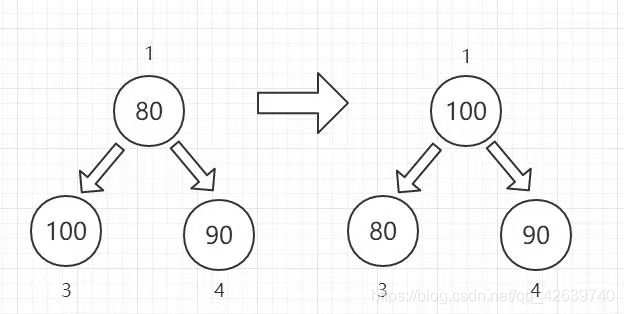
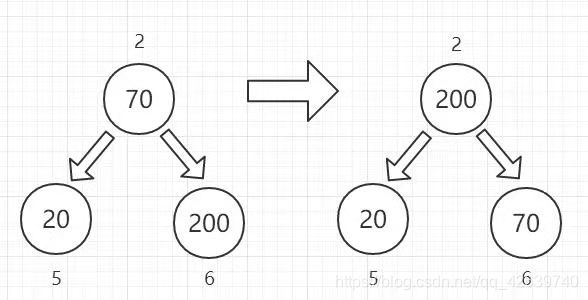
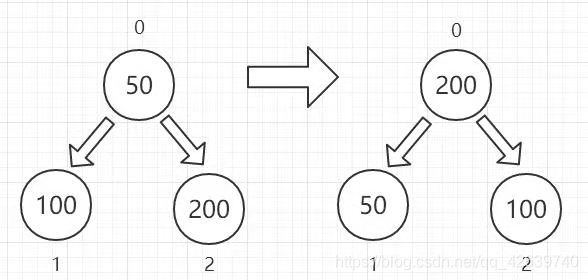
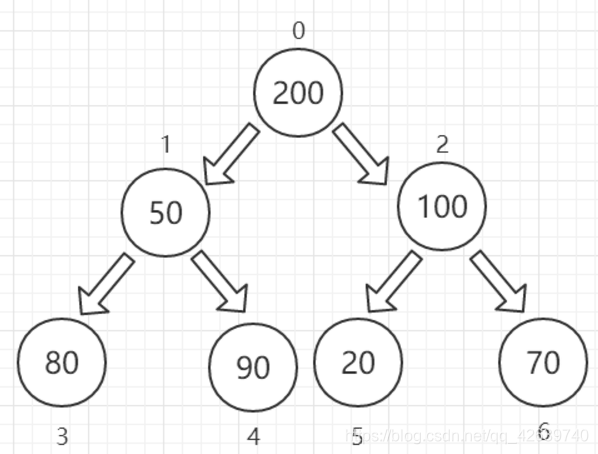
至此我们在第一次循环中便得到了大顶堆，接下来只需进行交换操作即可

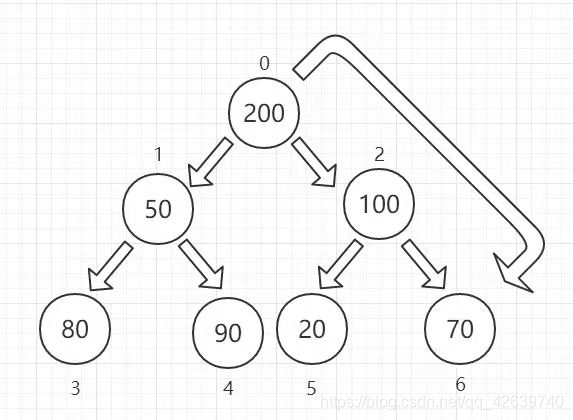
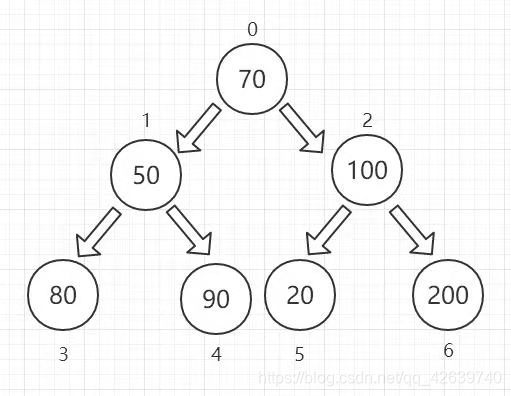
至此我们完成了交换操作，那么下一次我们所排序的堆应该是怎么样的呢？

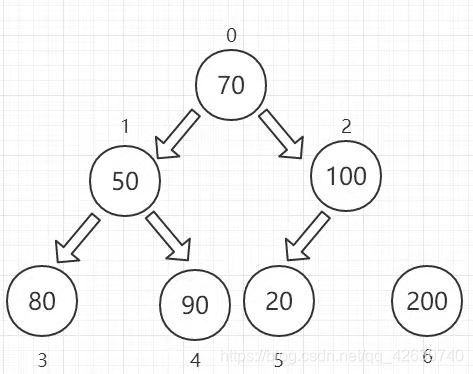
此时我们不在比较结点6，因为它已经是我们找到的最大值了，接下来的工作便是循环得到次大值

实现代码

//宏定义实现交换函数
#define swap(a,b) {typeof(a) t=a;a=b;b=t;}

//创建大顶堆
void create_heap(int* arr,size_t root,size_t len)
{
	if(root >= len) return;       //当根结点下标超过数组长度时结束递归
	int left = 2*root+1;          //当前根结点的左孩子结点
	int right = 2*root+2;         //当前根结点的右孩子结点

	//为了实现由下至上的比较顺序
	create_heap(arr,left,len);    //一直往左遍历
	create_heap(arr,right,len);   //一直往右遍历

	int max = root;
	if(left<len)
	{
        if(arr[left] > arr[max])
           max = left;
	}
	if(right<len)
	{
        if(arr[right] > arr[max])
           max = right;
	}
	if(root != max)
	{
        swap(arr[max],arr[root]);
	}
}

//堆排序
void head_swap(int* arr,size_t len)
{
	for(int i=0;i<len;++i)
	{
        create_heap(arr,0,len-i);
        swap[arr[0],arr[len-i-1]];
	}
}

总结

  以上是小编对堆排序的归纳，小编认为其实堆排序的遍历过程与二叉树的遍历过程十分相像，只不过多了最后的比较过程，希望大家能通过图解理解代码的具体含义，若有不全之处请及时指出，望大佬们海涵