数据挖掘十大算法(五)：SVM算法

前言

SVM的英文全称是Support Vector Machines，我们叫它支持向量机。支持向量机是我们用于分类的一种算法。
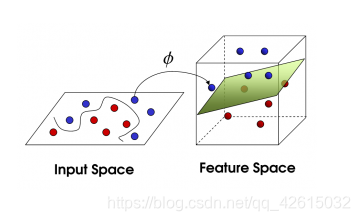
当一个分类问题，数据是线性可分的，也就是用一根棍就可以将两种小球分开的时候，我们只要将棍的位置放在让小球距离棍的距离最大化的位置即可，寻找这个最大间隔的过程，就叫做最优化。但是，现实往往是很残酷的，一般的数据是线性不可分的，也就是找不到一个棍将两种小球很好的分类。这个时候，我们就需要像大侠一样，将小球拍起，用一张纸代替小棍将小球进行分类。想要让数据飞起，我们需要的东西就是核函数(kernel)，用于切分小球的纸，就是超平面。


理解一个SVM独有的概念”分类间隔”。
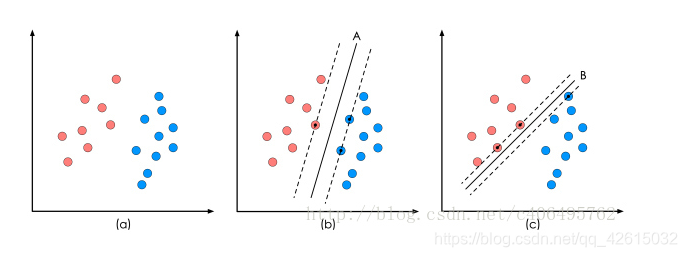
在保证决策面方向不变且不会出现错分样本的情况下移动决策面，会在原来的决策面两侧找到两个极限位置（越过该位置就会产生错分现象），如虚线所示。虚线的位置由决策面的方向和距离原决策面最近的几个样本的位置决定。而这两条平行虚线正中间的分界线就是在保持当前决策面方向不变的前提下的最优决策面。两条虚线之间的垂直距离就是这个最优决策面对应的分类间隔。
显然每一个可能把数据集正确分开的方向都有一个最优决策面（有些方向无论如何移动决策面的位置也不可能将两类样本完全分开），而不同方向的最优决策面的分类间隔通常是不同的，那个具有“最大间隔”的决策面就是SVM要寻找的最优解。而这个真正的最优解对应的两侧虚线所穿过的样本点，就是SVM中的支持样本点，称为”支持向量”。

一、数学建模

基本数学推导

一个最优化问题通常有两个基本的因素：1）目标函数，也就是你希望什么东西的什么指标达到最好；2）优化对象，你期望通过改变哪些因素来使你的目标函数达到最优。
具体数学建模过程请见：https://blog.youkuaiyun.com/c406495762/article/details/78072313 写的非常好！

得到超平面方程：

支持向量到超平面的距离的计算方式：

我们目的是为了找出一个分类效果好的超平面作为分类器。分类器的好坏的评定依据是分类间隔W=2d的大小，即分类间隔W越大，我们认为这个超平面的分类效果越好。此时，求解超平面的问题就变成了求解分类间隔W最大化的问题。W的最大化也就是d最大化。

那么就存在两个问题：
我们如何判断超平面是否将样本点正确分类？
怎么在众多的点中选出支持向量上的点呢？

引入约束条件：

线性SVM优化问题基本描述

提示：当我们只考虑支持向量上的点的时候，d的分子是固定的 等于1.

以上是SVM的基本数学模型 更加深层的算法不再介绍

引入黑科技-核函数

上面说的都是在原始特征的维度上，能直接找到一条分离超平面将数据完美的分成两类的情况。但如果找不到呢？

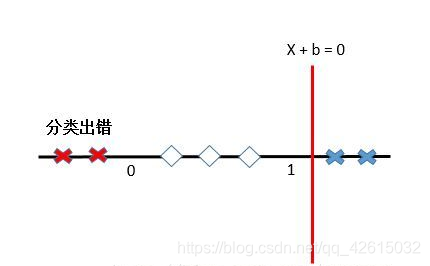
比如，原始的输入向量是一维的，0< x <1的类别是1，其他情况记做-1。这样的情况是不可能在1维空间中找到分离超平面的（一维空间中的分离超平面是一个点，aX+b=0）。你用一个点切一下试试？

这就要说到SVM的黑科技—核函数技巧。核函数可以将原始特征映射到另一个高维特征空间中，解决原始空间的线性不可分问题。

继续刚才那个数轴：

如果我们将原始的一维特征空间映射到二维特征空间X^{{2}和x，那么就可以找到分离超平面X}{2}-X=0。当X^{{2}-X<0的时候，就可以判别为类别1，当X}{2}-X>0 的时候，就可以判别为类别0。如下图：

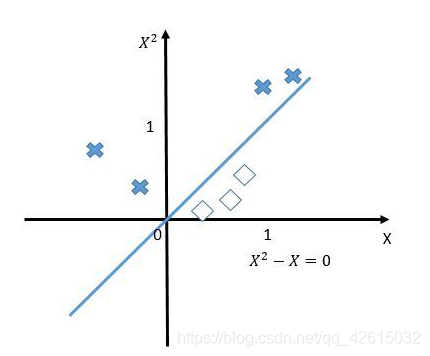
再将X^2-X=0映射回原始的特征空间，就可以知道在0和1之间的实例类别是1，剩下空间上（小于0和大于1）的实例类别都是0啦。

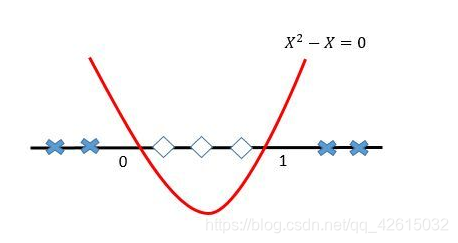
利用特征映射，就可以将低维空间中的线性不可分问题解决了。核函数除了能够完成特征映射，而且还能把特征映射之后的内积结果直接返回，大幅度降低了简化了工作，这就是为啥采用核函数的原因。

二、实战

SVM有三种模型，由简至繁为
当训练数据训练可分时，通过硬间隔最大化，可学习到硬间隔支持向量机，又叫线性可分支持向量机
当训练数据训练近似可分时，通过软间隔最大化，可学习到软间隔支持向量机，又叫线性支持向量机
当训练数据训练不可分时，通过软间隔最大化及核技巧(kernel trick)，可学习到非线性支持向量机

sklearn.svm参数

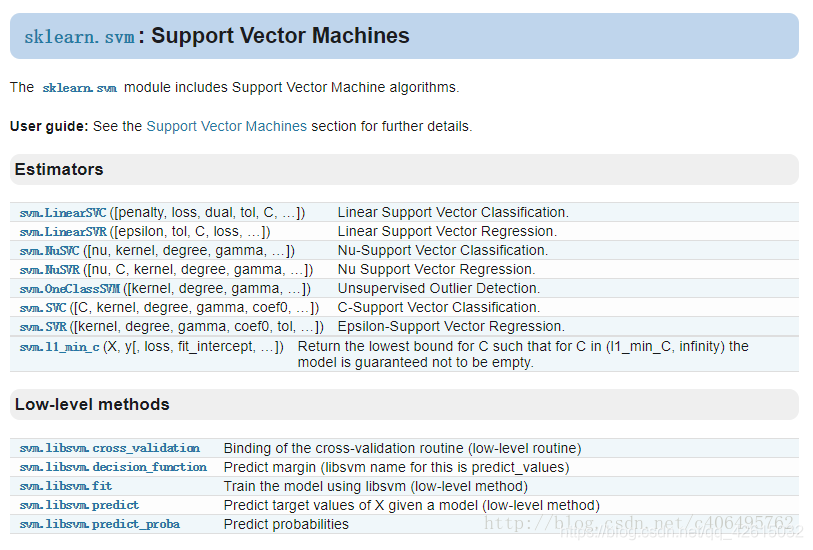
SVC很是强大，我们不用理解算法实现的具体细节，不用理解算法的优化方法。同时，它也满足我们的多分类需求。

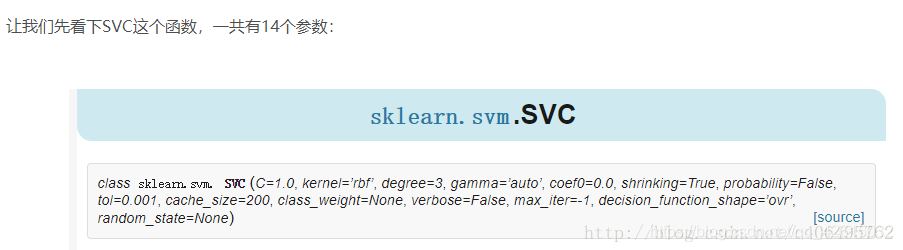
C：惩罚项，float类型，可选参数，默认为1.0，C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低，也就是对测试数据的分类准确率降低。相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。

kernel：核函数类型，str类型，默认为’rbf’。

gamma：核函数系数，float类型，可选参数，默认为auto。只对’rbf’ ,’poly’ ,’sigmo