【集成学习系列教程6】随机森林Random Forest原理及sklearn应用

原创已于 2022-08-22 22:33:07 修改 · 1.7k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #集成学习

于 2021-09-30 15:39:29 首次发布

集成学习专栏收录该内容

6 篇文章

订阅专栏

本文探讨了随机森林算法的参数调优，包括max_features、n_estimators、max_depth等，通过实例分析了otto数据集的分类问题，展示了如何利用包外误差曲线评估模型性能。关键步骤包括自助采样、特征选择、模型训练与评估。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

8 Bagging基本思想及工作过程

前面我们介绍了集成学习中的一大类算法——Boosting算法，它利用基学习器之间的相关性，通过串行地生成多个新的基学习器，获得最终的强学习器，是一种非常具有代表性的“串行集成方法”。而集成学习方法中还有另一大类算法——Bagging算法，它利用的是基学习器之间的独立性，通过结合多个相互独立的基学习器，从整体上显著减小拟合的误差，是一种非常具有代表性的“并行集成方法”。本节就将对Bagging方法进行详细的介绍。

Bagging的全称为Bootstrap Aggregating，包含bootstrap(自助)和aggregating(聚合)两大含义。

8.1 自助

所谓“自助”，指的是Bagging中采用了自助采样方法。在上一章我们介绍GBDT时提到了subsample（子采样）方法，它在训练每个基学习器时不是使用所有的训练样本，而是只随机采样其中的一部分来训练。而自主采样方法与子采样方法有点类似，也是每次只取训练数据集中的一部分来训练基学习器，但子采样方法用的是无放回抽样的方法，而自助采样方法采用的是有放回抽样的方法。这里举一个具体一点的例子来介绍该方法。

假设有一个样本数为 $m$ 的训练数据集 $D$ ，我们采用如下方法形成一个新的数据集 $D^{'}$ ：

创建一个空的数据集 $D^{'}$ ；
每次从 $D$ 中随机挑选一个样本 $\boldsymbol x_i$ ，将其进行复制得到另一个完全一样的样本 $\boldsymbol x_i^{'}$ ，然后将 $\boldsymbol x_i^{'}$ 放入 $D^{'}$ 中，再将 $\boldsymbol x_i$ 放回 $D$ ；
重复执行 $m$ 次上述步骤，得到一个新数据集的 $D^{'}$ ，并将 $D^{'}$ 用于其中一个基学习器的训练；
重复执行 $T$ 次上述步骤，得到 $T$ 个样本分布差异较大的新数据集 $D^{'}_t(t=1,2,...,T)$ ，并将 $D^{'}_i$ 用于 $T$ 个基学习器的训练，从而得到 $T$ 个差异较大的基学习器。

从上面的步骤可以推断， $D$ 中会有一部分样本在 $D^{'}$ 中反复出现，但由于每次只取出一个样本，用完就放回去，所以同时也有一部分样本永远不会出现在 $D^{'}$ 中。由于每次抽取中样本被抽到的概率是 $1/ m$ ，每次抽取中样本没有被抽到的概率就是 $(1 - 1/ m)$ ，取了 $m$ 次都没有被抽到的概率就是 $(1-\frac{1}{m})^m$ 。假设 $m$ 非常大，趋向于正无穷，那么我们可以得到如下的公式：
$\lim_{m\rightarrow+∞}(1-\frac{1}{m})^m=\frac{1}{e}≈0.368$
也就是说，我们经过多次自助采样之后，数据集 $D$ 中大约有三分之一的样本从未出现在采样数据集 $D^{'}$ 中。把这部分样本组成的数据集称为 $D^{''}$ ，则 $D^{''}=D-D^{'}$ 。这些新数据集各自的用途为：

$D^{'}$ 作为训练集，用于基学习器的训练；
$D^{''}$ 作为测试集，用于评估基学习器在 $D^{'}$ 上的拟合效果。 $D^{''}$ 中的样本称为包外样本，用 $D^{''}$ 评估基学习器拟合效果的方法称为out-of-bag estimate(包外样本估计，简称oob)。一般我们用基学习器在包外样本上预测误差的均值作为Bagging算法的泛化误差，计算公式为：
$err^{oob}=\frac {1}{|D|}\sum_{(\boldsymbol x,y)\in D}I(h^{oob}(\boldsymbol x) \ne y)$
其中 $h^{oob}(\boldsymbol x)$ 为基学习器 $h(\boldsymbol x)$ 在包外样本 $\boldsymbol x$ 上的预测值。

使用自助采样法可以从原始数据集 $D$ 中分化出丰富多样的新数据集，将这些不同的数据集用于不同基学习器的训练，有助于增大各个基学习器之间的差异性与独立性，这与Bagging方法的思想非常吻合。

8.2 聚合

我们通过自助得到了 $T$ 个差异较大的基学习器，但它们是相互独立的，所以我们还需要将它们的结果给整合成最终强学习器的输出结果。这时就要用到聚合的方法。聚合分为两种情况：

在分类问题中，聚合表示“多数投票”方法。比如，在通过自助采样得到 $T$ 个新数据集 $D^{'}_t$ 、并将 $D^{'}_t$ 分别用于基学习器 $h_t$ 的训练之后，会得到 $T$ 个类别标记预测结果 $c_t$ 。对 $c_t$ 进行统计，得票数最多的类别标记就作为强分类器的最终预测结果输出。如果有多个得票数最多的结果，则随机从中选取一个作为预测结果。这样我们就得到了Bagging算法的目标函数：
$H(\boldsymbol x)=\mathop {\arg\max} _{y\in Y}\sum_{t=1}^TI(h_t(\boldsymbol x)=y)$
在回归问题中，聚合表示“取平均值”的方法，即对多个基学习器的回归预测结果取平均值，作为最终强学习器的输出。

通过自助和聚合这两个步骤，我们就完成了Bagging算法的步骤。

8.3 注意事项

Bagging需要配合不稳定学习器使用，且学习器越不稳定，Bagging算法的预测效果越好。所谓不稳定学习器是指对训练数据集的分布较敏感、预测结果随着训练数据集分布的变化会产生较大差异的学习器。决策树就是典型的不稳定学习器，并且当深度较深时，决策树的预测结果所产生的变数也较大，也较符合Bagging算法的要求。因此，使用未剪枝决策树对Bagging算法的提升作用比剪枝后的决策树对Bagging算法的提升作用大。这也减小了实际使用中用户的调参负担。

9 随机森林

9.1 概述

随机森林算法是一种非常受欢迎的集成学习方法，受到了非常广泛的应用。它巧妙借鉴了Bagging算法的思想，被称为Bagging算法的升级版，但与Bagging算法又有着明显的不同。主要体现在：Bagging算法是在基学习器训练样本的选择上引入了自助采样方法，增加了不同基学习器训练样本的随机性；而随机森林则将Bagging中样本选择的随机性改成了特征选择的随机性。随机森林的主体思想为：

基学习器全部选用决策树，不能是其他类型（随机森林都由树组成，所以才被叫做森林）；
训练基学习器用的是在数据集中随机选择的一个包含 $k$ 个特征的子集；
$k$ 特征子集在每个基学习器上的训练方式与单棵决策树一致，都是在每次分裂时选择一个最佳属性作为划分的依据。

上面 $k$ 的选择方式有很多种，主要分为如下三种情况（下面 $d$ 为样本总的特征数）：

当 $k = d$ 时，基学习器的构建方式与传统决策树相同；
当 $k = 1$ 时，基学习器在所有 $d$ 个特征中随机选择1个特征作为划分的依据；
$k$ 也可以有其他的取值，比较推荐的值为特征数的对数，即 $k=log_2d$ 。

9.2 算法步骤

随机森林算法的步骤如下：

从原始训练集中使用自助采样方法样选出每组 $m$ 个、共进行n_tree次采样，生成n_tree个训练集；
对于n_tree个训练集，我们分别训练n_tree个决策树模型；
对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/基尼系数选择最好的特征以及最好的特征分割阈值进行分裂；
每棵树都一直这样分裂下去，直到该节点的所有训练样例都属于同一类。由于Bagging类算法的特性，在分裂过程中不需要剪枝；
将生成的多棵基决策树组成随机森林。对于分类问题，按多数投票机制确定最终分类结果；对于回归问题，将多棵树预测回归值的均值作为最终预测结果。

这样我们就完成了随机森林算法的步骤。

9.3 sklearn中的随机森林

9.3.1 原型

class sklearn.ensemble.RandomForestClassifier(n_estimators=100,*, criterion='gini', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None, ccp_alpha=0.0, max_samples=None)

9.3.2 参数

sklearn中随机森林的参数可分为两部分：一部分为决策树参数，一部分为特有参数。

决策树的参数

criterion：{“gini”, “entropy”}，默认为 ”gini”

表示决策树中节点分割的指标。”gini”表示基尼不纯度，entropy表示信息增益。
splitter：{”best”, “random”}，默认为 ”best”

表示节点分割的属性依据。"random"表示随机选择属性，”best”表示选择不纯度最大的属性。建议用“best”。
max_features：{“auto”, “sqrt”, “log2”}, 可设置为整数或浮点数，默认为 ”auto”

表示选择最适属性进行划分时所允许的最大特征数。指定为当为整数时，该整数就是分割所允许的最大特征数；指定为小数时，所允许的最大特征数为数据集的总特征数×该小数。不妨设数据集的总特征数为n_features，则自带的各个选项的含义为：
- “auto”：max_features=sqrt(n_features)
- “sqrt”：max_features=sqrt(n_features)
- “log2”：max_features=log2(n_features)
- None：max_features=n_features
max_depth：整型，默认值为 None

表示树的最大深度，默认值None表示建树时会使每一个叶子节点都只有一个类别的样本，或者所有的叶子节点都包含少于min_samples_split个样本。
min_samples_split：整型或浮点型，默认值为 2

表示根据属性划分节点时，每次划分所需要的最少样本数。
min_samples_leaf：整型或浮点型，默认值为 1

表示叶子节点所需要的最少样本数。
max_leaf_nodes：整型或浮点型，默认值为 None

表示叶子节点的最大数量，默认值None表示不进行叶子节点数量的限制。
min_weight_fraction_leaf：浮点型，默认值为 0.0

表示叶子节点所需要的最小权值。
verbose：整型，默认值为0，

表示是否显示任务进程，默认值0表示不显示。

随机森林的特有参数

n_estimators：整型，默认值为100
表示基决策数的数量。
bootstrap：布尔型，默认为True

表示是否使用自助采样方法。
oob_score：布尔型，默认为False

表示是否使用包外数据集来评估模型对数据集的拟合效果。
warm_start：布尔型，默认为False

表示是否启用热启动机制。
class_weight：{“balanced”, “balanced_subsample”}，字典类型或字典列表类型，默认为None

表示各个标签的权值，默认值None表示所有标签的权重均为1。
n_jobs：整型，默认值为None

表示并行运算的CPU数量，指定为-1表示调用所有CPU核进行运算，会快很多。

下面的两个实例将会对这些参数的使用做详细演示。

9.3.3 属性

base_estimator_：返回基决策树的种类、详细参数等信息。
estimators_：返回迭代过程中所有生成的弱学习器的信息。
classes_：所有类别的标签。
n_features_：数据集的特征数。
feature_importances_：返回数据集中每个特征的权重的组成的列表。
oob_score_：当且仅当参数oob_score=True时有用。表示模型在包外样本上的预测准确率。

9.3.4 方法

apply：将随机森林中的决策树应用于数据集 $X$ ，返回叶子节点的索引。
decision_path(X)：获取随即森林模型对样本 $X$ 的决策路径。
fit(X,y,[,sample_weight]：拟合数据集。
get_params([deep])： $d ee p$ 参数指定为 $T r u e$ 时，返回集成分类器的各项参数值。
set_params(**params)：设置参数。
predict(X)：对数据集 $X$ 中各样本进行预测。
predict_proba(X)：计算出样本 $X$ 属于各个类别的概率。
predict_log_proba(X)：返回对数据集 $X$ 中各样本预测结果的自然对数值。
score(X, y[, sample_weight])：返回模型在给定数据集 $X$ 上的平均预测准确率。

9.4 实例6：利用包外误差曲线评估随机森林模型

在前面的原理部分我们介绍了包外样本估计的概念，并且已经知道：使用包外样本估计方法可以非常方便地对基分类器的好坏进行评估。而包外样本估计方法中一个非常重要的评估指标是包外误差(out-of-bag error)，它是指所有基分类器在未被选中的样本集上的平均误差。下面这个示例就演示了我们如何绘制包外误差随基学习器数量（迭代次数）的增加而变化的曲线，以及我们如何通过观察曲线图对比不同模型泛化性能的好坏，并确定合适的迭代次数。

9.4.1 数据集的创建

这里我们使用sklearn中的make_classifier函数来创建一个数据集。该函数的原型如下：
sklearn.datasets.make_classification(n_samples=100, n_features=20, *, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)

常用参数如下：

n_samples:：整型，默认值为100
表示所要创建数据集的样本数。
n_features：整型，默认值为20
表示样本的特征数。这些特征里面可能包含如下多个不同种类的特征，它们同样可以用该函数中自带的参数来量化。
n_informative：整型，默认值为2
表示具有较多信息的、具有代表性的特征的数量。该函数创建的数据集中，每个类别可能具有多个点蔟，而每个样本又可能具有很多个特征，但其中只有一部分特征组合起来形成的子空间满足高斯分布，这部分特征就是最具有代表性的特征，这些特征的总数量就由该参数定义。
n_redundant：整型，默认值为2
表示冗余特征的数量。
n_repeated：整型，默认值为0
表示重复特征的数量。
以上4个指定特征数的参数中最常用的是n_features和n_informative，其他两个不怎么常用。
n_classes：整型，默认值为2
表示数据集总的类别数.
n_clusters_per_class：整型，默认值为2
表示同一类样本中的点蔟数。该值越大，表示同一类样本的点蔟数越多，数据集的非线性特征越强，对模型非线性表达能力的要求也越高。
random_state：整型，默认为None
表示随机数种子，将该值设为一个常熟可以保证每次运行创建的数据集均相同，便于代码复用。

为了便于评估随机森林模型的性能，这里选择创建一个相对不那么复杂的数据集。代码如下：

X, y = make_classification(n_samples=1000, n_features=40, n_clusters_per_class=1, n_informative=20,  random_state=3333)

9.4.2 模型的创建与拟合

我们将从如下几个方面对比不同随机森林模型的好坏：

其他参数相同，改变max_feature的值，观察对比不同max_features取值下随机森林模型分类效果的好坏（以oob错误率为指标），并找出最佳模型；
观察最佳模型曲线的走势，确定较合适的迭代次数。

为了探究不同max_feature取值（即用于基学习器分裂的特征子集的特征数）下随机森林的拟合效果随迭代次数增加的变化情况，我们选择定义下面三个模型中，这些模型在定义时都指定了参数warm_start=True，表示启用热启动机制。因为我们在后面会在一个循环体中通过RandomForestClassifier中的set_params函数不断改变模型的n_estimators参数，而其他参数保持不变。在只改变一个参数的值的情况下，不断训练全新的模型是非常浪费计算资源的，所以这里通过启用热启动机制，使得新模型可以充分利用之前训练得到的模型状态，再在此基础上进行参数的调整，这样可以大幅节省计算资源，耗时也更少。代码如下：

# 定义模型列表
rf_clfs_with_dif_max_depth = [
    # 定义max_features=sqrt(n_features)的模型
    ("RandomForestClassifier, max_features='sqrt'",
        RandomForestClassifier(warm_start=True, oob_score=True,
                               max_features="sqrt",
                               random_state=123,
                              n_estimators=10)),
    # 定义max_features=log2(n_features)的模型
    ("RandomForestClassifier, max_features='log2'",
        RandomForestClassifier(warm_start=True, max_features='log2',
                               oob_score=True,
                               random_state=123,
                              n_estimators=10)),
    # 定义max_features=n_features的模型
    ("RandomForestClassifier, max_features=None",
        RandomForestClassifier(warm_start=True, max_features=None,
                               oob_score=True,
                               random_state=123,
                              n_estimators=10))
]

9.4.3 oob错误率曲线的绘制

代码如下：

# 构建起迭代次数n_estimators和oob错误率的映射关系的列表
error_rate = OrderedDict((label, []) for label, clf in rf_clfs_with_dif_max_depth)

# 定义要探索的最小迭代次数和最大迭代次数
min_estimators = 10
max_estimators = 500
index = 0
max_sample_list = ['sqrt(n_features)', 'log2(n_features)', 'n_features']
for label, clf in rf_clfs_with_dif_max_depth:
    # 定义迭代次数的范围为(10, 500)，步长为10
    for i in np.arange(min_estimators, max_estimators+10, 10):
        # 更新模型的迭代次数
        clf.set_params(n_estimators=i)
        # 使用更新后的模型对数据集进行拟合，并在经过所有500轮迭代之后记录下不同模型拟合的时间
        t1 = time.time()
        clf.fit(X, y)
        t2 = time.time()
        if(i == 500):
            print("Total fitting time of random forest model with max_depth=%s is %.4fs" % (max_sample_list[index], t2-t1))
            index +=1      
        # 求出每次模型更新后的oob错误率，并将当前模型的迭代次数n_estimators和oob错误率的映射关系加入error_rate列表当中。
        oob_error = 1 - clf.oob_score_
        error_rate[label].append((i, oob_error))

plt.figure(figsize=(10, 6))       
for label, clf_err in error_rate.items():
    # 以映射列表error_rate中的n_estimators作为横轴，oob错误率作为纵轴，画出曲线图
    xs, ys = zip(*clf_err)
    plt.plot(xs, ys, label=label)
    color_index += 1

plt.xlim(min_estimators, max_estimators)
plt.xlabel("n_estimators")
plt.ylabel("oob error rate")
plt.legend(loc="upper right")

输出结果如下：

Total fitting time of random forest model with max_depth=sqrt(n_features) is 0.4779s

Total fitting time of random forest model with max_depth=log2(n_features) is 0.3951s

Total fitting time of random forest model with max_depth=n_features is 0.6383s

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FeVH1SVG-1632986952062)(oob_error_curve.png)]

上述输出结果中包含拟合时间和曲线图两大部分。先来对比不同模型的拟合时间，可以看到，当模型的max_features参数指定为log2时，模型对数据集的拟合时间最少。观察曲线图，可以看到：虽然max_features='log2’时用于模型分裂可选择的特征数较少，但是其对应的oob错误率曲线在大约第300轮迭代之后收敛到三个模型中的最低水平。而当max_features=None（即max_features=总特征数）时，虽然曲线的收敛速度最快，但最终收敛达到的oob错误率却最高。综上分析：指定max_features='log2’时，随机森林模型的拟合效果最好，而这也是公认较常用、效果较好的max_features参数的取值。读者可以参考上述方法，并尝试用到随机森林分类模型其他参数的优化当中。

9.5 实例7：用随机森林解决otto数据集分类问题

本实例将使用随机森林解决一个实际的机器学习问题，一来是为了给读者提供随机森林模型调参的参考，二来也是为了给读者展示随机森林算法在大型数据集上的强大威力。

9.5.1 otto数据集介绍

Otto Group数据集来源于《Otto Group Product Classification Challenge》。Otto集团是世界上最大的电子商务公司之一，在20多个国家拥有子公司，规模非常庞大。该集团每天在全球销售数百万种产品，因此，对该公司的产品性能进行一致性分析有利于该公司对各种商品的销售情况有个全局的认识。然而，由于商品种类数量过多，分布较分散，且该公司在全球各地的基础设施不同，导致许多相同种类的产品被划分为不同的种类，进而导致分类类别过多，给产品的分析造成了很多不便。为了给产品分析提供更大的便利，该公司从世界各地抽取了六万多件产品，为每件商品制定了93个评估指标作为数据集的特征，并按照这93个指标值的分配情况将所有商品划分为9个主要类别。该公司希望以这六万多件商品作为训练数据集，学习出一个能够准确预测该公司在全球200000种产品的主要类别的模型。由于模型的好坏直接影响集团的经济利益，因此我们要训练出一个验证准确率尽可能高的模型。同时，受限于我们个人计算机的计算资源，我们还希望在尽量提升模型拟合效果好坏的同时又能够尽量减少模型拟合的时间。下面就让我们来一起探索这个问题。

9.5.2 数据集的加载与查看

首先我们来加载一下这个数据集，对该数据集有个直观的认识。代码如下：

import pandas as pd
# 加载csv类型的数据集，并转化为DataFrame格式
df = pd.read_csv('./train.csv')
# 打印出训练数据集的后面5行
df.tail()

输出结果如下：

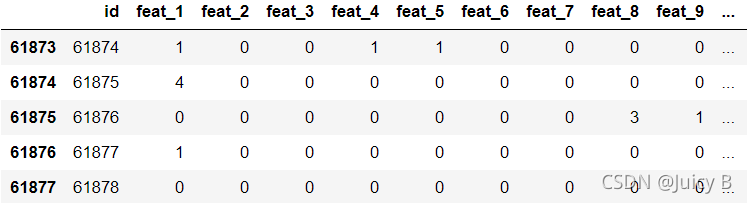
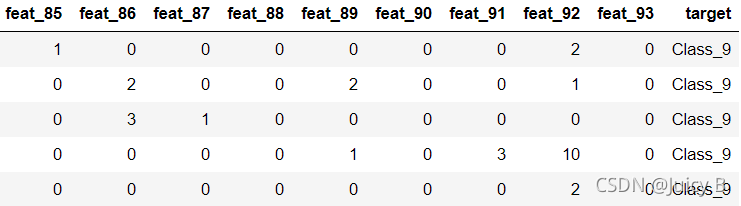
该商品数据集一共有9个类别，标签分别为class_1到class_9，每件商品拥有93个特征。查看完数据集之后，下面我们来定义一个加载该数据集的函数。代码如下：

# 定义加载数据集的函数
def get_dataset():
    data = pd.read_csv('./train.csv')
    dataset = data.values
    # 获取各个样本的数据
    X = dataset[: , :94]
    # 获取各个样本的标签
    y_ = dataset[: ,94 ]
    # 由于标签是字符串类型，所以要用LabelEncoder类转化为数字类型
    y = LabelEncoder().fit_transform(y_)
    return X, y

由于该数据集各个特征的分布很稀疏，有大量特征的数值为0的情况，所以在不对该数据集做进行进一步特征提取的前提下，使用随机森林模型来拟合该数据集是比较好的选择。下面我们就将使用随机森林对该训练数据集进行拟合。

9.5.3 交叉验证方法的定义

为了能够较好地评估模型对数据集的拟合效果，我们需要使用交叉验证方法，所以需要先定义交叉验证方法。代码如下：

def evaluate_model_with_accuracy(model):
    # 每个模型用10折交叉验证，重复3次
    cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
    # 以分类准确率作为交叉验证的指标
    scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
    return scores_acc

9.5.4. max_samples的探索

由于本例中数据集过于庞大，并且随机森林本身是一个比较复杂的算法，需要调整的参数较多，因此想要通过大规模的网格搜素来进行调参是不切实际的。所以我们选择对各个参数进行单独探索，大幅缩小每个参数的搜素范围，然后再进行网格搜素，这样能够大幅节省计算资源。先从max_samples参数开始。

该训练数据集有多达60000多个样本，数量非常庞大。那是不是所有的样本都要用来训练随机森林模型呢？训练样本数过少，模型容易欠拟合；训练样本数过多，模型的训练时间过长。因此我们需要在拟合时间拟合效果之间找到平衡。下面将分别取不同的训练样本比例，用这些数量不同的训练样本分别训练不同的随机森林模型，并对各个模型进行交叉验证，确定合适的训练样本数。我们将这一过程封装成一个函数，便于调用。代码如下：

# 定义一个获取模型列表的函数
def get_different_sample_nums_models():
    # 定义一个空字典，用于建立训练样本数与模型之间的映射
    models = dict()
    # 定义训练样本数占总样本数的比例
    percentages = np.arange(0.1, 1.0, 0.1)
    # 建立起不同训练样本数与对应随机森林模型之间的映射
    for per in percentages:
        models[str(int(X.shape[0] * per))] = RandomForestClassifier(max_samples=per)
    # max_samples=None表示不限制训练样本数，即所有的样本都用于随机森林的训练
    models[X.shape[0]] = RandomForestClassifier(max_samples=None)
    return models

到目前为止，我们一个定义了三个函数，分别为加载数据集的函数、定义交叉验证方法的函数、建立训练样本数与随机森林模型之间映射关系的函数。下面我们将调用这三个函数，获取不同模型在不同样本数量的数据集上的交叉验证结果。代码如下：

# 加载数据集
X, y = get_dataset()
# 获取随机森林模型列表
models0 = get_different_sample_nums_models()
# 定义三个列表，分别用于记录交叉验证准确率、训练样本数和拟合时间
results, names, times = [], [], []
for name, model in models0.items():
    time1 = time.time()
    # 获取模型列表中各个模型的交叉验证准确率
    scores_acc = evaluate_model_with_accuracy(model)
    time2 = time.time()
    total_time = time2 - time1
    results.append(scores_acc)
    names.append(name)
    times.append(total_time)
    # 打印出训练样本数、对应模型的交叉验证准确率和拟合时间
    print('Number of Samples for Each Training: %s , Validation Accuracy: %.3f (%.3f), Total Time: %.3f s' 
          % (name, mean(scores_acc), std(scores_acc), total_time))

输出结果如下（其中括号内的值表示交叉验证过程中多个中间验证结果的标准差）：

Number of Samples for Each Training: 6187 , Validation Accuracy: 0.983 (0.002), Total Time: 35.799 s
Number of Samples for Each Training: 12375 , Validation Accuracy: 0.989 (0.002), Total Time: 49.404 s
Number of Samples for Each Training: 18563 , Validation Accuracy: 0.992 (0.001), Total Time: 66.048 s
Number of Samples for Each Training: 24751 , Validation Accuracy: 0.993 (0.002), Total Time: 79.178 s
Number of Samples for Each Training: 30939 , Validation Accuracy: 0.993 (0.001), Total Time: 98.228 s
Number of Samples for Each Training: 37126 , Validation Accuracy: 0.994 (0.001), Total Time: 107.632 s
Number of Samples for Each Training: 43314 , Validation Accuracy: 0.994 (0.001), Total Time: 123.517 s
Number of Samples for Each Training: 49502 , Validation Accuracy: 0.995 (0.001), Total Time: 138.335 s
Number of Samples for Each Training: 55690 , Validation Accuracy: 0.995 (0.001), Total Time: 143.154 s
Number of Samples for Each Training: 61878 , Validation Accuracy: 0.995 (0.001), Total Time: 151.415 s

上述输出结果分为两部分：

拟合时间。

随着训练样本数的增加，所需要的拟合时间也越来越多，但是每增加10%的样本，平均拟合时间只多了十几秒，如果增加样本数对模型的拟合效果有提升作用，那么多出来的这点时间显然是值得的。
所有中间交叉验证准确率的平均值和标准差。

可以看到，当训练样本数量增加到49502时，中间交叉验证准确率的均值趋近于0.995，而标准差趋近于0.001，并不能看不出差距，所以此时单单从交叉验证准确率的数值指标来确定训练样本数是不够的，我们还需要将中间交叉验证准确率进行可视化，观察它们的分布状况，从稳定性的角度来确定训练样本数。因此，下面我们将绘制出中间交叉验证准确率的箱型图。代码如下：

plt.boxplot(results, labels=names, showmeans=True)
plt.xticks(rotation=45)
plt.show()

结果图如下：

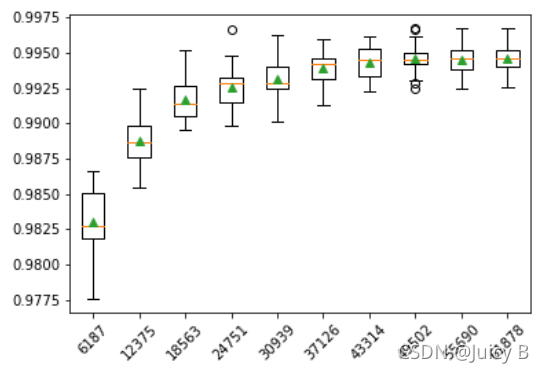
该箱型图的详细含义如下：

第一四分位数 (Q1)又称“下四分位数”，位于方块的下边缘，表示模型在数据集上中的所有中间交叉验证准确率从小到大排列后位于第25%的数值；
第二四分位数 (Q2)又称“中位数”，位于方块中间的红线处，表示模型在数据集上中的所有中间交叉验证准确率从小到大排列后位于第50%的数值；
第三四分位数 (Q3)又称“上四分位数”，位于方块的上边缘，表示模型在数据集上中的所有中间交叉验证准确率从小到大排列后位于第75%的数值；
绿色三角形表示各个模型的所有中间交叉验证准确率的平均值；
垂直于方块上边缘的那条线段的顶点称为”上限“，表示所有交叉验证准确率中的最大值；
垂直于方块下边缘的那条线段的顶点称为”下限“，表示所有交叉验证准确率中的最小值；
小圆点表示异常值。

通过观察该箱型图，可以发现，随着训练样本数的增加，中间交叉验证准确率整体的数据分布有越来越紧凑的趋势，在平均交叉验证准确率非常接近的情况下，分布越紧凑，说明模型的多次交叉验证准确率之间越接近，模型的抗干扰能力越强。而且可以看到，增加训练样本数并不会增加过多的拟合时间。在综合考虑了拟合时间、平均验证准确率和中间验证准确率分布之后，这里选择将数据集中的所有样本均作为训练数据集。

9.5.5 max_features的探索

前面已经介绍到，训练随机森林基学习器用的是在数据集中随机选择的一个包含 $k$ 个特征的子集，这个 $k$ 的取值通常为 $log_2d$ （ $d$ 为总特征数）。RandomForestClassifier中用max_features参数表示 $k$ 。本数据集中总的特征数为93，因此我们可以尝试在 $k = 8$ 附近做网格搜素，找到合适的 $k$ 值。首先定义一个函数，用于建立不同max_features取值与对应随机森林模型的映射关系。代码如下：

def get_different_features_nums_models():
    models = dict()
    max_features_nums = [6, 8, 10, 12, 14]
    for mfn in max_features_nums:
        models[str(mfn)] = RandomForestClassifier(max_features=mfn)
    return models

接下来获取各个模型在不同max_feature取值下在数据集上的交叉验证结果。代码如下：

# 加载数据集
X, y = get_dataset()
# 获取不同max_feature取值的随机森林模型列表
models1 = get_different_features_nums_models()
# 获取模型列表中各个模型的交叉验证准确率、max_features值和拟合时间  
results, names, times = [], [], []
for name, model in models1.items():
    time1 = time.time()
    scores_acc = evaluate_model_with_accuracy(model)
    time2 = time.time()
    total_time = time2 - time1
    results.append(scores_acc)
    names.append(name)
    times.append(total_time)
    # 打印出max_features值、对应模型的交叉验证准确率和拟合时间 
    print('Number of Max Features for Each Eplit Point: %s , Validation Accuracy: %.4f (%.4f), Total Time: %.4f s' 
          % (name, mean(scores_acc), std(scores_acc), total_time))

输出结果如下：

Number of Max Samples for Each Eplit Point: 6 , Validation Accuracy: 0.9849 (0.0021), Total Time: 125.6391 s
Number of Max Samples for Each Eplit Point: 8 , Validation Accuracy: 0.9927 (0.0014), Total Time: 139.5411 s
Number of Max Samples for Each Eplit Point: 10 , Validation Accuracy: 0.9964 (0.0008), Total Time: 158.3088 s
Number of Max Samples for Each Eplit Point: 12 , Validation Accuracy: 0.9979 (0.0006), Total Time: 168.7095 s
Number of Max Samples for Each Eplit Point: 14 , Validation Accuracy: 0.9988 (0.0005), Total Time: 181.5990 s

同样画出箱型图，代码如下：

plt.boxplot(results, labels=names, showmeans=True)
plt.show()

输出结果如下：

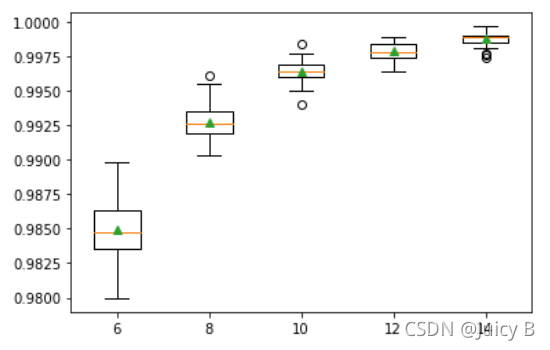
可以看到，随着max_features取值的增加，平均验证准确率在不断上升，中间验证准确率的分布也有越来越紧密的趋势，说明将max_features取为更大的值还可以进一步提升模型的表现。所以下面再分别取max_features=16, 18, 20, 22, 24，对各个模型进行拟合，并绘制验证曲线。代码如下：

max_features_range = [16, 18, 20, 22, 24]
train_scores, validation_scores = validation_curve(
                estimator=RandomForestClassifier(), 
                X=X, 
                y=y, 
                param_name='max_features',     
                param_range=max_features_range,                   
                cv=10,                                                   
                n_jobs = -1)                                                      

train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
validation_mean = np.mean(validation_scores, axis=1)
validation_std = np.std(validation_scores, axis=1)

plt.plot(max_features_range, train_mean, color='blue', marker='o',  markersize=5, label='training accuracy')

plt.fill_between(max_features_range, train_mean + train_std,train_mean - train_std, 
                 alpha=0.1, color='blue')

plt.plot(max_features_range, validation_mean, color='green', linestyle='--', marker='s', 
         markersize=5, label='validation accuracy')

plt.fill_between(max_features_range, validation_mean + validation_std,validation_mean - validation_std, 
                 alpha=0.15, color='green')

plt.grid()
plt.legend(loc='lower right')
plt.xlabel('CountVectorizer min_df')
plt.ylabel('Accuracy')
plt.ylim([0.8, 1.03])
plt.tight_layout()
plt.show()

输出结果如下：

Number of Max Samples for Each Eplit Point: 16 , Validation Accuracy: 0.9993 (0.0004), Total Time: 199.0818 s

Number of Max Samples for Each Eplit Point: 18 , Validation Accuracy: 0.9996 (0.0002), Total Time: 206.2730 s

Number of Max Samples for Each Eplit Point: 20 , Validation Accuracy: 0.9997 (0.0002), Total Time: 220.8178 s

Number of Max Samples for Each Eplit Point: 22 , Validation Accuracy: 0.9998 (0.0002), Total Time: 246.3433 s

Number of Max Samples for Each Eplit Point: 24 , Validation Accuracy: 0.9999 (0.0001), Total Time: 257.3168 s

可以看到，当随着max_features的进一步增加，中间验证准确率的平均值还在逐渐升高，标准差也在继续降低，所以最佳的max_features取值一定在更大的范围里。但是随着max_features值的增加，验证准确率的平均值一定会趋于收敛，增加max_features的值对模型拟合效果的提升作用也会越来越小，拟合时间也会逐渐增加，所以将max_depth没必要设置得过大。因此，这里选择将max_features的搜素范围设置为[26, 28, 30]，而没有设置更大的值。

9.5.6 n_estimators的探索

n_estimators参数表示随机森林的迭代次数，亦即基决策树的棵数。该参数对模型拟合效果的影响很大，是调参的重点对象。代码如下：

# 建立不同n_estimators取值与对应随机森林模型的映射关系
def get_different_n_estimators_models():
    models = dict()
    n_estimators_nums = [10, 50, 100, 200, 500]
    for nen in n_estimators_nums:
        models[str(nen)] = RandomForestClassifier(n_estimators=nen)
    return models 

# 加载数据集
X, y = get_dataset()
# 获取不同n_estimators取值下的随机森林模型列表
models2= get_different_n_estimators_models()
# 获取模型列表中各个模型的交叉验证准确率、n_estimators值和拟合时间  
results, names, times = [], [], []
for name, model in models2.items():
    time1 = time.time()
    scores_acc = evaluate_model_with_accuracy(model)
    time2 = time.time()
    total_time = time2 - time1
    results.append(scores_acc)
    names.append(name)
    times.append(total_time)
    # 打印出n_estimators值、对应模型的交叉验证准确率和拟合时间 
    print('Number of Trees: %s , Validation Accuracy: %.4f (%.4f), Total Time: %.4f s' 
          % (name, mean(scores_acc), std(scores_acc), total_time))

输出结果如下：

Number of Trees: 10 , Validation Accuracy: 0.9848 (0.0036), Total Time: 26.9640 s
Number of Trees: 50 , Validation Accuracy: 0.9941 (0.0012), Total Time: 78.8526 s
Number of Trees: 100 , Validation Accuracy: 0.9947 (0.0010), Total Time: 145.1331 s
Number of Trees: 200 , Validation Accuracy: 0.9953 (0.0010), Total Time: 282.7573 s
Number of Trees: 500 , Validation Accuracy: 0.9955 (0.0009), Total Time: 736.4792 s

画出箱型图：

plt.boxplot(results, labels=names, showmeans=True)
plt.xticks(rotation=45)
plt.show()

结果如下：

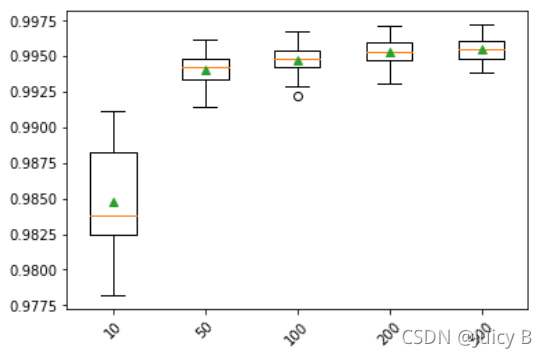
当n_estimators取值不大于200的情况下，提升迭代次数对模型拟合效果的提升作用较为明显。但对比n_estimators=200和n_estimators=500的情况，可以发现，取值为500比取值为200的拟合时间增加了大约两倍，但平均验证准确率只增加了0.0002。因此，在综合考虑拟合效果和拟合时间的前提下，选择n_estimators的搜素范围为200到300之间相对较合理，暂定为[200, 250, 300]。

9.5.7 max_depth的探索

基决策树的最大深度max_depth也是随机森林模型拟合效果的一大影响因素，因此需要对该参数进行探索。代码如下：

def get_different_tree_depth_models():
    models = dict()
    tree_depth_nums = np.arange(1, 8)
    for tdn in  tree_depth_nums:
        models[str(tdn)] = RandomForestClassifier(max_depth=tdn)
    models['None'] = RandomForestClassifier(max_depth=None)
    return models

X, y = get_dataset()

models3 = get_different_tree_depth_models()
results, names, times = [], [], []
for name, model in models3.items():
    time1 = time.time()
    scores_acc = evaluate_model_with_accuracy(model)
    time2 = time.time()
    total_time = time2 - time1
    results.append(scores_acc)
    names.append(name)
    times.append(total_time)
    print('Number of Maximun Tree Depth: %s , Validation Accuracy: %.4f (%.4f), Total Time: %.4f s' 
          % (name, mean(scores_acc), std(scores_acc), total_time))

输出结果如下：

Number of Maximun Tree Depth: 1 , Validation Accuracy: 0.4593 (0.0069), Total Time: 35.6627 s
Number of Maximun Tree Depth: 2 , Validation Accuracy: 0.5230 (0.0100), Total Time: 44.2107 s
Number of Maximun Tree Depth: 3 , Validation Accuracy: 0.5957 (0.0268), Total Time: 56.0701 s
Number of Maximun Tree Depth: 4 , Validation Accuracy: 0.7141 (0.0480), Total Time: 65.2183 s
Number of Maximun Tree Depth: 5 , Validation Accuracy: 0.8004 (0.0212), Total Time: 74.8410 s
Number of Maximun Tree Depth: 6 , Validation Accuracy: 0.8444 (0.0100), Total Time: 92.1092 s
Number of Maximun Tree Depth: 7 , Validation Accuracy: 0.8716 (0.0074), Total Time: 94.1047 s
Number of Maximun Tree Depth: None , Validation Accuracy: 0.9949 (0.0010), Total Time: 145.1572 s

plt.boxplot(results, labels=names, showmeans=True)
plt.show()

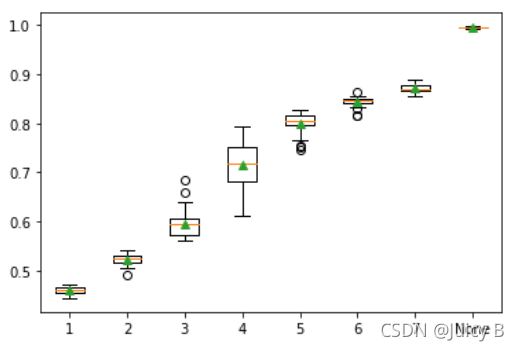
可以看到，在不限制基决策树最大深度的情况下模型的拟合效果比限制基决策树最大深度要好得多，所以此处选择不对max_depth的取值进行限制。

9.5.8 根据上述结果选用相对合适的候选参数做网格搜索

经过前面的探索，我们得到：在各个参数分开探索的前提下，各参数较为合适的取值为：

max_depth = None
max_samples = None

经过我们上面的分析，以上这两个参数均使用默认值，表示不限制基决策树的最大深度、训练样本数等于数据集的样本数，因此不再进行网格搜素。而对于n_estimators和max_features的搜素范围为：

n_estimators $\in$ [200, 250, 300]
max_features $\in$ [26, 28, 30]

下面我们将在上面所定义的各个参数范围的基础上进行网格搜素。代码如下：

max_features = [26, 28, 30]
n_estimators = [200, 250, 300]

param_grid = dict(max_features=max_features, n_estimators=n_estimators)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=5)

model = RandomForestClassifier()

grid_search = GridSearchCV(model, param_grid=param_grid, scoring="accuracy", n_jobs=-1, cv=kfold,
                          verbose=1)
grid_result = grid_search.fit(X, y)
print("Best: %f using %s" % (grid_result.best_score_, grid_result.best_params_))
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, std, param in zip(means, stds, params):
    print("%f (%f) with: %r " % (mean, std, param))

输出结果如下：

Fitting 10 folds for each of 9 candidates, totalling 90 fits

[Parallel(n_jobs=-1)]: Using backend LokyBackend with 8 concurrent workers.
[Parallel(n_jobs=-1)]: Done  34 tasks      | elapsed: 12.8min
[Parallel(n_jobs=-1)]: Done  90 out of  90 | elapsed: 31.4min finished

Best: 0.999935 using {‘max_features’: 28, ‘n_estimators’: 250}
0.999887 (0.000103) with: {‘max_features’: 26, ‘n_estimators’: 200}
0.999855 (0.000113) with: {‘max_features’: 26, ‘n_estimators’: 250}
0.999887 (0.000074) with: {‘max_features’: 26, ‘n_estimators’: 300}
0.999903 (0.000107) with: {‘max_features’: 28, ‘n_estimators’: 200}
0.999935 (0.000079) with: {‘max_features’: 28, ‘n_estimators’: 250}
0.999903 (0.000079) with: {‘max_features’: 28, ‘n_estimators’: 300}
0.999887 (0.000145) with: {‘max_features’: 30, ‘n_estimators’: 200}
0.999903 (0.000107) with: {‘max_features’: 30, ‘n_estimators’: 250}
0.999887 (0.000126) with: {‘max_features’: 30, ‘n_estimators’: 300}

可以看到，在max_depth和max_samples均使用默认值时，最佳参数组合为max_features=28, n_estimators=250，两个参数的取值均位于各自搜素区间的中间，并且模型达到了99.9935%的平均验证准确率。这说明了我们上面的调参探索思路的正确性，也展示了随机森林模型在处理稀疏、大型数据集上的强大能力。