做习题，学知识--线索二叉树

二叉树在线索化后，仍不能有效求解的问题是（）

A、先序线索二叉树中求先序后继    

B、中序线索二叉树中求中序后继

C、中序线索二叉树中求中序前驱    

D、后序线索二叉树中求后序后继

因为有同学问到：线索二叉树的结构不是会多出两个指针域来存放前驱和后继的吗？

那么我们先来看看在严蔚敏老师的数据结构教材中对线索二叉树的定义：

从书中我们可以得出，线索二叉树的确多出了两个指针域 LTag 和 RTag，但不是用来存放结点前驱、后继，而是指示左右孩子是否存在。

那么我们开始分析题目：

首先，我们要先对树的遍历有一定的了解，不清楚的伙伴可以查看我的历史文章 【数据结构】二叉树的中序遍历 。

先序遍历（中左右）、中序遍历（左中右）的最后访问的节点都是左或右叶节点，叶节点是没有子树的，所以两个指针域空出来了，可以存放线索指针。但是后序遍历（左右中），最后访问的是子树的根节点，而子树根节点的指针域指向了子树，所以不可能空出来存放线索信息。

举个例子：

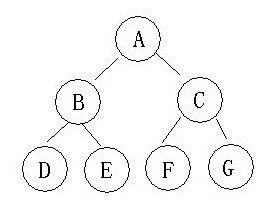
对于上面这棵树，它的遍历结果是这样子的：

先序遍历：A->B->D->E->C->F->G
中序遍历：D->B->E->A->F->C->G
后序遍历：D->E->B->F->G->C->A

A选项中，
结点 A->B->D 这串可以从子指针得到
结点 D->E->C 由于子指针是空的，可以从子指针生成线索

结点 C->F->G 由上可得

同理，也能解得 B、C 选项的正确性。

而对于 D 选项，

结点 C->A 是不可能达到，因为结点 C 的左右儿子都是满的，已经没有地方存线索，所以不可能线索化。

因此答案就出来了：选 D 。