补充知识
- 玩转数据结构 从入门到进阶 里面有很详细的数组、栈、队列、链表、二分搜索树、集合和映射、堆、线段树、Trie、并查集、AVL、红黑树、哈希表的教程。很详细!。
- B树和B+树的插入、删除图文详解
- 图解B+树的插入和删除(一看就懂)
查找的基本概念
1. 关键码
可以标识一个记录的某个数据项
- 主关键码:可以唯一地标识一个记录的关键码。如学号
- 次关键码:不能唯一地标识一个记录的关键码。如姓名
2. 查找
静态查找:对表的操作不会改变查找表。
适用于:查找集合一经生成,便只对其进行查找,而不进行插入和删除操作,或经过一段时间的查找之后,集中地进行插入
和删除等修改操作。
动态查找:对表的操作会改变查找表
适用于:查找与插入和删除操作在同一个阶段进行,例如当查找成功时,要删除查找到的记录,当查找不成功时,要插入被查找的记录。
3.查找结构
面向查找操作的数据结构,即查找基于的数据结构
线性表:适用于静态查找(顺序查找、折半查找)
树:适用于动态查找(二叉排序树上的查找)
散列表:适用于静、动态查找(散列查找)
4. 平均查找长度ASL
查找算法时间性能通过关键码的比较次数来度量。
定义:查找成功时,ASL是为确定数据元素在表中的位置所进行的关键码比较次数的期望值。
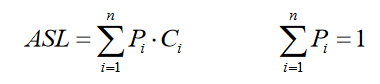
含义:
n :查找表含n个数据元素
Pi :表中第i个数据元素的查找概率
Ci :表中第i个数据元素的关键码与给定值Kx相等,按某算法查找时关键码的比较次数。
不同查找算法Ci不同
二、静态查找
1. 顺序查找
基本思想
从线性表的一端向另一端逐个将关键码与给定值进行比较
- 若相等,则查找成功,给出该记录在表中的位置;
- 若整个表检测完仍未找到与给定值相等的关键码,则查
找失败,给出失败信息。
我们通过设置"哨兵"免去了在查找过程中每一次比较都要判断查找位置是否越界,提高查找效率。
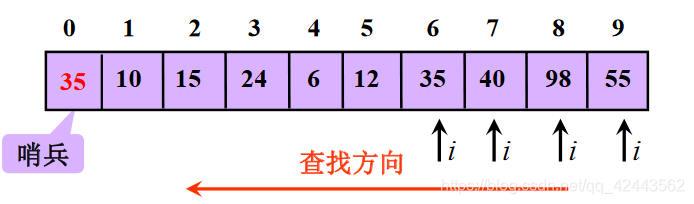
实现算法
数据类型表述
typedef struct
{
DataType data[MaxSize]; //查找表存储空间的基地址
int length; //查找表的长度
}S_T;
int S_Search(S_T *t,KeyType kx){
//在表t中查找关键字为kx的数据元素,若找到返回该元素在数组中的下标,否则返回0
int i ;
t->data[0].key = kx;
//存放检测,这样在从后向前查找失败时,不必判断表是否检测完,从而达到算法统一
for(i = t->length;t->data[i].key != kx;i--); //从表尾端向表前查找
return i;
}
性能分析
查找成功时,平均长度为(等概率):(n+1)/2
查找失败时,关键码的比较数总是n+1次
时间复杂度为:O(n);
算法特点
优点
- 算法简单
- 对记录的存储没有要求,顺序存储、链式存储均可
- 对记录的有序性没有要求,无论记录是否有序均可
缺点
- n较大时,ASL较大,算法效率低
算法适用范围
顺序存储、链式存储
2.折半查找
基本思想
在有序表中,取中间元素作为比较对象
- 若给定值与中间元素的关键码相等,则查找成功
- 若给定值小于中间元素的关键码,则在中间元素的左半区继续查找
- 若给定值大于中间元素的关键码,则在中间元素的右半区继续查找
- 重复上述查找过程,直到查找成功,或所查找的区域无数据元素,查找失败。
例:查找值为22的记录过程
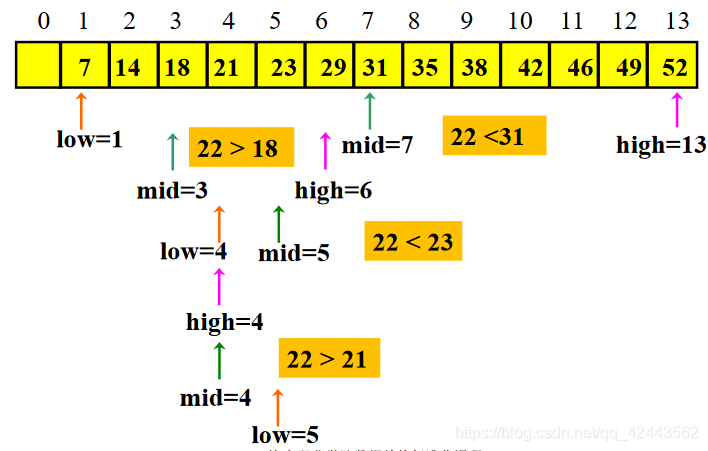
实现算法
int Binary_Search(S_T *t,KeyType kx){
/*在表t中查找关键码为kx的数据元素,若找到返回该元素在表中的位置否则返回0*/
int low,high,mid;
int flag;
low = 1;
high = t->length; //设置初始区间
flag = 0;
while(low <= high) //表空测试
{
mid = (low+high)/2; //得到中点
if(kx < t->data[mid].key)
high = mid-1; //调整到左半区
else
if(kx > t->data[mid].key)
low = mid+1; //调整到右半区
else
{
flag = mid;
break; //查找成功,元素位置设置到flag中
}
}
return flag;
}
效率分析
从折半查找过程看,以表的中点为比较对象,并以中点将表分割为两个子表,对定位到的子表继续这种操作。所以,对表中每个数据元素的查找过程,可用二叉树来描述,称这个描述查找过程的二叉树为判定树。
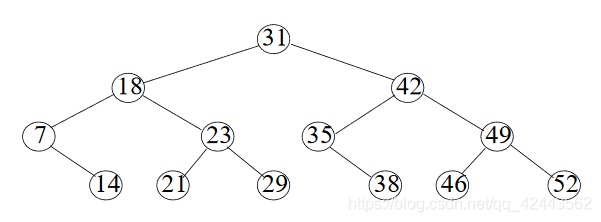
在折半查找成功时,关键码比较次数至多为 log 2 ( n + 1 ) \log_2 (n+1) log2(n+1)
折半查找的时间效率为O( log 2 n \log_2 n log2n)
适用范围
记录按关键码有序、顺序存储
算法特点
优点
- 时间效率高
缺点
- 要求数据元素顺序存储且关键码有序
3.分块查找
索引顺序表结构:
需要将文件划分为若干块,且要求分块有序。
这里不做要求,可自行学习。
小结
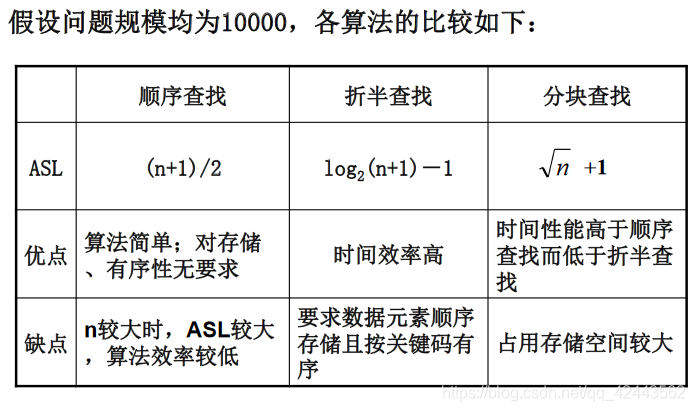
三、动态查找
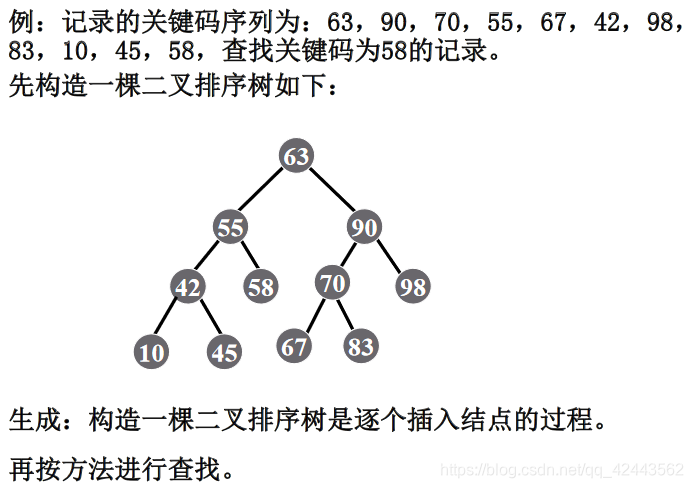
二叉树查找过程
- 若查找树为空,查找失败
- 查找树非空,将给定值kx与查找树的根节点关键码比较。
- 若相等,查找成功,结束查找过程:否则,
- 当给kx小于根节点关键码,查找将在左子树上继续进行,转1;
- 当给kx大于根节点关键码,查找将在右子树上继续进行,转1;
四、 散列查找
基本概念
-
哈希查找:是一种重要的存储方式,又是一种查找方法,又称散列
哈希表:按散列存储方式构造的动态表称为散列表,又称为哈希表
-
基本思想:已记录的关键字key为自变量通过一个确定的哈希函数H,计算出对用的函数值H(key)作为记录的存储地址。
哈希函数: 是哈希表查找的核心,用以计算记录的关键字在哈希表中的存储地址
哈希表的表示: 用一维数组H[0…m-1]表示,m为表长

- 冲突/碰撞
冲突的引入:不同关键字值具有相同的哈希地址的现象称为“冲突”或者“碰撞”
具有相同函数值的不同关键字称为“同义词” - 哈希查找考虑的主要问题
- 所选函数尽可能简单,以提高转换速度
- 所选函数对关键码计算出的地址,应在哈希地址中大致均匀分布,以减少空间浪费
- 制定解决冲突的方案
哈希函数的构造方法
- 直接定址法;
- 除留余数法:用模(%)运算得到哈希地址的方法,即散列函数为H(key) = key % p (p <= m)
- 随机数法
- 数字分析法
- 平方取中法
处理冲突的方法
开放定址法
当冲突发生时,形成一个探查序列,沿着这个序列逐个探测,直到找到一个“空”的开放地址,将发生冲突的关键字存放到该地址中去。
两种探测方法
- 线性探测法:增量序列为 di = 1,2,3…m-1
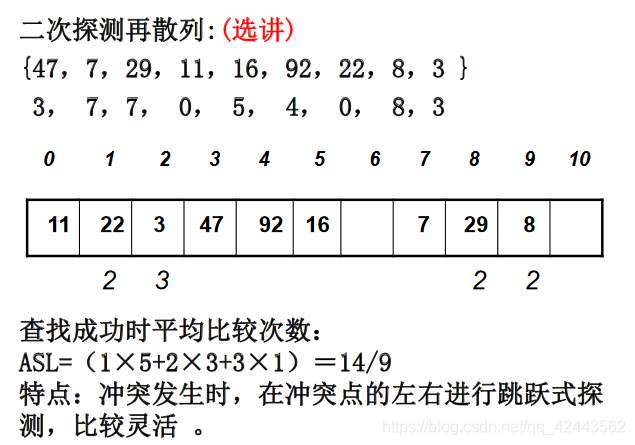
- 二次探测法:增量序列为 di = 12,-12,22,-22…
例:

特点
- 采用线性探测法解决冲突的方法思路清晰,算法简单
- 遇到冲突时,将产生冲突的记录再散列到离冲突点最近的空位置上,从而又增加了更多的冲突机会,这种现象称为聚集或者堆积
-
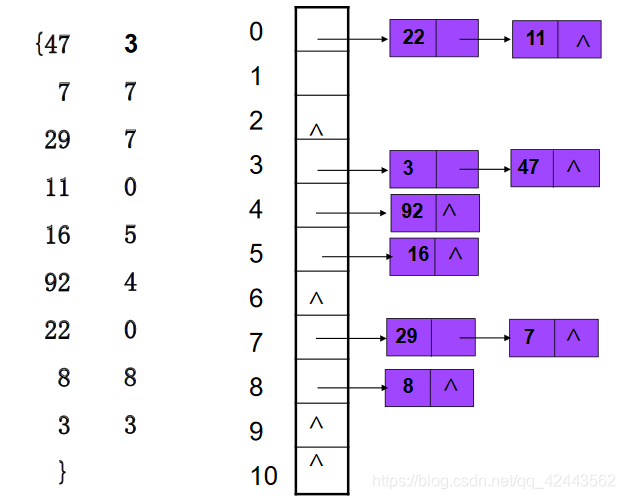
链地址法:是把具有相同哈希地址的关键字值存放在同一个链表中。
-
哈希表的每个单元不是存储相应的数据元素的关键码,而是存储相应单链表的表头指针。
-
单链表中的每个结点由动态分配产生,可以方便地插入和删除结点。
注意:在相同的哈希地址存放时,使用表头插入法
算法特点
优点: 能较好地解决溢出问题,易于实现删除操作
缺点: 存储空间需要增加一个链域;若哈希函数的均匀性较差,则会造成基本哈希表存储区中空闲单元较多。










 本文深入解析了数据结构中的查找算法,包括顺序查找、折半查找、分块查找等静态查找方法,以及二叉树查找、散列查找等动态查找方法。详细介绍了各种查找算法的基本思想、实现算法及效率分析。
本文深入解析了数据结构中的查找算法,包括顺序查找、折半查找、分块查找等静态查找方法,以及二叉树查找、散列查找等动态查找方法。详细介绍了各种查找算法的基本思想、实现算法及效率分析。
















 4655
4655

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








