数据结构之查找

常见查找算法

顺序查找

二分查找

索引查找

hash查找

主关键字:不能重复,唯一,比如id
次关键字:可能重复,比如姓名
查找表:

顺序查找:

空间复杂度:o(1)
时间复杂度:
最好:o(1)
最坏:o(n)
平均:o(n)

如果已知概率,可将大概率数据放在靠前,以减少平均查找长度

折半查找:

有序表:顺序表中的记录按照关键字值有序
时间复杂度:log(n)
以深度为h的满二叉树为例,即
$$n=2^h-1$$
并且查找概率相等,则ASL(平均查找长度)

$$ASL=\frac{1}{n}\sum _{j=1}^{h}j\ast 2^{j-1}=\frac{n+1}{n}\lg (n+1)-1$$
n>50时,得近似结果:
$$ASL=\lg (n+1)-1$$
注:lg 这里指2为底的对数
折半查找:只适用于有序表+顺序存储结构(不能用于链式存储结构,这点在面试题中常常会遇到)

索引查找

场景:数据量特别大
方法:

1. 先分析数据规律
2. 根据索引进行快速定位
3. 在定位的地方进行细致搜索

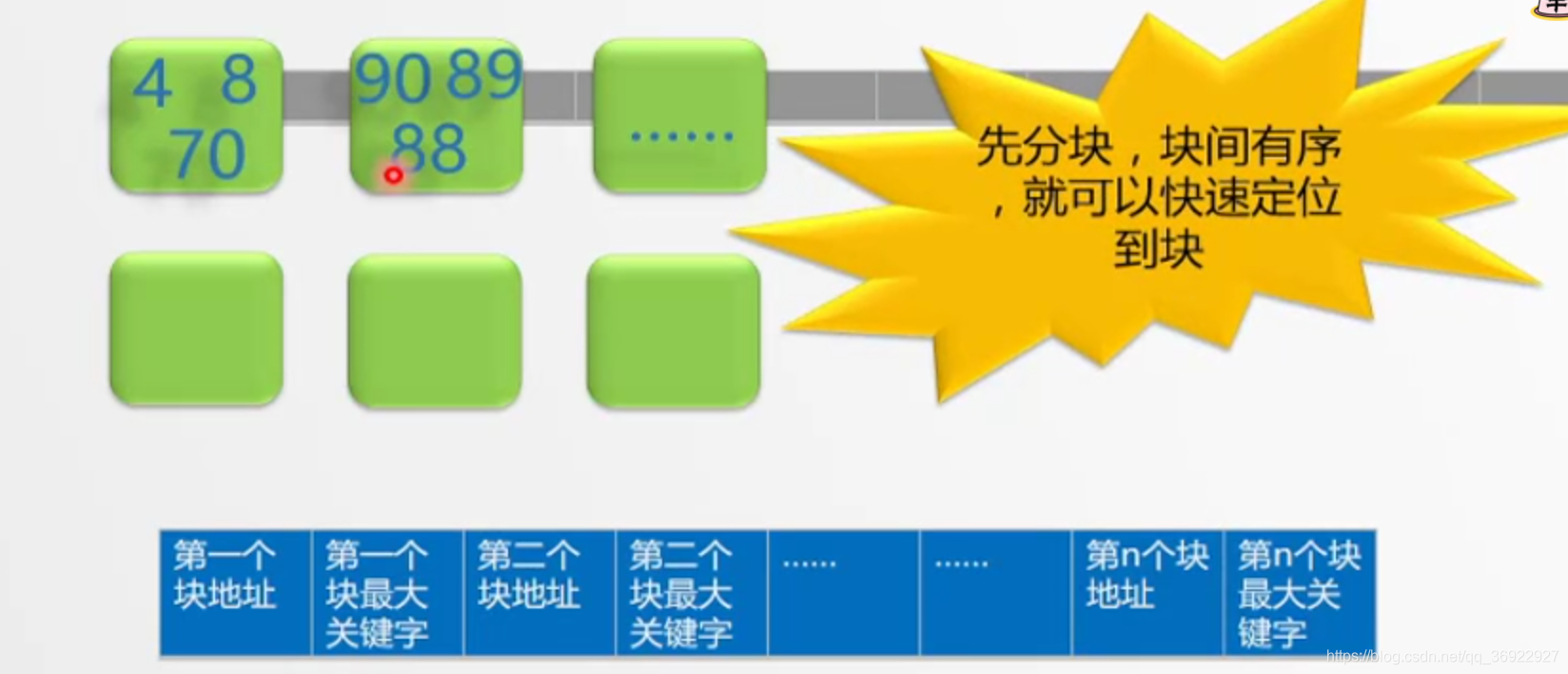
如下图:数据整体上是无序的,但是发现前三个元素的最大值比后三个元素都小
那么可以将前三个元素放到一块连续内存,并且记录下首地址和这块最大元素70
第二块最大元素是90
现在的索引建立如下:
第一块内存首地址->70->第二块内存首地址->90…
加入现在想要查找88
第一块最大值是70 ,那么88不可能在第一块内存
第二块内存最大值是90 ,并且90>70 ,88<90 ,这就说明,如果88存在那么就只可能在第二块连续内存中,现在只需要在第二块内存中查找88即可

又如:
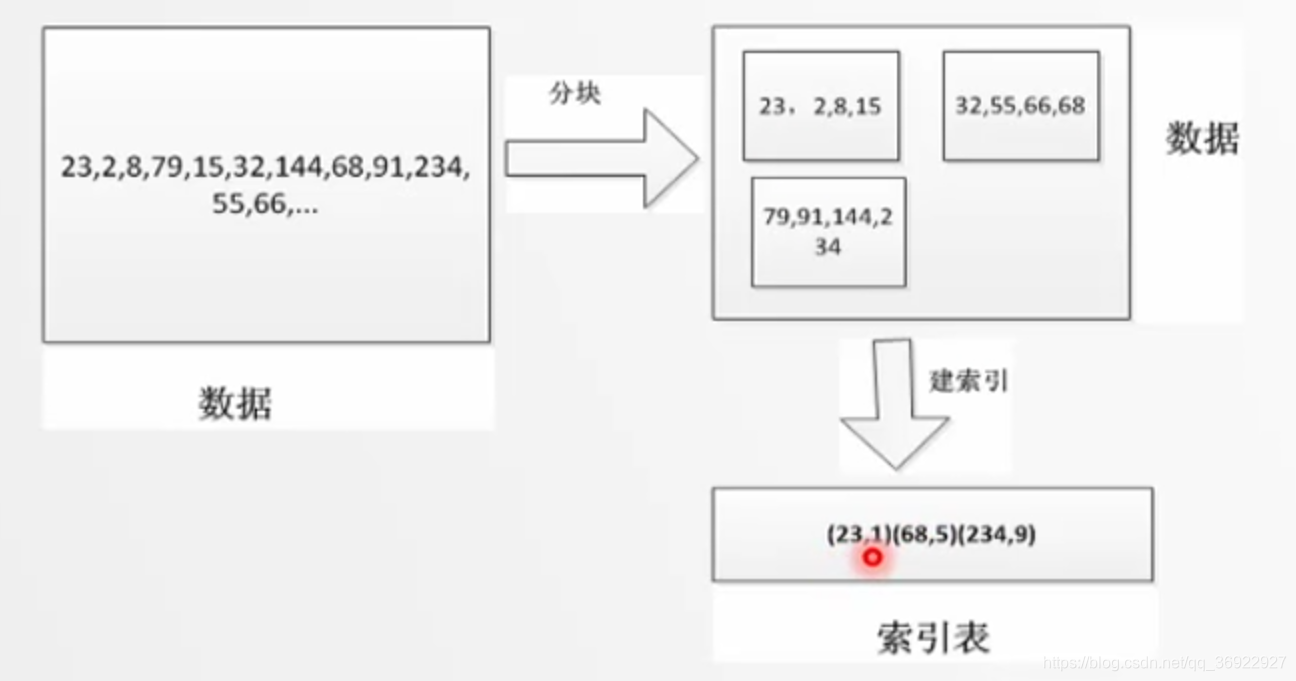### 流程:
1,根据比较关键字去定位可能存储该关键字的内存块
2,如果定位到内存块,执行块内查找 ¹
3,否则一直向后,直到预先设立的 第(n+1)块,标记索引结束位置,表示不存在该关键字
性能分析:块间查找+块内查找
块间是有序的,可以使用二分查找
块内无序,执行顺序查找

hash查找

Hash的思想:

例如新生学号是 xx000-xx999
要求查找:xx189号学生信息
如何高效查找呢?
给定后三位 189,
如何给内存地址与key值(后三位)建立一种映射,已知key就能获取到内存地址,
建立key与地址的映射关系

hash就是这样的思想
使用hash函数,将key映射到地址
address=hash(key)
但是需要考虑hash冲突
冲突是很难避免的,但是可以选择比较好的hash函数尽量减少冲突的发生
两个条件:

1. 计算简单
2. 冲突少

常见hash函数构造方法:

1. 直接hash:H(key)=c*key+d (hash函数是一个线性函数)
2. 数字分析法:比如n个d位数的关键字,由r个不同的符号组成,此r个符号在关键字各位出现的频率不一定相同,可能在某些位均匀分布,即每个符号的出现次数都接近与n/r,而在另一些位分布不均匀,则选择其中分布均匀的s位作为hash地址
   例如:
   
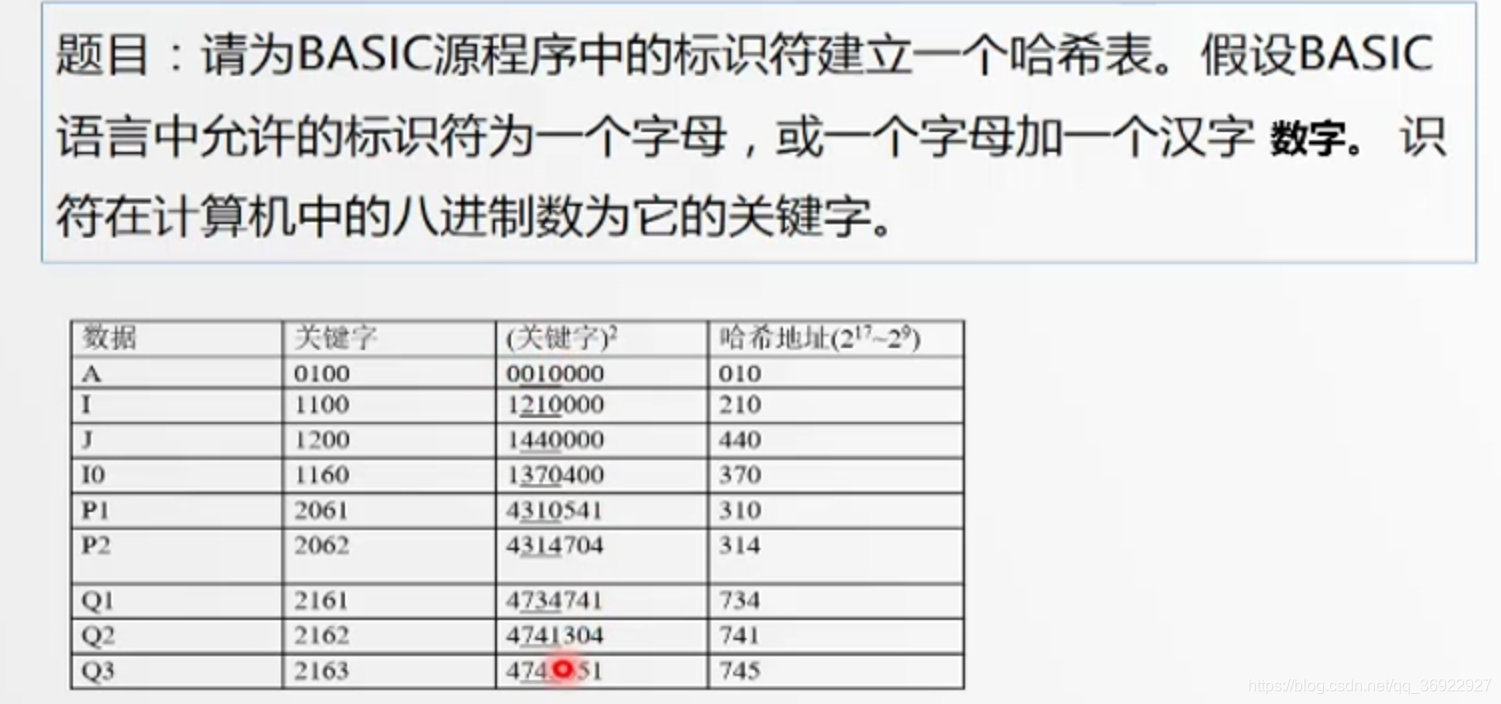
3. 平方取中:取关键字平方后的中间几位作为hash地址,所取的位数取决于hash表的大小.
   主要思想:以关键字的平方值的中间几位作为存储地址,求"关键字的平方值"目的是为了"扩大差别"和"贡献均衡"
   即关键字的各位都在平均值的中间几位有所贡献,Hash 值中应该有各位的影子.
   
4. 折叠法
   关键字的位数较长时,可将关键字分割成位数相等的几部分(最后一部分位数可以不同),取这几部分的叠加和(舍去高位的进位)作为hash地址,位数由存储地址的位数决定.具体来说,两种叠加方式:
   a. 移位叠加法:将每部分得到最后一位对齐,然后相加

b. 边界叠加法:把关键字看做一张纸条,从一端想另一端边界逐次折叠,然后对齐相加

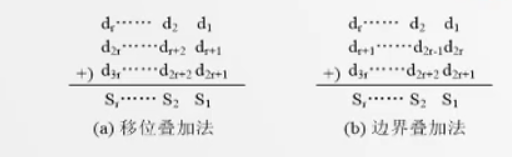
5. 除留余数
   取关键字被某个不大于hash表长度m的数p除后的余数作为hash地址,
   例如:m=17
   给定关键字:1,6,8,9,13,15,23,
   对应计算出的hash地址为:
   1,6,8,9,13,15,6
   发现关键字 6和23 出现冲突,p的选择则很重要,如果选取不当,会出现很多冲突
   比如关键字都是10的倍数,而p恰好为10,结果全部冲突
6. 随机数
   选择一个随机函数,取关键字的随机函数值作为hash地址
   (注意相同的key需要得到相同的hash值)
   hash函数选取需要考虑的因素:
   计算hash函数所需时间:(hash函数要简单)
   关键字长度:(是不是要分段)
   hash表大小:(处理所有)
   关键字的分布情况(均匀还是非均匀):
   记录的查找频率
   字符串的hash查找:
   比如单词的查找:
   name=since
   attribute=a list pf meaning:1,2,3,4,

hash 函数的属性:

1. 必须能够计算任意关键字且冲突最少

2. hash值应该均匀分布,比如对任意x和i,有如下概率:
   f(x)=i 的概率为 1/b,这种函数叫 均匀
   分布hash函数

   思考:如果 tablesize=10,而且key都是以0结尾的数呢?

   tablesize 选取质数
   

问题1:如何获取字符串的x???

字符是对应一个ascii码值,通过将ascii值相加得到x
取:tablesize=10007,字符串字符数<=8
每个ascii值 是0-127,f(x) 的范围是0-1016,发现大量数据会聚集在此区间,分布不够均匀
解决:把字符串的某些位扩大,比如将前三个字符的ascii分别 x1,x27${}^2$

问题2: 如何提高hash函数的运算速度?

解决: 高次幂的乘法运算效率很低,如果将 27替换成32(32是 2${}^k$,2的5次幂,相当于左移5位)
26*27${}^2$=18954(其中26是指26个字母),第三个字符就可以产生18954中组合的可能,但实际上一般是少于3000的

问题3 如果字符串很长呢?

比如当字符串是地址时,会出现较长长度的街道地址

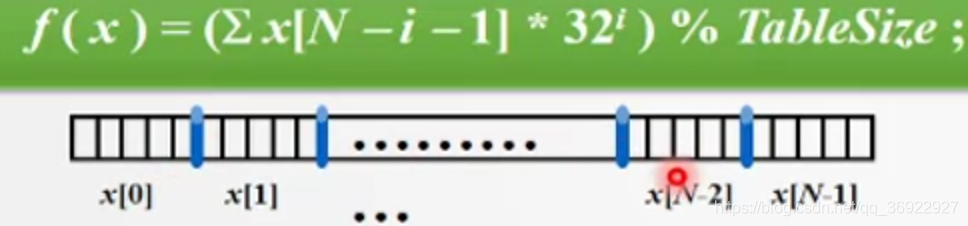
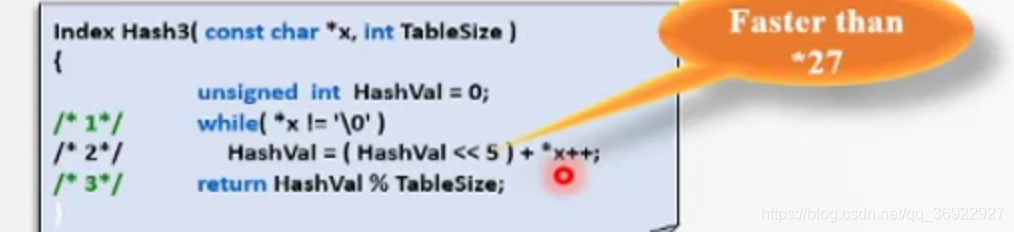
方法1:整体移位,比如整体左移,只保留特定长度位数运算取hash值
方法2:选取特定位置的字符取hash值(如x太长,比如街道地址,就选取其中比较特殊的几个位置来做hash运算)

hash 冲突:

冲突是指:由key计算出的hash地址已经存在记录
虽说好的hash函数,可以减少冲突,但是不能避免
冲突的处理:
为出现hash地址冲突的关键字寻找下一个hash地址
常用处理冲突法:

• 开放地址法:

• 为产生冲突的地址H(key) 求得一个地址序列:
  H${}_0$,H${}_1$,H${}_2$,H${}_3$,…,H${}_s$. 1$\le$s$\le$m-1
  注:H${}_0$=H(key)
  H${}_i$=(H(key)+d${}_i$)MODm
  i=1,2,3,…,s
  H${}_i$ 为第i次冲突的地址,i=1,2,…,s
  **H(key)**为Hash函数值
  m 为Hash 表表长
  d${}_i$ 为增量序列
  根据 d${}_i$ 的不同选取方式,又有以下三种方式:

• 线性探测再散列
  d${}_i$=c*i, 最简单的情况c=1(冲突次数会比较多,容易出现聚集,已存储数据接近表长1半时,应该建立新表)

• 平方探测在散列
  d${}_i$=1${}^2$,-1${}^2$,2${}^2$,-2${}^2$,…,

• 随机探测再散列
  d${}_i$ 是一组伪随机数列

demo:给定关键字集合如下:

{19,01,23,14,55,68,11,82,36}
设定hash函数H(key)=key MOD 11(表长为11)
如果采用 线性探测再散列处理冲突
H(19)=8
H(01)=1
H(23)=1(冲突)
H(23)=(23+1)MOD11=2
H( 14)=3
H(55)=0
H(68)=2(冲突)
H(68)=(68+1)MOD 11=3(冲突)
H(68)=(68+2)MOD11=4
H(11)=0(冲突)
H(11)=(11+1)MOD 11=1(冲突)
H(11)=(11+2)MOD 11=2(冲突)
H(11)=(11+3)MOD 11=3(冲突)
H(11)=(11+4)MOD 11=4(冲突)
H(11)=(11+5)MOD 11=5
H(82)=5(冲突)
H(82)=(82+1)MOD 11=6
H(36)=3(冲突)
H(36)=(36+1)MOD 11=4(冲突
)
H(36)=(36+2)MOD 11=5(冲突)
H(36)=(36+3)MOD 11=6(冲突)
H(36)=(36+4)MOD 11=7

0	1	2	3	4	5	6	7	8	9	10
55	01	23	14	68	11	82	36	19
1	1	2	3	1	2	1	0	0

最后一行是冲突次数:
查找成功的ASL:
ASL(成功)=(1+1+2+3+1+2+1+0+0)/9=11/9
查找失败的ASL:
ASL(失败)=(9+8+7+6+…+2+1)/11=45/11
如果key的hash值不在0-9,那么0次就失败
如果key的hash值为0,1,2,3,4,…,9
分别需要9,8,7,6,5,4,3,2,1 查找比较才能得出查找失败的结论

如果采用二次探测再散列:
H(19)=8
H(01)=1
H(23)=1(冲突)
H(23)=(23+1${}^2$)MOD11=2
H(14)=3
H(55)=0
H(68)=2(冲突)
H(68)=(68+1${}^2$)MOD11=3(冲突)
H(68)=(68+2${}^2$)MOD11=6
H(11)=0(冲突)
H(11)=(11+1${}^2$)MOD11=1(冲突)
H(11)=(11+2${}^2$)MOD11=4
H(82)=5
H(36)=3(冲突)
H(36)=(36+1${}^2$)=4(冲突)
H(36)=(36+2${}^2$)=7

0	1	2	3	4	5	6	7	8	9	10
55	01	23	14	11	82	68	36	19
1	2	1	2	1	0	0	0	0

ASL(成功)=(1+2+1+2+1)/9=7/9
失败查找情况分析:
计算出的hash值为9或者10 ,不需要比较即可判断查找失败
如果计算出是0,需要查找0,1,4,三个位置
如果计算出是1,需要查找1,2,5, 三个个个位置
如果计算出是2,需要查找2,3,6 三个位置
… 3,需要查找3,4,7 三个位置
… 4,需要查找 4,5, 两个位置
… 5,需要查找5,6两个位置
… 6 ,需要查找6,7 两个位置
…7 ,需要查找7,8两个位置
…8 ,需要查找8, 一个位置
ASL(失败)=(3+3+4*2+1)/11=15/11
注意:存储数据超过表长一半时,冲突次数大大增加,只要有空间,线性探查总能查找到空间存放数据,二次探测不一定.
伪随机数解决冲突:
取伪随机数为9
最终会发现冲突会更少,分布更均匀.

2.再hash法

将n个不同的hash函数排成一个序列,当发生冲突时,由RHi确定第i次冲突的地址Hi.
Hi=RHi(key) i=1,2,3,…,n
其中:RHi为不同hash函数
这种方法不会产生’聚类’,但是会增加计算时间

3. 连地址法:同一hash值的放在同一个单链表中

java中的hashmap 即是采用此方法
数组+链表的方式
### 4,公共溢出法

哈希表查找:与表构造的方式相同

哈希表插入算法

查找性能分析

哈希表的平均查找长度是装填因子a 的函数,而不是n的函数

总结:

关键字与hash地址一一映射,那么平均查找长度就是0,这是理想化的
但是关键字范围广 $⟶$存储空间范围小
压缩存储
冲突不可避免,不同解决冲突的策略ASL不同,查找表大小与解决冲突策略和ASL范围相关
建立查找表一般流程:
选择hash函数$⟶$根据冲突策略与ASL计算哈希表大小$⟶$建立查找表

---

1. 何时结束块内查找呢?
   如果查到的地址等于下一块内存的首地址,则表示块内查找失败,结束查找 ↩︎