【系列二之图像处理系列】波形处理（3）

1 巴特沃斯滤波器

使用巴特沃斯滤波器进行处理，输入频率范围与阶数，返回值是IIR滤波器的分子b和分母a的多项式系数向量。我们所设定的带通频率在0.5-2HZ之间。又根据采样定理，采样频率要大于两倍的信号本身最大的频率，才能还原信号，所以要归一化截止频率。经过调试发现滤波器阶数是4时效果最好。代码如下所示。

def butter_bandpass(lowcut, highcut, fs, order=4):
    nyq = 0.5 * fs
    low = lowcut / nyq  
    high = highcut / nyq
    b, a = butter(order, [low, high], btype='band')
    return b, a

实现信号滤波，代码如下

def butter_bandpass_filter(data, lowcut, highcut, fs, order=4):
    b, a = butter_bandpass(lowcut, highcut, fs, order=order)
    y=filtfilt(b,a,data)
    return y

2 小波阈值去噪法

小波阈值去噪法又叫阈值收缩法去噪，在非稳定信号的去噪应用中有着良好的效果。采集到的原始信号在小波前会有一定的噪声干扰，原始信号可以看作是信号成分和噪声成分的叠加。原始信号中的噪声在很大程序上类似于高斯白噪声，从小波域来看，原始信号中的有效信号成分对应的系数比例远远大于噪声成分的系数比例，根据高斯分布来看，99.99%的噪声系数应该位于-3σ到3σ的区间内，如果将这部分噪声滤除即可保证在滤除绝大部分噪声的情况下保留尽可能多的有效信号成分。因此，先通过Mallat算法将原始信号多分辨率分解为不同小波系数的分解信号，再将小波系数的模值低于选定阈值的信号去除，最后将经过小波阈值处理的分解信号进行小波重构，即可获得滤波后的信号。小波阈值去噪法的处理流程如下图表示。

2.1几种常见的小波函数

小波变换可分为两种，一种是离散小波变换，另一种是连续小波变换。

2.1.1 Haar小波

Haar小波是滤波分析发展中最先被用到、最简单的一个小波基。它的表达式为：

Haar小波函数图像如下图 所示：

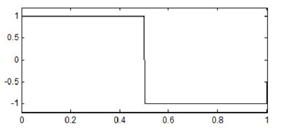
Haar小波变换只需进行加减操作，不需要乘法；输入和输出个数相等；大部分运算为0，计算速度快。因此Haar小波在图片压缩上具有广泛应用，但其在时域上并不连续，故不适合用于平滑函数。

2.1.2 Daubecies小波

法国著名学者I.Daubechies在上世纪90年代研究尺度取2的整次幂的小波变换时构造了Daubecies小波。DbN小波族是双正交小波，并且具有紧支性和N阶消失矩，其主要应用在离散型小波变换，通常使用在数位信号分析、去噪等方面。下图为db4小波的图形。

2.1.3 Coiflets小波

Coiflets小波也是I.Daubechies所设计，并且与db小波一样也是一种离散小波。它波形接近对称，常被用于数字信号处理尤其是影像数据压缩方面。下图为coif1-coif5小波函数。

2.2 Mallat算法

Mallat算法是mallat在研究多分辨率分析理论和图像处理的研究中受到塔式算法的启发提出，实现了离散小波变换的重大突破，极大拓宽了离散小波变换的应用领域。正交小波变换在多分辨率分析中可以看作是信号分别通过一个高通滤波器和低通滤波器的滤波过程，其中高通滤波器输出的是信号分解后的高频分量部分，也被称为细节分量，低通滤波器输出的是信号分解后的低频分量部分，也被称为近似分量，而Mallat算法就是一种小波变换的快速算法。Mallat算法将信号中的高低频部分分隔开来，在保留高频部分信号的同时对低频信号再次分解，低频信号又被分为高频信号和低频信号，更多的层次可以将信号分解为更精细的层次，同时会增加计算量，下图为对原始信号3层分解示意图。

2.2.1 小波变换

心电信号噪声如下表所示。

噪声种类	产生原因	频率范围
工频干扰	电力系数产生的固定干扰	50Hz
肌电干扰	由肌肉颤动所致	5-2000Hz
基线飘移	人体轻微运动等原因 0.005-1Hz

采样信号为240Hz，各尺度近似信号与细节信号的频率带宽如下表所示。

分解尺度	近似信号频率带宽	细节信号频率带宽
1	0-60Hz	60-120Hz
2	0-30Hz	30-60Hz
3	0-15Hz	15-30Hz
4	0-7.5Hz	7.5-15Hz
5	0-3.75Hz	3.75-7.5Hz
6	0-1.875Hz	1.875-3.75Hz
7	0-0.9375Hz	0.9375-1.875Hz

由上表可以看出，当分解尺度为7时，将该尺度上的近似信号置为0，可以去除基线飘移；对于工频干扰，其噪声主要集中在第2层尺度的细节信号；对于肌肉干扰，其噪声主要集中在1-5层尺度的细节信号。

(1)采用多级一维离散小波变换来分解信号，具体代码如下：

coffes = pywt.wavedec(hues0, 'db4',level=7)

其中，hues0为原始信号，选用小波基为db4，分解层级为7，返回值coffes为系数数组(长度为level+1)，系数数组第一个元素为近似(低频)系数数组，系数数组剩余元素均表示细节(高频)系数数组，coffes表示有用信号的小波系数和干扰噪声的小波系数。
注：将信号表示为一系列不同尺度和不同时移的小波函数的线性组合,其中每一项的系数称为小波系数。

(2)使用waverec函数进行小波重构，输入阈值处理后的小波系数、重构小波函数为db4，输出重构之后的信号，代码如下。

wave_array=pywt.waverec(list_coffes, 'db4')

2.3 阈值处理

小波阈值去噪中包含两个重要的影响因素： 阈值的选取方式和阈值函数的选取方式，而滤波的效果也主要由这两个因素决定。
对信号进行小波变换后，信号的小波系数比噪声的小波系数大，所以我们要设置一个门槛来去除噪声。阈值选择的原理基于公式： s(t)=f(t)+e(t)，若s(t)为原始信号中的有效成分，f(t)为信号中的有效成分，e(t)是高斯白噪声N(0,1)。在小波域，有效信号对应的系数很大，而噪声对应的系数很小。噪声在小波域对应的系数仍然满足高斯白噪声分布，因此可以通过小波系数或原始信号来进行评估，并选定在小波域能够消除噪声的阈值。
在应用小波阈值去噪法时，阈值λ的选取至关重要，过大的λ会导致信号中的有效成分被错误滤除，而过小的λ会使滤波后的信号中残留大量噪声。目前常用的阈值选取方法有以下几种：
（1）全局阈值
将统一的阈值应用于整个去噪过程，它的表达式为：

其中，σ代表噪声的标准方差，N代表信号序列的长度。
（2）无偏风险估计阈值
又称为Regsure阈值，由无偏似然估计得出。该方法先提取原始信号s(t)中所有元素的绝对值，再将绝对值序列从小到大排列。最后将所得的有序序列中的所有元素取平方值，得到新的信号序列记为y(k)。表达式为：

设λj为y(k)第j个元素的平方根，即

则有该阈值的风险函数如下式表示：

根据风险函数可以得到对应的风险，曲线，再将风险最小时对应的j值记录为jmin，并由jmin可以得到无偏风险估计阈值：

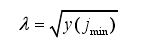
（3）固定阈值
表达式如下：

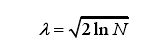
（4）极大极小阈值
它的表达式是：

选取阈值的目的是将分散后的小波系数的模小于阈值的信号滤除，而阈值函数则决定了小波系数大于或等于阈值的信号部分的处理方式，因此阈值函数的选取对于小波阈值法滤波后的信号的连续度和精度都有重要影响。

阈值函数主要可分为两种，分别是硬阈值函数和软阈值函数。

• 硬阈值是将分解后信号的小波系数的绝对值与阈值进行比较，小于阈值的系数为零，大于阈值则保持不变。使用硬阈值函数处理能保留更多的信号边缘局部信息，但它也使得信号具有不连续性，滤波后噪声残留较多，且容易产生波形失真现象。
• 软阈值是将小波系数的绝对值与阈值比较，若系数的绝对值小于阈值则置于零，若大于阈值，则将其设置为该点信号值与阈值的差值，因此对于信号有着方向向着横幅，幅度为阈值的平移作用。相较于硬阈值，软阈值函数处理后的信号拥有更好的连续性，处理后的结果相对平滑，不会产生额外的振荡波形，但软阈值处理本身是一种对信号的压缩行为，这使得软阈值处理后的信号与原始信号存在一定的偏差，这种偏差同样会反映在重构信号中。

使用threshold函数来进行阈值处理，输入要处理的小波系数，阈值及模式，输出为阈值处理后的小波系数，其中阈值选择全局阈值，阈值函数选用软阈值，代码如下所示。

data_soft = pywt.threshold(data=data, value=value, mode='soft')