送外卖问题

有n个小区需要外卖配送，分别有mi（i=0...n-1）个住户需要配送外卖，每户的配送时间均为1小时，现在有w个外卖员，每个外卖员只能送相邻小区，最后配送时间等于配送时间最长的外卖员的配送时间，求最短的配送时间；

最小—最大问题，动态规划

例

有4个小区,每个小区需要配送的住户数：	[5,4,5,3]
有2个外卖配送员
最短配送时间【5,4】，【5,3】	9

 递归地定义最优解

f(k,n):表示k个外卖员，送完n个小区的最短时间，默认参与的外卖员越多，时间越短

最优解为：第k个外卖员送最后{i.....n} n-i个小区的外卖，其他k-1个外卖员送{0....i} i个小区的外卖，能取到的最优解

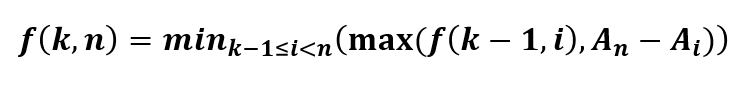
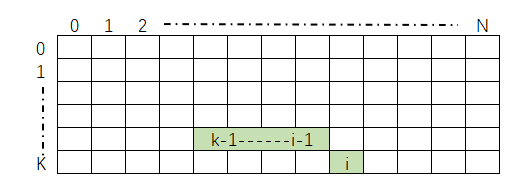
代码
 

import math
def fun(num,data):
    n=len(data)
    sum_data=[sum(data[:i+1]) for i in range(n)]
    # print(sum_data)
    if n<=num:
        return max(data)
    else:
        arr=[[0]*n for _ in range(num)]
        print(arr)
        for j in range(num):
            for i in range(j,n):
                if j==0:
                    arr[j][i]=sum_data[i]
                else:

                    arr[j][i] =min([max(arr[j-1][k],sum_data[i]-sum_data[k]) for k in range(j-1,i)])
        print(arr)
        return arr[-1][-1]
arr=fun(4,[5,4,5,4,6])
print(arr)