算法竞赛入门教程2-分治法

Introduction：

直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。 由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。 分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

关于递归法，这个我们不多说，在于观察规律，举两个简单例子体会一下就好：

1.Fibonacci 

2.Factorial 

3.Hanoi problem

而对于分治法：简言之，就是分而治之，把大问题化简为子问题，走一步，再走一步。我们先说点大话，再仔细实践。

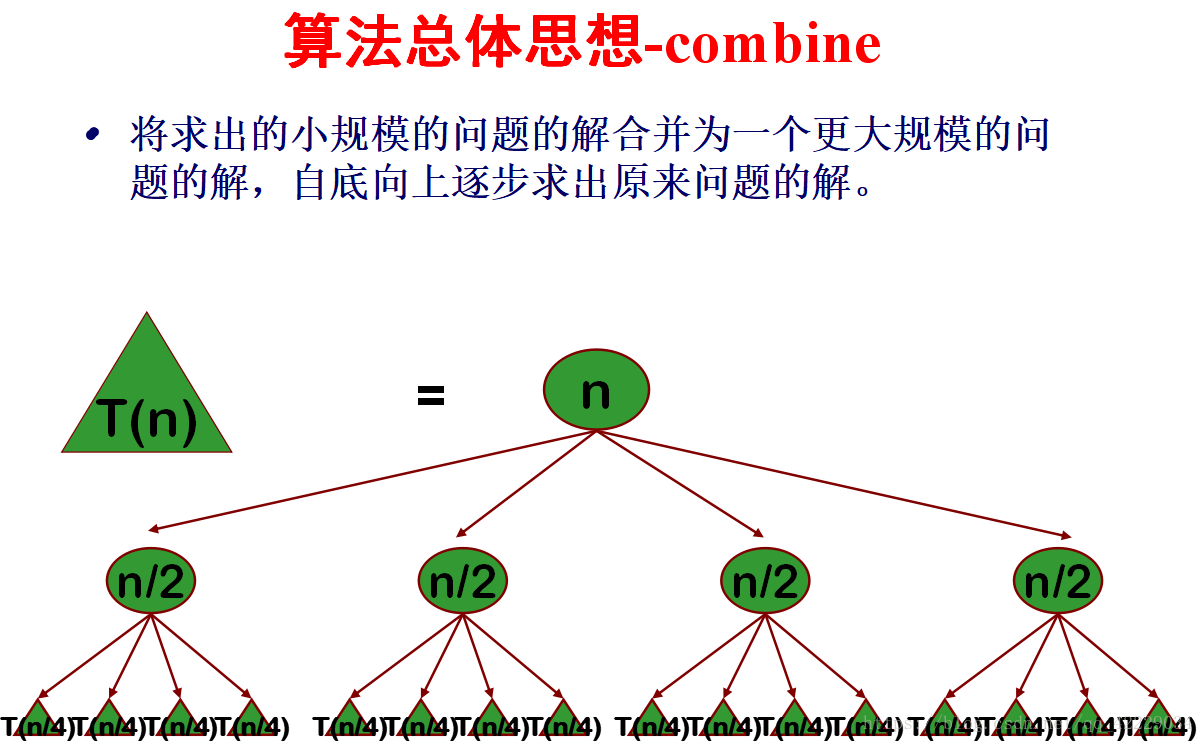
我们举一个生活中的例子，也是我刚想的，超市要根据货物的售出情况分类提供促销方案，这时候我们可能就需要根据货物的情况对货物分类，分别提供促销方案，这时候我们就完成了大问题化小问题的一步。

 

另外根据前辈的研究与调查，总结出了分割原则：在用分治法设计算法时，最好使子问题的规模大致相同。即将一个问题分成大小相等的k个子问题的处理方法是行之有效的。这种使子问题规模大致相等的做法是出自一种平衡(balancing)子问题的思想，它几乎总是比子问题规模不等的做法要好。

分治法所能解决的问题一般具有以下几个特征： 该问题的规模缩小到一定的程度就可以容易地解决； 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质 利用该问题分解出的子问题的解可以合并为该问题的解； 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。 （这条特征涉及到分治法的效率，如果各子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。）

我们举一个最典型的例子-归并排序：

void mergeAdd(int arr[], int left, int mid, int right, int *temp){实现“治”
	int i = left;
	int j = mid + 1;
	int k = left;//临时下标
	while (i <= mid&&j <= right){
		if (arr[i] < arr[j]){
			temp[k++] = arr[i++];
		}
		else{
			temp[k++] = arr[j++];
		}
	}
	while (i <= mid){
		temp[k++] = arr[i++];
	}
	while (j <= right){
		temp[k++] = arr[j++];
	}
	//把temp中的内容拷给arr数组中
	//进行归并的时候，处理的区间是arr[left,right),对应的会把
	//这部分区间的数组填到tmp[left,right)区间上
	memcpy(arr + left, temp + left, sizeof(int)*(right - left+1));
}
void mergeSort(int arr[],int left,int right,int *temp){//实现“分”
	int mid = 0;
	if (left < right){
		mid = left + (right - left) / 2;
		mergeSort(arr, left, mid, temp);
		mergeSort(arr, mid + 1, right, temp);
		mergeAdd(arr, left, mid, right, temp);
	}
	
}
int main(){
	int arr[] = { 8,4,5,7,1,3,6,2};
	int len = sizeof(arr)/sizeof(arr[0]); //提高代码的可移植性
	int *temp = （int*)malloc(sizeof(int)*len);
 
	mergeSort(arr, 0, len - 1, temp);
	free(temp);
	for (int i = 0; i < len; i++){
		printf("%d ", arr[i]);
	}
	system("pause");
	return 0;
}