快速排序算法

1. 思想

快速排序算法是一个采用分治思想的排序算法。其思路如下：

• 第一步：确定分界点。分界点可以是数组的端点，也可以是数组的中间任意一点。假如数组为q，数组左边界为l，有边界为r，我们通常取q[l]、q[r]、q[(l+r)>>2]。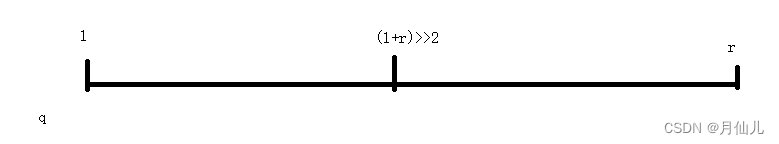

• 第二步：调整区间。让数组左边的元素全部都小于等于分界点的元素，数组右边的元素都大于等于分界点的元素，当然这个左右的分界点不一定是分界点的位置。
  

• 第三步：递归处理数组左右两边。

下面给出关于快速排序的模板：

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i ++; while(q[i] < x);
        do j --; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

我们来分析以下上述算法的时间复杂度。假设程序待处理的规模为$n$，算法循环的时候$i$、$j$一共循环$n$次，而后续的递归划分的区间划分假设以第$k$个元素为分界点。则快速排序所需时间为：

$$T(n)=T(k)+T(n-k-1)+n$$

最好的情况下，每次切分的分界点是$n/2$，则该所需时间为：

$$T(n)=2T(n/2)+n$$

由主定义不难算出最好时候时间复杂度$O(nlogn)$。

接下来看看最坏的时候，假如每次切分的时候总是被划分为$n-1$和$1$这两个区间，则所需时间为：

$$T(n)=T(n-1)+T(1)+n$$

而区间为$1$的时候只需要运算1次，则所需时间表达为:

$$T(n)=T(n-1)+1+n$$

则：

$$\begin{gathered} T(n)=T(n-1)+1+n \\ T(n-1)=T(n-2)+1+n-1 \\ ... \\ T(n-k+1)=T(n-k)+1+n-k+1 \end{gathered}$$

等式左右两边相加，得

$$T(n)=T(n-k)+1\times k+\frac{(n+n-k+1)\times k}{2}$$

当执行$k$次时$T(n-k)=T(1)$，则$k=n-1$，则所需时间可表达为：

$$\begin{array}{rl}T(n)& =T(1)+1\times (n-1)+\frac{(n+n-(n-1)+1)\times (n-1)}{2}\\ & =1+(n-1)+\frac{(n+2)\times (n-1)}{2}\\ & =1+\frac{(n+4)\times (n-1)}{2}\\ & =\frac{n^2}{2}+\frac{3n}{2}-1\end{array}$$

所以不难看出最坏时间复杂度为$O(n^2)$。

2. 例题1 785-快速排序

给定你一个长度为 n的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。

输入格式
输入共两行，第一行包含整数 $n$。
第二行包含 $n$个整数（所有整数均在$1\sim 10^9$范围内），表示整个数列。

输出格式
输出共一行，包含 n个整数，表示排好序的数列。

数据范围
$1\le n\le 100000$

输入样例：
5
3 1 2 4 5

输出样例：
1 2 3 4 5

代码如下：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e6 + 10;
int q[N], n;

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i ++; while(q[i] < x);
        do j --; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++) 
    	scanf("%d", &q[i]);
    quick_sort(q, 0, n - 1);
    for(int i = 0; i < n; i ++) 
    	printf("%d ", q[i]);
    printf("\n");
    return 0;
}

3. 例题2 786-第k个数

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k个数。

输入格式
第一行包含两个整数 $n$和 $k$。
第二行包含$n$个整数（所有整数均在 $1\sim 10^9$范围内），表示整数数列。

输出格式
输出一个整数，表示数列的第 $k$小数。

数据范围
$1\le n\le 100000,1\le k\le n$

输入样例：
5 3
2 4 1 5 3

输出样例：
3

代码如下：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1e6 + 10;
int q[N], n, k;

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i ++; while(q[i] < x);
        do j --; while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
    
}

int main()
{
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n; i ++) 
        scanf("%d", &q[i]);
    quick_sort(q, 0, n - 1);
    printf("%d\n", q[k - 1]);
    return 0;
}