拓扑排序

最新推荐文章于 2025-06-30 13:40:45 发布

diyhoos

最新推荐文章于 2025-06-30 13:40:45 发布

阅读量282

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构文章标签：排序

本文链接：https://blog.youkuaiyun.com/qq_42020563/article/details/80547170

数据结构专栏收录该内容

19 篇文章

订阅专栏

拓扑排序是对有向无环图（DAG）的顶点进行排序，使得若图中从V到W存在有向路径，则V总是在W之前。在拓扑排序过程中，每次输出入度为0的顶点。此外，拓扑排序还应用于解决关键路径问题，例如在项目工序安排中的AOE网络分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足此条件的顶点序列称为一个拓扑序。获得一个拓扑序的过程就是拓扑排序。AOV如果有合理的拓扑序，则必定是有向无环图（Directed Acyclic Graph，DAG）

每次输出没有前驱顶点的课程。即输出入度为0的顶点。

void TopSort()
{   for(cnt=0;cnt<|V|;cnt++)
      { V=未输出的入度为0的顶点；
        if(这样的点不存在）
          {cout<<"图中有回路”；
             break;
           }
        输出v，或者记录V的输出编号；
        for(V的每个邻接点w）
         Indegree[w]--;
       }
}

随时将入度为0的顶点放入一个容器中

void TopSort()
{  for(图中每个顶点)
      if(Indegree[V]==0)
         Enqueue(V,Q);
      while(!IsEmpty(Q))
       {   V=Dequeue(Q);
            输出V，cnt++；
           for(V的每个邻接点w）
              if(--Indegree[W]==0)
                   Enqueue(W,Q);
         }
    if(cnt!=|V|)
       cout<<"图中有回路";
}

关键路径问题

AOE（Activity On Edge）网络

一般用于安排项目的工序

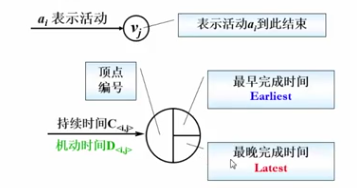
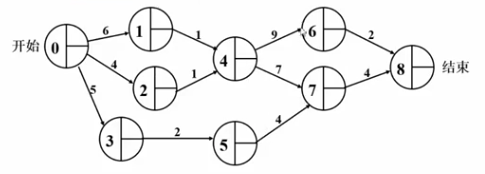
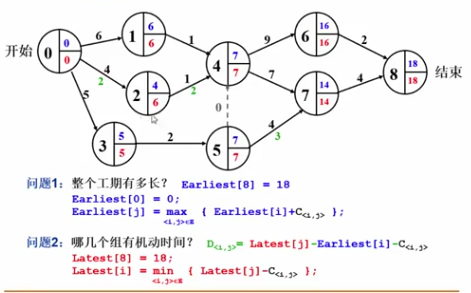
D<I,J>=Latest[j]-Earliest[i]-C<i,j>//机动时间

关键路径：由绝对不允许延误的活动组成的路径，如将关键路径加快进度，则整个项目就能提前完工。