问题描述
矩阵的相似变换不改变矩阵的特征值,根据这一原理,我们可以利用一系列的特殊相似变换把原矩阵 A A A进行变,使之易求特征值。
算法思想
任意实对称矩阵
A
A
A总可以通过正交相似变换为对角形。因此寻找正交矩阵
R
R
R,使得
R
T
A
R
=
d
i
a
g
(
λ
i
)
{R^T}AR = diag({\lambda _i})
RTAR=diag(λi),实对称矩阵
A
A
A的特征值就是对角阵
d
i
a
g
(
λ
i
)
diag({\lambda _i})
diag(λi)的对角线元素。
R
R
R的各列就是对应的特征向量。
J
a
c
o
b
i
Jacobi
Jacobi提出一系列平面旋转矩阵来构造矩阵
R
R
R。在正交相似的变换下,矩阵元素的平方和保持不变。因此寻找这种变换,使得非对角元素接近于
0
0
0,对角元素取极大值,这就是
J
a
c
o
b
i
Jacobi
Jacobi算法的思想。
设
A
A
A是实对称矩阵,取
A
0
=
A
{A_0} = A
A0=A,按照下面格式形成一个相似矩阵序列:
A
k
=
R
k
A
k
−
1
R
k
T
,
k
=
1
,
2
⋯
{{A_k} = {R_k}{A_{k - 1}}R_k^T},{k = 1,2 \cdots }
Ak=RkAk−1RkT,k=1,2⋯
若
A
k
−
1
{A_{k - 1}}
Ak−1的非对角线元素中按模最大的元素是
a
p
q
,
p
<
q
{a_{pq}},p<q
apq,p<q取
R
k
{R_k}
Rk具有如下形状:
[
1
⋱
cos
θ
sin
θ
1
⋱
1
−
sin
θ
cos
θ
⋱
1
]
\begin{bmatrix} 1&{}&{}&{}&{}&{}&{}&{}&{}\\ {}& \ddots &{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{\cos \theta }&{}&{}&{}&{\sin \theta }&{}&{}\\ {}&{}&{}&1&{}&{}&{}&{}&{}\\ {}&{}&{}&{}& \ddots &{}&{}&{}&{}\\ {}&{}&{}&{}&{}&1&{}&{}&{}\\ {}&{}&{ - \sin \theta }&{}&{}&{}&{\cos \theta }&{}&{}\\ {}&{}&{}&{}&{}&{}&{}& \ddots &{}\\ {}&{}&{}&{}&{}&{}&{}&{}&1 \end{bmatrix}
⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1⋱cosθ−sinθ1⋱1sinθcosθ⋱1⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
由
A
k
−
1
{{\rm{A}}_{k - 1}}
Ak−1到
A
k
{{\rm{A}}_{k }}
Ak ,只有
A
k
−
1
{{\rm{A}}_{k - 1}}
Ak−1的
p
p
p行
p
p
p列,
q
q
q行
q
q
q列元素发生变化,其它元素保持不变,则:
a
i
j
(
k
)
=
a
i
j
(
k
−
1
)
,
i
,
j
=
1
,
2
,
⋯
n
;
i
,
j
≠
p
,
q
.
{a_{ij}^{(k)} = a_{ij}^{(k - 1)}},{i,j = 1,2, \cdots n;i,j \ne p,q.}
aij(k)=aij(k−1),i,j=1,2,⋯n;i,j=p,q.
而
A
k
{{\rm{A}}_{k }}
Ak的
p
,
p
p,p
p,p列元素是:
{
a
i
p
(
k
)
=
a
p
i
(
k
)
=
a
i
p
(
k
−
1
)
cos
θ
+
a
i
q
(
k
−
1
)
sin
θ
a
i
q
(
k
)
=
a
q
i
(
k
)
=
−
a
i
p
(
k
−
1
)
sin
θ
+
a
i
q
(
k
−
1
)
cos
θ
a
p
q
(
k
)
=
a
q
p
(
k
)
=
(
a
q
q
(
k
−
1
)
−
a
p
p
(
k
−
1
)
)
sin
θ
cos
θ
+
a
p
q
(
k
−
1
)
(
cos
2
θ
+
sin
2
θ
)
a
p
p
(
k
)
=
a
p
p
(
k
−
1
)
cos
2
θ
+
2
a
p
q
(
k
−
1
)
sin
θ
cos
θ
+
a
q
q
(
k
−
1
)
sin
2
θ
a
q
q
(
k
)
=
a
p
p
(
k
−
1
)
sin
2
θ
+
2
a
p
q
(
k
−
1
)
sin
θ
cos
θ
+
a
q
q
(
k
−
1
)
cos
2
θ
\begin{cases} {a_{ip}^{(k)} = a_{pi}^{(k)} = a_{ip}^{(k - 1)}\cos \theta + a_{iq}^{(k - 1)}\sin \theta }\\ {a_{iq}^{(k)} = a_{qi}^{(k)} = - a_{ip}^{(k - 1)}\sin \theta + a_{iq}^{(k - 1)}\cos \theta }\\ {a_{pq}^{(k)} = a_{qp}^{(k)} = (a_{qq}^{(k - 1)} - a_{pp}^{(k - 1)})\sin \theta \cos \theta + a_{pq}^{(k - 1)}({{\cos }^2}\theta + {{\sin }^2}\theta )}\\ {a_{pp}^{(k)} = a_{pp}^{(k - 1)}{{\cos }^2}\theta + 2a_{pq}^{(k - 1)}\sin \theta \cos \theta + a_{qq}^{(k - 1)}{{\sin }^2}\theta }\\ {a_{qq}^{(k)} = a_{pp}^{(k - 1)}{{\sin }^2}\theta + 2a_{pq}^{(k - 1)}\sin \theta \cos \theta + a_{qq}^{(k - 1)}{{\cos }^2}\theta } \end{cases}
⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧aip(k)=api(k)=aip(k−1)cosθ+aiq(k−1)sinθaiq(k)=aqi(k)=−aip(k−1)sinθ+aiq(k−1)cosθapq(k)=aqp(k)=(aqq(k−1)−app(k−1))sinθcosθ+apq(k−1)(cos2θ+sin2θ)app(k)=app(k−1)cos2θ+2apq(k−1)sinθcosθ+aqq(k−1)sin2θaqq(k)=app(k−1)sin2θ+2apq(k−1)sinθcosθ+aqq(k−1)cos2θ
选择
R
k
{R_k}
Rk使得元素
a
p
q
(
k
=
0
a_{pq}^{(k} = 0
apq(k=0,这时
θ
\theta
θ应满足:
tan
θ
=
2
a
p
q
(
k
−
1
)
a
p
p
(
k
−
1
)
−
a
q
q
(
k
−
1
)
\tan \theta = \frac{{2a_{pq}^{(k - 1)}}}{{a_{pp}^{(k - 1)} - a_{qq}^{(k - 1)}}}
tanθ=app(k−1)−aqq(k−1)2apq(k−1)
通常将
2
θ
2\theta
2θ限制在主值范围之内,即
−
π
4
≤
θ
≤
π
4
-\frac {\pi }{4}\le\theta\le\frac{\pi }{4}
−4π≤θ≤4π
若
a
p
p
(
k
−
1
)
−
a
q
q
(
k
−
1
)
=
0
a_{pp}^{(k - 1)} - a_{qq}^{(k - 1)} = 0
app(k−1)−aqq(k−1)=0时,取
θ
=
s
g
n
(
a
p
q
(
k
−
1
)
)
π
4
\theta = {\mathop{\rm sgn}} (a_{pq}^{(k - 1)})\frac{\pi }{4}
θ=sgn(apq(k−1))4π
令
{
y
=
∣
a
p
p
(
k
−
1
)
−
a
q
q
(
k
−
1
)
∣
x
=
s
g
n
(
a
p
p
(
k
−
1
)
−
a
q
q
(
k
−
1
)
)
⋅
2
a
p
q
(
k
−
1
)
\begin{cases} {y = \left| {a_{pp}^{(k - 1)} - a_{qq}^{(k - 1)}} \right|}\\ {x = {\mathop{\rm sgn}} (a_{pp}^{(k - 1)} - a_{qq}^{(k - 1)}) \cdot 2a_{pq}^{(k - 1)}} \end{cases}
{y=∣∣∣app(k−1)−aqq(k−1)∣∣∣x=sgn(app(k−1)−aqq(k−1))⋅2apq(k−1)
因此
{
cos
2
θ
=
1
2
(
1
+
y
x
2
+
y
2
)
sin
2
θ
=
1
2
x
x
2
+
y
2
1
cos
θ
\begin{cases} {{{\cos }^2}\theta = \frac{1}{2}(1 + \frac{y}{{\sqrt {{x^2} + {y^2}} }})}\\ {{{\sin }^2}\theta = \frac{1}{2}\frac{x}{{\sqrt {{x^2} + {y^2}} }}\frac{1}{{\cos \theta }}} \end{cases}
⎩⎨⎧cos2θ=21(1+x2+y2y)sin2θ=21x2+y2xcosθ1
由于
A
k
{A_k}
Ak的对称性,实际计算时只需对
A
k
{A_k}
Ak的上三角(下三角)元素进行即可,这样减少了工作量,又保证了
A
k
{A_k}
Ak的严格对称性。
测试数据
[ 1 0 2 0 2 1 2 1 1 ] \begin{bmatrix} 1&0&2\\ 0&2&1\\ 2&1&1 \end{bmatrix} ⎣⎡102021211⎦⎤
C语言程序
#include <stdio.h>
#include <stdlib.h>
#include<math.h>
#define MaxSize 100
#define error 1e-6
double A[MaxSize][MaxSize];
double A0[MaxSize][MaxSize];
double A1[MaxSize][MaxSize];
double R1[MaxSize][MaxSize];
double R2[MaxSize][MaxSize];//R1的转置
int n;
void input()
{
int i,j;
printf("请输入矩阵A的行数:\n");
scanf("%d",&n);
printf("请输入矩阵A:\n");
for(i=0;i<n;i++)
for(j=0;j<n;j++)
scanf("%lf",&A[i][j]);
}
void Jacobi()
{
int i,j,k,r;
double seta;
for(k=1;k<100;k++)
{
int p,q;
for(i=0;i<n;i++)//算法第一步,把A赋值给A0
for(j=0;j<n;j++)
A0[i][j]=A[i][j];
//double max1=fabs(A0[0][1]);
double max1=0;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{//寻找除主元素外的最大值
if(i!=j)
{
if(max1<fabs(A0[i][j]))//必须用fabs对浮点型求绝对值
{
max1=A0[i][j];
p=i;//记录最大元素下标
q=j;
}
}
}
//计算seta值
seta=0.5*(atan(2*A0[p][q]/(A0[p][p]-A0[q][q])));
printf("第%d次tan的结果%lf:\n",k,tan(seta));
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{//R1(k),R2(k)赋值
if(i==j)
{
R1[i][j]=1;
R2[i][j]=1;
}
else
{
R1[i][j]=0;
R2[i][j]=0;
}
}
R1[p][p]=cos(seta);
R1[p][q]=sin(seta);
R1[q][p]=-sin(seta);
R1[q][q]=cos(seta);
R2[p][p]=cos(seta);
R2[p][q]=-sin(seta);
R2[q][p]=sin(seta);
R2[q][q]=cos(seta);
double Z[MaxSize][MaxSize];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
double sum=0;
for(r=0;r<n;r++)
{
sum=sum+R1[i][r]*A0[r][j];
}
Z[i][j]=sum;//算法第一步,把A赋值给A0m;
}
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
double sum1=0;
for(r=0;r<n;r++)
{
sum1=sum1+Z[i][r]*R2[r][j];
}
A[i][j]=sum1;
}
printf("第%d,%d次R的结果:\n",p+1,q+1);
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
printf("%lf ",R1[i][j]);
printf("\n");
}
printf("第%d次A的结果:\n",k+1);
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
printf("%lf ",A[i][j]);
printf("\n");
}
int flag=0;//判断是否满足精度
for(i=0;i<n;i++)
{
if(fabs(A[i][i]-A0[i][i])<error)
flag++;
}
if(flag==n)
break;
}
}
int main()
{
void input();
void Jacobi();
input();
Jacobi();
return 0;
}
实验结果
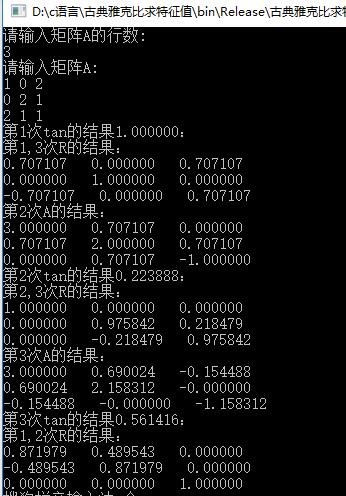
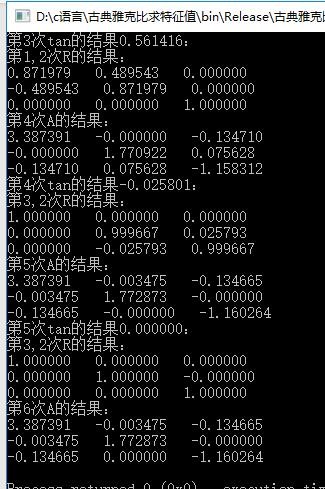

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








