逻辑回归----线性逻辑回归与非线性逻辑回归

线性逻辑回归

逻辑回归的预测函数

逻辑回归的代价函数

如果采用线性回归的代价函数的形式，随着自变量$\theta$的变化将会出现很多的局部最小值（如下图左边所示），不适合使用梯度下降法求解参数。
所以采用了如下代价函数：

所以，合并后的损失函数如下：

利用梯度下降法更新参数如下：

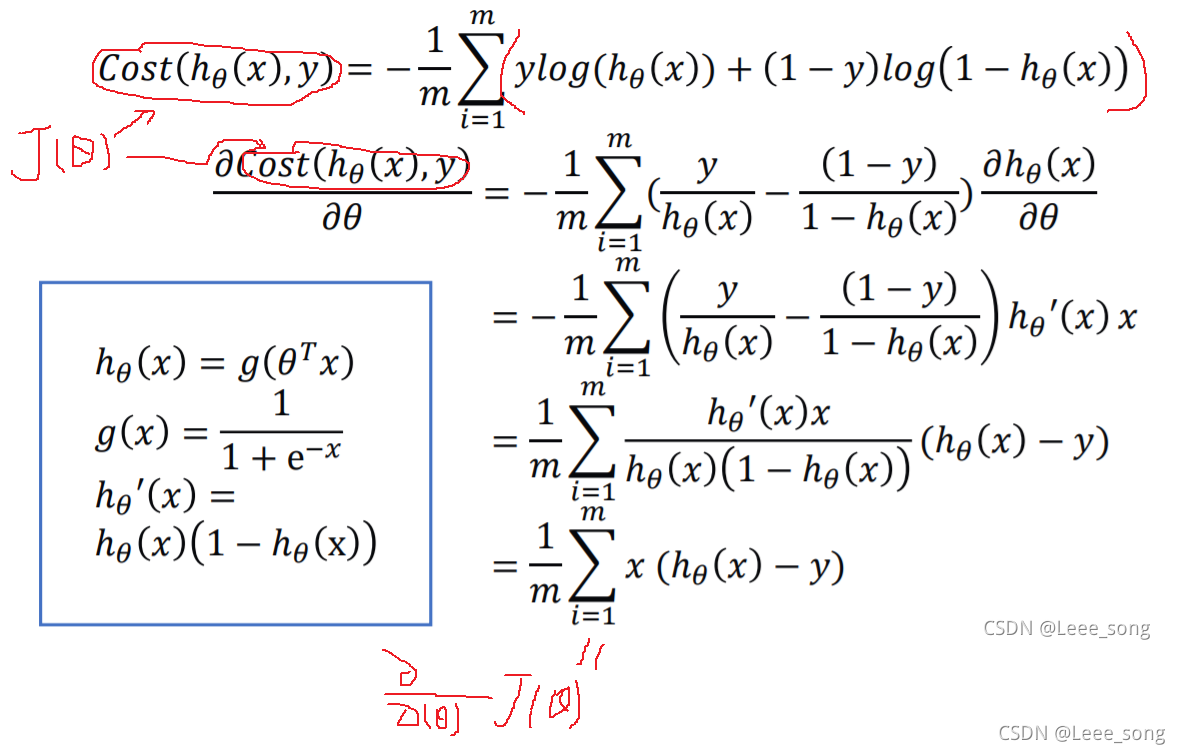
逻辑回归正则化：

python梯度下降法实现逻辑线性回归：

import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import classification_report
from sklearn import preprocessing

# 数据是否需要标准化
scale = False

# 载入数据
data = np.genfromtxt("LR-testSet.csv", delimiter=",")
x_data = data[:,:-1]# x_data含有两列，表示两个特征（这里表示坐标）
y_data = data[:,-1,np.newaxis]# y_data含有一列，表示一个结果
    
# 定义绘图函数
def plot():
    x0 = []
    x1 = []
    y0 = []
    y1 = []
    # 切分不同类别的数据
    for i in range(len(x_data)):
        if y_data[i]==0:# 是类别0则将他的两个特征分别加入x0,y0,这里的两个特征其实就是坐标
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:# 是类别1则将他的两个特征分别加入x1,y1
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])

    # 画图
    scatter0 = plt.scatter(x0, y0, c='b', marker='o')
    scatter1 = plt.scatter(x1, y1, c='r', marker='x')
    #画图例
    plt.legend(handles=[scatter0,scatter1],labels=['label0','label1'],loc='best')
   


# 给样本添加偏置项,添加一列1到第0列
X_data = np.concatenate((np.ones((100,1)),x_data),axis=1)


def sigmoid(x):#定义分类函数。可以传入一个(1,n)的矩阵，得到一个(1,n)的结果
    return 1.0/(1+np.exp(-x))


# 代价函数
def cost(xMat, yMat, ws):
    left = np.multiply(yMat, np.log(sigmoid(xMat*ws)))# (m,1)*((m,n)*(n,1))=(m,1)对于矩阵，*是矩阵相乘，multiply是对应位置相乘
    right = np.multiply(1 - yMat, np.log(1 - sigmoid(xMat*ws)))
    return np.sum(left + right) / -(len(xMat))# 将每一组的损失加起来求平均表示当前的平均损失 


# 梯度下降法，需要接受一个带有偏置的特征二维数组xArr和结果标签二维数组yArr
def gradAscent(xArr, yArr):
    if scale == True:
        xArr = preprocessing.scale(xArr) #数据集的标准化
       
    # 将数组转为矩阵方便下面矩阵计算
    xMat = np.mat(xArr)
    yMat = np.mat(yArr)

    #学习率和训练次数
    lr = 0.001