排序算法-手撕代码

目录

1、冒泡排序：

2、插入排序

3、原始希尔排序

4、有序子列的归并

5、递归算法

6、非递归算法

7、快速排序

8、基数排序

9、各个排序算法的比较

10、二分查找法

---

1、冒泡排序：

void Bubble_Sort(ElementType A[], int N)
{
    for(p = N-1; p >= 0; p--)
    {
        flag = 0;
        for(i = 0; i < p; i++)
        {
            if(A[i] > A[i+1])
            {
                swap(A[i], A[i+1]);
                flag = 1;
            }
        }
        if(flag == 0) break;
    }
}

2、插入排序

void Insert_Sort(ElementType A[], int N)
{
    for(p = 1; p < N; p++)
    {
        tmp = A[p];
        for(i = p; i > 0 && A[i-1] > tmp; i--)
        {
            A[i] = A[i-1];
        }
        A[i] = tmp;
    }
}

3、原始希尔排序

void Shell_Sort(ElementType A[], int N)
{
    for(D = N/2; D > 0 ; D /= 2)
    {
        for(p = D; p < N; p++)
        {
            tmp = A[p];
            for(i = p; i >= D && A[i-D] > tmp; i -= D)
                A[i] = A[i-D];
            A[i] = tmp;
        }
    }
}

4、有序子列的归并

void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd)
{
    LeftEnd = R - 1;
    Tmp = L;
    NumElements = RightEnd - L + 1;
    while(L <= LeftEnd && R <= RightEnd)
    {
        if(A[L] <= A[R]) TmpA[Tmp++] = A[L++];
        else             TmpA[Tmp++] = A[R++];
    }
    while(L <= LeftEnd)
        TmpA[Tmp++] = A[L++];
    while(R <= RightEnd)
        TmpA[Tmp++] = A[R++];
    for(i = 0; i < NumElements; i++, RightEnd--)
        A[RightEnd] = TmpA[RightEnd];
}

5、递归算法

void MSort(ElementType A[], ElementType TmpA[], int L, int RightEnd)
{
    int Center;
    if(L < RightEnd)
    {
        Center = (L + RightEnd) / 2;
        MSort(A, TmpA, L, Center);
        MSort(A, TmpA, Center+1, RightEnd);
        Merge(A, TmpA, L, Center+1, RightEnd);
    }
}
​
void Merge_Sort(ElementType A[], int N)
{
    ElementType *TmpA;
    TmpA = malloc(N * sizeof(ElementType));
    if(Tmp != NULL)
    {
        MSort(A, TmpA, 0, N-1);
        free(TmpA);
    }
    else Error("空间不足");
}

6、非递归算法

void Merge_Pass(ElementType A[], ElementType TmpA[], int N, int length)
{
    for(i = 0; i <= N-2*length; i += 2*length)
        Merge1(A, TmpA, i, i+length, i+2*length-1);
    if(i+length < N)
        Merge1(A, TmpA, i, i+length, N-1);
    else
        for(j = i; j < N; j++) TmpA[j] = A[j];
}
​
void Merge_Sort(ElementType A[], int N)
{
    int length = 1;
    TmpA = malloc(N * sizeof(ElementType));
    if(TmpA != NULL)
    {
        while(length < N)
        {
            Merge_Pass(A, TmpA, N, length);
            length *= 2;
            Merge_Pass(TmpA, A, N, length);
            length *= 2;
        }
        free(TmpA);
    }
    else Error("空间不足");
}

7、快速排序

void QuickSort(ElementType A[], int Left, int Right)
{
    if(Cutoff <= Right-Left)
    {
        Pivot = Median3(A, Left, Right);
        i = Left; j = Right - 1;
        for(;;)
        {
            while(A[++i] < Pivot) {}
            while(A[--j] > Pivot) {}
            if(i < j)
                Swap(&A[i], &A[j]);
            else break;
        }
        Swap(&A[i], &A[Right-1]);
        QuickSort(A, Left, i-1);
        QuickSort(A, i+1, Rihjt);
    }
    else
        Insertion_Sort(A+Left, Right-Left+1);
}
​
void Quick_Sort(ElementType A[], int N)
{
    QuickSort(A, 0, N-1);
}

8、基数排序

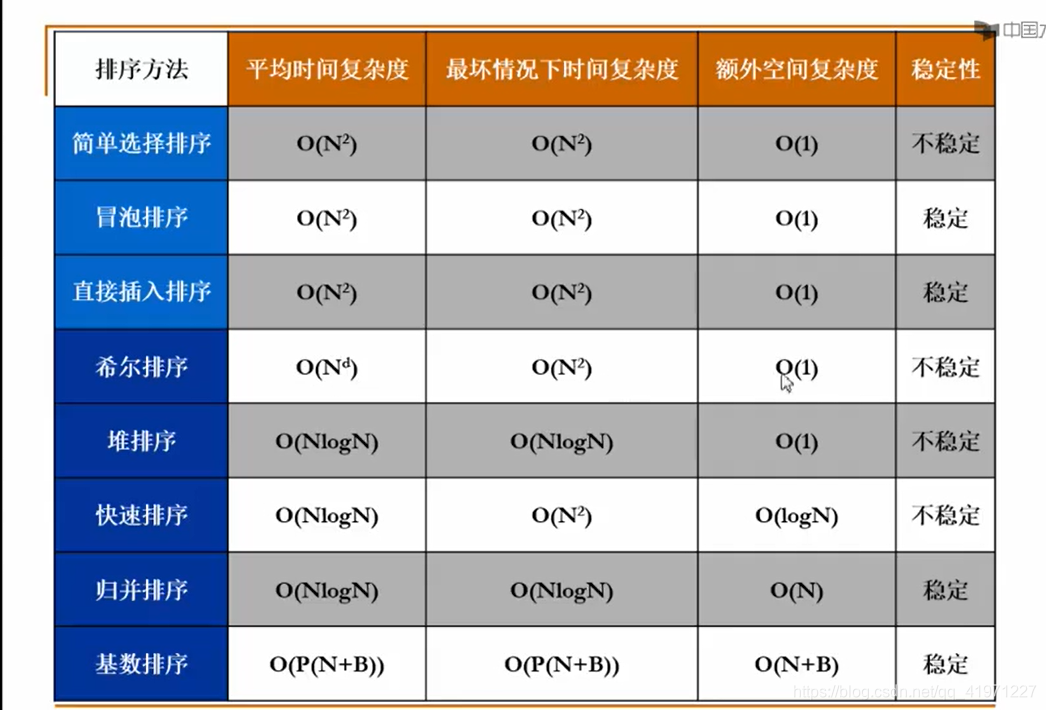
9、各个排序算法的比较

10、二分查找法

int binSearch(int key,int length, int array[])
{
    int mid=0;
    int start = 0;
    int end = length - 1;
    while (start <= end)
    {
        mid = (end - start) / 2 + start;
        if (key == array[mid])
        {
            return mid;
        }
        if (key < array[mid])
        {
            end = mid - 1;
        }
        else if (key > array[mid])
        {
            start = mid + 1;
        }
        else
        {
            return mid;
        }
    }
    return -1;
}