递归程序设计

最新推荐文章于 2022-10-04 22:26:40 发布

原创最新推荐文章于 2022-10-04 22:26:40 发布 · 507 阅读

1 ·

CC 4.0 BY-SA版权

博客围绕用递归和非递归方法解决两个问题展开。一是计算赶鸭卖鸭问题，给出递归和非递归算法；二是角谷定理问题，介绍递归出口和表达式。同时强调使用递归时要设定好递归出口，否则会出现栈溢出错误。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目分析
用递归方法设计下列各题，并给出每道题目的递归出口（递归结束的条件）和递归表达式。同时考虑题目可否设计为非递归方法，如果可以，设计出非递归的算法。
1.一个人赶着鸭子去每个村庄卖，每经过一个村子卖去所赶鸭子的一半又一只。这样他经过了七个村子后还剩两只鸭子，问他出发时共赶多少只鸭子？经过每个村子卖出多少只鸭子？
2.角谷定理。输入一个自然数，若为偶数，则把它除以2，若为奇数，则把它乘以3加1。经过如此有限次运算后，总可以得到自然数值1。求经过多少次可得到自然数1。
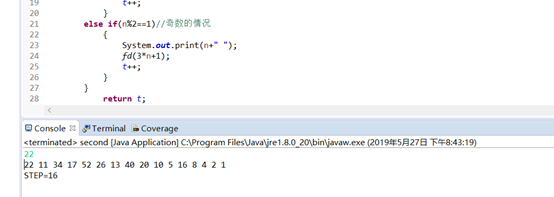
如：输入22，
输出 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1
STEP=16
算法构造
第一题：
这个题运用相关的数学表达式推导即可得到相应的递归表达式
设n为鸭子数；
则：n-(n/2+1)=剩余鸭子数;
则：n=2*(剩余鸭子数+1)
在递归函数体中，剩余鸭子数也要使用n表示，即为：
n=2*(n+1)
设s为每次经过相应的村子卖出的鸭子数，则有：
s=(n/2)+1;

递归出口：
i==0
递归表达式：
当i大于0时进行下列函数体中的操作
n=2(n+1);//第一个n是经过此村子之前的鸭子数，后一个n是经过此村子之后的鸭子数（即剩余数）
s=n/2+1; //s是经过这个村子是卖出的鸭子数量
i–;//i是函数体变量*

对于非递归，只需要用两个变量a,b分别记录进村子前的鸭子数和进入村子之后的鸭子数即可，相应的主要函数体如下：（其中j是村子数量，由函数的参数传入）
for(int i=j;i>0;i–)
{
b=2*(a+1);
s=b/2+1;
a=b;
System.out.println(“在第”+i+“个村子卖出”+s+“个鸭子”);
}

第二题：
递归：
递归出口：

n==1

递归表达式：

			if(n%2==0)//偶数的情况
			{
				System.out.print(n+" ");
				fd(n/2);
				t++;
			}
		else if(n%2==1)//奇数的情况
			{
				System.out.print(n+" ");
				fd(3*n+1);
				t++;
			}
非递归：
public static int f(int n)
	{
		int t=1;
		while(n!=1)
		{
			if((n&1)==0)//偶数
			{
				System.out.print(n+" ");
				n/=2;
				t++;
			}
			else//奇数
			{
				System.out.print(n+" ");
				n=3*n+1;
				t++;
			}
		}
		System.out.println(n);
		return t;
	}

算法实现
第一题：

package shangji;
import java.util.*;
public class first{
   static int c=0; //设置鸭子总数为全局静态变量
   public static int fd(int i,int n)//i是村子总数，n是目前剩余的鸭子总数(递归)
   {
   	int sum=n;
   	int s=0;//s为来到当前村子卖出的鸭子数;
   	if(0==i)//经过第一个村子前
   	{
   		System.out.println("一开始鸭子总数为："+n+"只");
   		c=n;
   	}
   	if(i>0)
   	{
   		n=2*(n+1);//第一个n是经过此村子之前的鸭子数，后一个n是经过此村子之后的鸭子数
   		s=n/2+1;
   		i--;
   		fd(i,n);
   		System.out.println("经过第"+(i+1)+"个村子卖出"+s+"个鸭子");
   	}
   	
   	return c;
   }
   public static int f(int j,int n)//非递归
   {
   	int a=n;//当前剩余鸭子数
   	int b=0;//经过此村子前的鸭子总数
   	int s=0;//在当前村子卖出的鸭子数量
   	for(int i=j;i>0;i--)
   	{
   		b=2*(a+1);
   		s=b/2+1;
   		a=b;
   		System.out.println("在第"+i+"个村子卖出"+s+"个鸭子");
   	}
   	System.out.println("一开始鸭子总数为："+a+"只");
   	c=a;
   	return c;
   }
   public static void test(int sum,int t)//测试类，传入相关鸭子总数sum和村子总数t进行测试
   {
   	for(int i=0;i<t;i++)
   	{
   		sum-=(sum/2+1);
   	}
   	if(sum==2)
   		System.out.println("测试成功，运行无误，最后剩余"+sum+"个鸭子");
   	else
   	{
   		System.out.println("测试失败");
   	}
   }
   public static void main(String args[])
   {
   	int sum;
   	first f0=new first();//声明相关的对象
   	sum=f0.f(7, 2);//调用递归的程序
   	//sum=f0.fd(7, 2);//调用非递归的程序
   	test(sum,7);
   }
}

第二题：

package shangji;
import java.util.*;
public class second 
{
	static int t=0;//设置次数为全局变量
	public static int fd(int n)
	{
		if(n==1)//递归出口
		{
			System.out.println(n);
			t++;
		}
		else
		{
			if(n%2==0)//偶数的情况
			{
				System.out.print(n+" ");
				fd(n/2);
				t++;
			}
		else if(n%2==1)//奇数的情况
			{
				System.out.print(n+" ");
				fd(3*n+1);
				t++;
			}
		}
			return t;
		
	}
	public static int f(int n)
	{
		int t=1;
		while(n!=1)
		{
			if((n&1)==0)//偶数
			{
				System.out.print(n+" ");
				n/=2;
				t++;
			}
			else//奇数
			{
				System.out.print(n+" ");
				n=3*n+1;
				t++;
			}
		}
		System.out.println(n);
		return t;
	}
	public static void main(String args[])
	{
		int n;
		Scanner in=new Scanner(System.in);
		n=in.nextInt();
		int t=f(n);
		System.out.println("STEP="+t);
	}
	
}

运行结果
第一题：
测试代码：

public static void test(int sum,int t)//传入相关鸭子总数sum和村子总数t进行测试
	{
		for(int i=0;i<t;i++)
		{
			sum-=(sum/2+1);
		}
		if(sum==2)
			System.out.println("测试成功，运行无误，最后剩余"+sum+"个鸭子");
		else
		{
			System.out.println("测试失败");
		}
	}

在主函数中传入相关参数调用测试方法即可；

测试及运行截图如下：
递归：
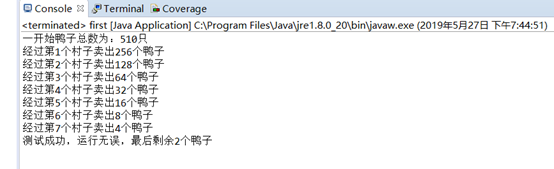
在这里插入图片描述

非递归：

在这里插入图片描述
第二题：

运行截图:
在这里插入图片描述

经验归纳
此次的上机作业是用递归解决两个实际问题，在使用递归来解决问题时，需要注意的地方就是递归出口的设定，一开始在做的时候，由于相关的递归出口没有设定好，导致出现了：java.lang.StackOverflowError递归的栈溢出错误，对此得知，递归不能无限调用自身而不退出递归结构。因此，在写递归算法时，需要设定好相关的退出条件来退出递归循环结构。