关于codeforces的 Vasya and Robot的题解

最新推荐文章于 2020-02-16 14:59:44 发布

原创最新推荐文章于 2020-02-16 14:59:44 发布 · 370 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#codeforces

ACM 专栏收录该内容

6 篇文章

订阅专栏

本文详细解析了CodeForces上Vasya and Robot问题的解决方案，通过前缀和方法记录移动距离，利用二分查找确定改变序列区间的最小长度，以匹配指定终点。

关于codeforces的 Vasya and Robot的题解

题目描述
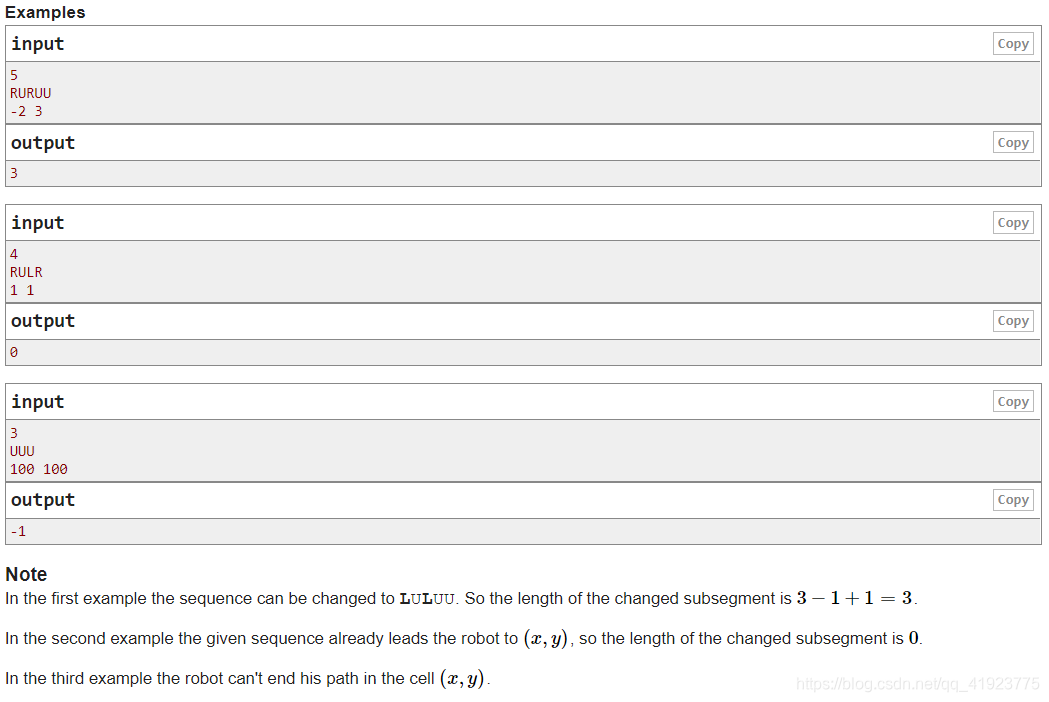
分析
题目给定一段序列包含字母UDLR分别表示上下左右四个方向，按照这个序列可以走到一个实际的的终点，同时题目给定一个终点，需要去改变序列中的一段区间使得实际的终点就是给定的终点，求这个区间的最小长度。
方法
（1）利用类似前缀和的方法将当前x和y移动的距离记录下来
（2）假定对于给定区间[l,r]，那么这段区间原来走的顺序对于x的影响为 x[n] - (x[ r -1 ] - x[ l - 1 ])
（3）计算出如果没有这段区间的x和y方向的位置，并计算出此时和目标位置的差值，此时需要满足两个条件，x方向到目标点的距离和y方向到目标点的距离之和一定要小于等于这段区间的长度，如果是小于那么还存在多余的行走顺序，此时要保证多余的长度可以被2整除，否则也无法到达目标点
（4）利用二分的方法不断地寻找这个最短的区间
code：

#include <iostream>
#include <string>
#include <cmath>
using namespace std;
int x[200000],y[200000];
int a,b,n;
int check(int m){
    for(int i=1;i<=n-m+1;i++){
        int tx=x[n]-x[i+m-1]+x[i-1];  
        int ty=y[n]-y[i+m-1]+y[i-1];  
        int ex=a-tx, ey=b-ty;       
        if(m>=(abs(ex)+abs(ey)) && (m-abs(ex)-abs(ey))%2==0){
        	return 1;
		}
    }
    return 0;
}
int main(){
    string s;
    while(cin>>n){
       	cin>>s;
       	cin>>a>>b; 
        x[0]=y[0]=0;
        for(int i=0;i<n;i++){
            x[i+1]=x[i];y[i+1]=y[i];  
            if(s[i]=='L'){
            	x[i+1]--; 
			}
            else if(s[i]=='R'){
            	x[i+1]++;
			} 
            else if(s[i]=='D'){
            	y[i+1]--;
			} 
            else{
            	y[i+1]++;
			}
        }
        int l=0,r=n,answer=-1;
        while(l<=r){                   
            int mid=(l+r)>>1;
            if(check(mid)) answer=mid,r=mid-1;
            else l=mid+1;
        }
        cout<<answer<<endl;
    }
}