文章目录
什么是数据校验
在数据的传输过程中,无论使用什么方法,都无法保证100%的传输正确率,总有发生错误的时候。数据校验就是通过对发送方持有的数据(也就是正确的数据)进行某种运算,对接收方收到的数据也进行同样的运算,并且比较这两个结果。如果结果不一样,肯定是传输过程中发生了错误;而在有的情况下,即使结果一样,也不能认为数据传输是正确的,存在多处错误但是导致校验结果没有变的可能。
个人认为,数据校验是利用了信息的映射方法,试图找到一个映射,让原序列改变的时候它的映射结果也发生改变。当然,如果要做到原序列改变结果一定改变,这表示校验值的信息量和原序列是一样的,就失去了校验的意义,因为一方面成本太高,相当于把原信息再发送一遍;另一方面如果信息量一样,出现错误的可能就一样,如果连校验值在传输中都发生了错误,就没有校验的必要了,肯定得不到正确结果。所以无论什么校验方法,都有可能存在检测不出来错误的情况,但是通过精确的设计算法,可以降低这种可能。
奇偶校验
1. 什么是奇偶校验码
英文为:Parity Check
跟前面提到过的CRC校验码一样,奇偶校验码也是一种校验码,它用来检测数据传输过程中是否发生错误,是众多校验码中最为简单的一种。
顾名思义,它有两种校验方法:奇校验和偶校验
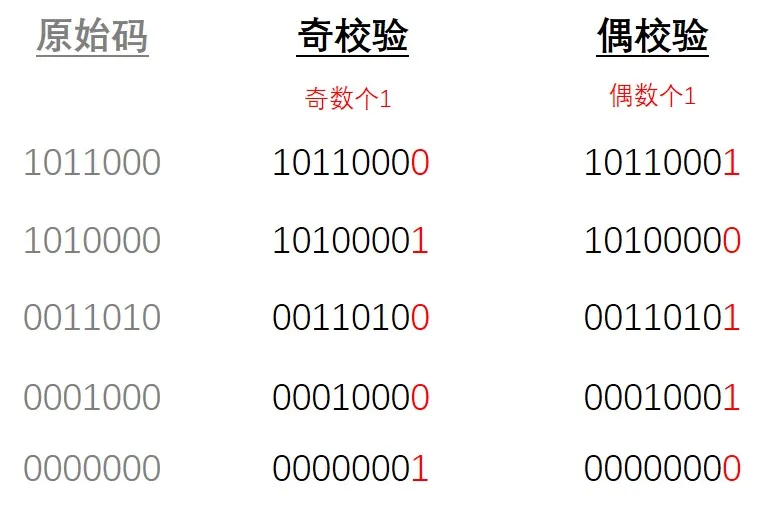
奇校验:原始码流+校验位 总共有奇数个1
偶校验:原始码流+校验位 总共有偶数个1
2. 算法
跟CRC类似,也是在原始码流后面,加上校验位。不同的是,它的校验位只有一位,要么是0,要么是1。并且它的校验码还可以放在码流的前面。
如下图。

例如下图有5组原始码,校验位的计算方法如下。红色代表校验位。
相信大家稍微动下脑子就能想明白,我就不做过多解释了。
3. 应用举例
奇偶校验码一个最为常见的应用场合就是ASCII码。
ASCII码占用一个字节,低7位是有效位,最高位用作奇偶校验。

4. 错误检测能力
只能检测出奇数个错误。
例如还是ASCII码 大写字母 A
奇校验 正确码流 11000001
错1位 11000011 变成了偶数个1,能检测出错误
错2位 11000010 变成了奇数个1,检测不出错误
错3位 11001010 变成了偶数个1,能检测出错误
偶校验 正确码流 01000001
错1位 01000011 变成了奇数个1,能检测出错误
错2位 01000010 变成了偶数个1,检测不出错误
错3位 01001010 变成了奇数个1,能检测出错误
5. 奇校验还是偶校验
那么使用中是选择奇校验还是偶校验呢? 其实都有应用了。
奇校验一个重要的特征是产生不了全0代码,所以在实际操作过程中选择的时候要考虑到这一点。
奇偶校验
奇偶校验(Parity Check)是最基础的校验方式,一般用在噪声低或者资源紧缺,而且重发成本不高的地方。
基本算法
奇偶校验的算法非常简单,就是统计数据中出现的1的个数,是奇数个还是偶数个。用软件编程语言可以简单的用比较和取反操作实现,而硬件描述语言则可以将输入信号简单地逐个异或运算。这里比较巧妙,证明如下:
对某一个序列,假设它具有奇性,那么它的奇偶位应该是1。这时在其后面添加0,则1和0异或还是1;如果添加1,那么1和1异或则变成了0。如果它具有偶性也同理,在后面添加0将不会改变其奇偶位,添加1则将变成具有奇性。再看初始情况,只有前两位是1和0异或能获得1,所以逻辑结果正确。
优点
奇偶校验的优点显而易见,就是它非常简单,对资源的消耗量也很低。很适合用在基础的地方,并且单个数据块比较小的地方,或者作为复杂校验协议的基础检查,降低之后的工作量。
缺点
奇偶校验的缺点也相当明显……首先是如果错码是偶数个,比如2个,奇偶校验就不会发现问题。虽然现在一般传输错码率比较低,但是在高噪声或者数据块很大(比如大文件)的情况下还是比较容易出现这种问题的。其次,奇偶校验只能提供基本的反馈:数据有错码,并不能知道具体哪一位出错,所以导致整个数据包被丢弃。
改进
对于简单的单向奇偶校验的基本改进就是双向奇偶校验。双向奇偶校验是对数据块进行的校验。考虑这样一种情况,我要传输一定的数据,按8位一字节传输。我可以使用:
1001010+1
这样的7+1格式,最后一位是校验码。但是如上文所说,有诸多限制,可以按这样的格式改进:
1001010+1
1011100+0
0100100+0
0011101+0
0101100+1
1011111+0
0111000+1
+
1100100 1
7字节一组,第8字节是前7字节的纵向奇偶校验。这样除非横纵同时仅出现偶数位错码才可能导致校验失效,概率非常低。值得一提的是,最后一位不仅是前7字节的校验位的校验,也是第8字节前7位的校验。这一位的存在属于双重冗余,能够进一步降低校验失败的可能。
纵向冗余校验
纵向冗余校验(Longitudinal Redundancy Check),也就是我们平时说的LRC,是对于单向奇偶校验的一个扩展。思路和奇偶校验是一样的,我这次研究的射频卡使用的主要就是LRC。
基本算法
LRC也是奇偶校验的形式,不同的是,它的方向是纵向的,也就是说它在获取全部的字节之后,把每个字节的第一位逐个异或生成校验字节的第一位,每个字节的第二位逐个异或生成校验字节的第二位,以此类推。
10010101
10111000
01001000
00111010
01011001
10111110
01110001
+
11001001
优点
LRC的优点是成本比奇偶校验更低,因为数据与校验的比例更大,所以传输的时候可以传输更多的数据和更少的校验值。在射频卡上使用也是这个原因,射频卡系统的资源非常有限,所以尽量采用低成本的方式。即使一般射频卡的噪声远大于常规有线传输,但是它的重发成本更低,后果也更轻,一次没有刷上大不了再刷一次,所以影响并不大。
缺点
LRC的缺点和单向奇偶校验一样,甚至更明显,因为它的数据与校验的比例更大,出现多重错码的概率更大。
整数加法校验和
整数加法校验和(Integer Addition Checksum),也就是最基本的Checksum算法,是很常用的校验方法。整数加法校验和也是一种纵向校验方法,生成一字节的校验码。
基本算法
整数加法校验和的基本算法非常简单,就是直接累加每个要传输的字节。全部累加之后,获得的结果就是校验码。需要注意的是,这里用的是正常的带进位加法,需要进位多少就正常进位。除了最高一位,进位被舍弃,因为校验码无论是由多少个字节生成的,都只有一字节长度。
优点
这一算法的优点是简单,因为是连续加法,所以并行运算也并不难做到,而且加法运算量本身不大,比较好实现。同时,Checksum方法不仅能够检出奇数个错码,还能检出2个错码(因为会由进位把错误传递到下一位),或其他更多的错码,除非错误被直接传递到了省略部分。
缺点
这一算法也有缺点,首先就是因为错误的上浮,不能知道究竟是哪里出现错码,也不能定位是第几个字节出现问题。同时,也存在错码被传递到被忽略部分,也就是最高位进上去的部分而不能检出错码的情况。
异或校验
【异或校验】与【校验和】类似,对数据进行“异或”,最终得到一个“异或值”。
uint8_t CheckXOR(uint8_t *Buf, uint8_t Len)
{
uint8_t i = 0;
uint8_t x = 0;
for(i=0; i<Len; i++)
{
x = x^(*(Buf+i));
}
return x;
}
校验和、异或校验的方式有很多种,比如有的还会传入一个参数作为异或校验的值。
当然,以上代码仅供学习参考,实际应用需结合项目情况修改代码。
CRC校验
已剪辑自: https://mp.weixin.qq.com/s/Dh9jwSo3GHGbM2MdHsk_-Q
一口君最近工作用到CRC校验,顺便整理本篇文章和大家一起研究。
1. 什么是CRC?
CRC(Cyclic Redundancy Checksum)是一种纠错技术,代表循环冗余校验和。
数据通信领域中最常用的一种差错校验码,其信息字段和校验字段长度可以任意指定,但要求通信双方定义的CRC标准一致。主要用来检测或校验数据传输或者保存后可能出现的错误。它的使用方式可以说明如下图所示:
在数据传输过程中,无论传输系统的设计再怎么完美,差错总会存在,这种差错可能会导致在链路上传输的一个或者多个帧被破坏(出现比特差错,0变为1,或者1变为0),从而接受方接收到错误的数据。
为尽量提高接受方收到数据的正确率,在接收方接收数据之前需要对数据进行差错检测,当且仅当检测的结果为正确时接收方才真正收下数据。检测的方式有多种,常见的有奇偶校验、因特网校验和循环冗余校验等。
2. 使用方法概述
循环冗余校验是一种用于校验通信链路上数字传输准确性的计算方法(通过某种数学运算来建立数据位和校验位的约定关系的 )。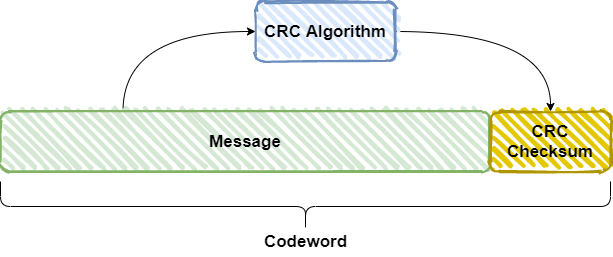
发送方计算机使用某公式计算出被传送数据所含信息的一个值,并将此值 附在被传送数据后,接收方计算机则对同一数据进行 相同的计算,应该得到相同的结果。
如果这两个 CRC结果不一致,则说明发送中出现了差错,接收方计算机可要求发送方计算机重新发送该数据。
3. 应用广泛
在诸多检错手段中,CRC是最著名的一种。CRC的全称是循环冗余校验,其特点是:检错能力强,开销小,易于用编码器及检测电路实现。从其检错能力来看,它所不能发现的错误的几率仅为0.0047%以下。
从性能上和开销上考虑,均远远优于奇偶校验及算术和校验等方式。
因而,在数据存储和数据通讯领域,CRC无处不在:著名的通讯协议X.25的FCS(帧检错序列)采用的是CRC-CCITT,WinRAR、NERO、ARJ、LHA等压缩工具软件采用的是CRC32,磁盘驱动器的读写采用了CRC16,通用的图像存储格式GIF、TIFF等也都用CRC作为检错手段。
这里需要知道几个组成部分或者说计算概念:多项式公式、多项式简记式、数据宽度、初始值、结果异或值、输入值反转、输出值反转、参数模型。
1、多项式公式
对于CRC标准除数,一般使用多项式(或二项式)公式表示,如下图中除数11011(poly值为0x1b)的二项式为G(X)=X4+X3+X+1,X的指数就代表了该bit位上的数据为1,(最低位为0)。
这里特别注意一下位数问题,除数的位数为二项式最高次幂+1(4+1=5),这个很重要。

2、多项式简记式
通过对CRC的基本了解我们知道,多项式的首尾必定为1,而这个1的位置在下一步计算一定为0,所以就把前面这个1给省略掉了,出现了一个叫简记式的东西,如上例中除数11011的简记式为1011,很多看过CRC高级语言源码的人会知道,对于CRC_16标准下G(X)=X16+X15+X2+1(16#18005)的poly值实际上是8005,这里使用的就是简记式。后面会对这个用法做一个说明。
3、数据宽度
数据宽度指的就是CRC校验码的长度(二进制位数),知道了CRC的运算概念和多项式,就可以理解这个概念了,CRC长度始终要比除数位数少1,与简记式长度是一致的。
以上三个数据就是我们经常能够用到的基本数据
4、初始值与结果异或值
在一些标准中,规定了初始值,则数据在进行上述二项式运算之前,需要先将要计算的数据与初始值的最低字节进行异或,然后再与多项式进行计算。
而在结果异或值不为零的情况下,则需要将计算得到的CRC结果值再与结果异或值进行一次异或计算,得到的最终值才是我们需要的CRC校验码。
这里可以看出,初始值与结果值的位数要求与数据宽度一致。
5、输入值反转与输出值反转
输入值反转的意思是在计算之前先将二项式反转,然后再用得到的新值和数据进行计算。如对于G(X)=X16+X15+X2+1(16#18005),其正向值为1 1000 0000 0000 0101,反转值则为1010 0000 0000 0001 1
输出值反转则是将最终得到的CRC结果反转。
通常,输入值反转后的结果值也会是反转的,所以这两个选项一般是同向的,我们只有在在线CRC计算器中会看到自由选择正反转的情况存在。
虽然CRC可以任意定义二项式、数据长度等,但没有一个统一的标准的话,就会让整个计算变得非常的麻烦。但实际上,不同的厂家经常采用不同的标准算法,这里列出了一些国际常用的模型表:
名称多项式表示法应用举例
| CRC-8 | X8+X2+X+1 | 0X107 | |
| CRC-12 | X12+X11+X3+X2+X+1 | 0X180F | telecom systems |
| CRC-16 | X16+X15+X2+1 | 0X18005 | Bisync, Modbus, USB, ANSI X3.28, SIA DC-07, many others; also known as CRC-16 and CRC-16-ANSI |
| CRC-CCITT | X16+X12+X5+1 | 0X11021 | ISO HDLC, ITU X.25, V.34/V.41/V.42, PPP-FCS |
| CRC-32 | X32+X26+X23+X22+X16+X12+X11+X10+X8+X7+X5+X4+X2+X+1 | 0x104C11DB7 | ZIP, RAR, IEEE 802 LAN/FDDI, IEEE 1394, PPP-FCS |
| CRC-32C | X32+X28+X27+X26+X25+X23+X22+X20+X19+X18+X14+X13+X11+X10+X9+X8+X6+1 | 0x11EDC6F41 | iSCSI, SCTP, G.hn payload, SSE4.2, Btrfs, ext4, Ceph |
在学习CRC校验算法之前,先复习一下CRC会涉及的主要几个主要的算法。
1. 异或
异或,就是不同为1,相同为0,运算符号是^。
0^0 = 0
0^1 = 1
1^1 = 0
1^0 = 1
异或运算存在如下几个规律,需要了解。
0^x = x 即0 异或任何数等于任何数
1^x = ~x 即1异或任何数等于任何数取反
x^x = 0 即任何数与自己异或,结果为0
a ^ b = b ^ a 交换律
a ^ (b ^ c) = (a ^ b) ^c 结合律
2. 模2加法
模2加法相对于普通的算术加法,主要的区别在模2加法,不做进位处理。具体结果如下。0+0 = 0 0+1 = 1 1+1 = 0 1+0 = 1 我们发现模2加法的计算结果,同异或运算结果一模一样。进一步推演,我们会发现,异或运算的5个规律,同样适合于模2加法。这里,就不在一一列举了。
3. 模2减法
模2减法相对于普通的算术减法,主要的区别在模2减法,不做借位处理。具体结果如下。0-0 = 0 0-1 = 1 1-1 = 0 1-0 = 1 我们发现模2减法的计算结果,同模2加法,以及异或的运算结果一模一样。进一步推演,我们会发现,异或运算的5个规律,同样适合于模2减法。这里,就不在一一列举了。
4. 模2除法
模2除法相对于普通的算术除法,主要的区别在模2除法,它既不向上位借位,也不比较除数和被除数的相同位数值的大小,只要以相同位数进行相除即可。
CRC原理:在K位信息码(目标发送数据)后再拼接R位校验码,使整个编码长度为N位,因此这种编码也叫(N,K)码。
通俗的说,就是在需要发送的信息后面附加一个数(即校验码),生成一个新的发送数据发送给接收端。这个数据要求能够使生成的新数据被一个特定的数整除。这里的整除需要引入模 2除法的概念。
那么,CRC校验的具体做法就是
(1)选定一个标准除数(K位二进制数据串)
(2)在要发送的数据(m位)后面加上K-1位0,然后将这个新数(M+K-1位)以模2除法的方式除以上面这个标准除数,所得到的余数也就是该数据的CRC校验码(注:余数必须比除数少且只少一位,不够就补0)
(3)将这个校验码附在原m位数据后面,构成新的M+K-1位数据,发送给接收端。
(4)接收端将接收到的数据除以标准除数,如果余数为0则认为数据正确。
注意:CRC校验中有两个关键点:
一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串(或多项式);
二是把原始帧与上面选定的除进行二进制除法运算,计算出FCS。
前者可以随机选择,也可按国际上通行的标准选择,但最高位和最低位必须均为“1”
实例:
由于CRC-32、CRC-16、CCITT和CRC-4的编码过程基本一致,只有位数和生成多项式不一样,下面就举例,来说明CRC校验码生成过程。
对于数据1110 0101(16#E5),以指定除数11011求它的CRC校验码,其过程如下:
使用上面计算的校验和和消息数据,可以创建要传输的码字。

有时候,我们需要填充checksum到制定的位置,这就涉及到字节序问题,建议用memcpy()进行拷贝。
实现算法参考网络相关代码,进行整理并验证,可直接使用。crc.c
/*
*一口Linux
*2021.6.21
*version: 1.0.0
*/
#include "crc.h"
#include <stdio.h>
typedef enum {
REF_4BIT = 4,
REF_5BIT = 5,
REF_6BIT = 6,
REF_7BIT = 7,
REF_8BIT = 8,
REF_16BIT = 16,
REF_32BIT = 32
}REFLECTED_MODE;
uint32_t ReflectedData(uint32_t data, REFLECTED_MODE mode)
{
data = ((data & 0xffff0000) >> 16) | ((data & 0x0000ffff) << 16);
data = ((data & 0xff00ff00) >> 8) | ((data & 0x00ff00ff) << 8);
data = ((data & 0xf0f0f0f0) >> 4) | ((data & 0x0f0f0f0f) << 4);
data = ((data & 0xcccccccc) >> 2) | ((data & 0x33333333) << 2);
data = ((data & 0xaaaaaaaa) >> 1) | ((data & 0x55555555) << 1);
switch (mode)
{
case REF_32BIT:
return data;
case REF_16BIT:
return (data >> 16) & 0xffff;
case REF_8BIT:
return (data >> 24) & 0xff;
case REF_7BIT:
return (data >> 25) & 0x7f;
case REF_6BIT:
return (data >> 26) & 0x7f;
case REF_5BIT:
return (data >> 27) & 0x1f;
case REF_4BIT:
return (data >> 28) & 0x0f;
}
return 0;
}
uint8_t CheckCrc4(uint8_t poly, uint8_t init, bool refIn, bool refOut, uint8_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint8_t i;
uint8_t crc;
if (refIn == true)
{
crc = init;
poly = ReflectedData(poly, REF_4BIT);
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x01)
{
crc >>= 1;
crc ^= poly;
}
else
{
crc >>= 1;
}
}
}
return crc ^ xorOut;
}
else
{
crc = init << 4;
poly <<= 4;
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x80)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
return (crc >> 4) ^ xorOut;
}
}
uint8_t CheckCrc5(uint8_t poly, uint8_t init, bool refIn, bool refOut, uint8_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint8_t i;
uint8_t crc;
if (refIn == true)
{
crc = init;
poly = ReflectedData(poly, REF_5BIT);
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x01)
{
crc >>= 1;
crc ^= poly;
}
else
{
crc >>= 1;
}
}
}
return crc ^ xorOut;
}
else
{
crc = init << 3;
poly <<= 3;
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x80)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
return (crc >> 3) ^ xorOut;
}
}
uint8_t CheckCrc6(uint8_t poly, uint8_t init, bool refIn, bool refOut, uint8_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint8_t i;
uint8_t crc;
if (refIn == true)
{
crc = init;
poly = ReflectedData(poly, REF_6BIT);
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x01)
{
crc >>= 1;
crc ^= poly;
}
else
{
crc >>= 1;
}
}
}
return crc ^ xorOut;
}
else
{
crc = init << 2;
poly <<= 2;
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x80)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
return (crc >> 2) ^ xorOut;
}
}
uint8_t CheckCrc7(uint8_t poly, uint8_t init, bool refIn, bool refOut, uint8_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint8_t i;
uint8_t crc;
if (refIn == true)
{
crc = init;
poly = ReflectedData(poly, REF_7BIT);
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x01)
{
crc >>= 1;
crc ^= poly;
}
else
{
crc >>= 1;
}
}
}
return crc ^ xorOut;
}
else
{
crc = init << 1;
poly <<= 1;
while (length--)
{
crc ^= *buffer++;
for (i = 0; i < 8; i++)
{
if (crc & 0x80)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
return (crc >> 1) ^ xorOut;
}
}
uint8_t CheckCrc8(uint8_t poly, uint8_t init, bool refIn, bool refOut, uint8_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint32_t i = 0;
uint8_t crc = init;
while (length--)
{
if (refIn == true)
{
crc ^= ReflectedData(*buffer++, REF_8BIT);
}
else
{
crc ^= *buffer++;
}
for (i = 0; i < 8; i++)
{
if (crc & 0x80)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
if (refOut == true)
{
crc = ReflectedData(crc, REF_8BIT);
}
return crc ^ xorOut;
}
uint16_t CheckCrc16(uint16_t poly, uint16_t init, bool refIn, bool refOut, uint16_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint32_t i = 0;
uint16_t crc = init;
while (length--)
{
if (refIn == true)
{
crc ^= ReflectedData(*buffer++, REF_8BIT) << 8;
}
else
{
crc ^= (*buffer++) << 8;
}
for (i = 0; i < 8; i++)
{
if (crc & 0x8000)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
if (refOut == true)
{
crc = ReflectedData(crc, REF_16BIT);
}
return crc ^ xorOut;
}
uint32_t CheckCrc32(uint32_t poly, uint32_t init, bool refIn, bool refOut, uint32_t xorOut,
const uint8_t *buffer, uint32_t length)
{
uint32_t i = 0;
uint32_t crc = init;
while (length--)
{
if (refIn == true)
{
crc ^= ReflectedData(*buffer++, REF_8BIT) << 24;
}
else
{
crc ^= (*buffer++) << 24;
}
for (i = 0; i < 8; i++)
{
if (crc & 0x80000000)
{
crc <<= 1;
crc ^= poly;
}
else
{
crc <<= 1;
}
}
}
if (refOut == true)
{
crc = ReflectedData(crc, REF_32BIT);
}
return crc ^ xorOut;
}
uint32_t CrcCheck(CRC_Type crcType, const uint8_t *buffer, uint32_t length)
{
switch (crcType.width)
{
case 4:
return CheckCrc4(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 5:
return CheckCrc5(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 6:
return CheckCrc6(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 7:
return CheckCrc7(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 8:
return CheckCrc8(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 16:
return CheckCrc16(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
case 32:
return CheckCrc32(crcType.poly, crcType.init, crcType.refIn, crcType.refOut,
crcType.xorOut, buffer, length);
}
return 0;
}
crc.h
/*
*一口Linux
*2021.6.21
*version: 1.0.0
*/
#ifndef __CRC_H__
#define __CRC_H__
#include <stdint.h>
#include <stdbool.h>
typedef struct {
uint8_t width;
uint32_t poly;
uint32_t init;
bool refIn;
bool refOut;
uint32_t xorOut;
}CRC_Type;
uint32_t CrcCheck(CRC_Type crcType, const uint8_t *buffer, uint32_t length);
#endif
main.c
/*
*一口Linux
*2021.6.21
*version: 1.0.0
*/
#include <stdio.h>
#include <stdint.h>
#include <stdbool.h>
#include "crc.h"
#define LENGTH 8
const uint8_t data[3][LENGTH] = {
{ 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08 },
{ 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80 },
{ 0xfe, 0xfd, 0xfb, 0xf7, 0xef, 0xdf, 0xbf, 0x7f }};
typedef struct {
CRC_Type crcType;
uint32_t result[3];
}CRC_Test;
CRC_Test crc4_ITU = { { 4, 0x03, 0x00, true, true, 0x00 }, { 0x0f, 0x0a, 0x0e } };
CRC_Test crc5_EPC = { { 5, 0x09, 0x09, false, false, 0x00 }, { 0x00, 0x0c, 0x17 } };
CRC_Test crc5_ITU = { { 5, 0x15, 0x00, true, true, 0x00 }, { 0x16, 0x0a, 0x17 } };
CRC_Test crc5_USB = { { 5, 0x05, 0x1f, true, true, 0x1f }, { 0x10, 0x09, 0x17 } };
CRC_Test crc6_ITU = { { 6, 0x03, 0x00, true, true, 0x00 }, { 0x1d, 0x30, 0x00 } };
CRC_Test crc7_MMC = { { 7, 0x09, 0x00, false, false, 0x00 }, { 0x57, 0x30, 0x5b } };
CRC_Test crc8 = { { 8, 0x07, 0x00, false, false, 0x00 }, { 0x3e, 0xe1, 0x36 } };
CRC_Test crc8_ITU = { { 8, 0x07, 0x00, false, false, 0x55 }, { 0x6b, 0xb4, 0x63 } };
CRC_Test crc8_ROHC = { { 8, 0x07, 0xff, true, true, 0x00 }, { 0x6b, 0x78, 0x93 } };
CRC_Test crc8_MAXIM = { { 8, 0x31, 0x00, true, true, 0x00 }, { 0x83, 0x60, 0xa9 } };
CRC_Test crc16_IBM = { { 16, 0x8005, 0x0000, true, true, 0x0000 }, { 0xc4f0, 0x2337, 0xa776 } };
CRC_Test crc16_MAXIM = { { 16, 0x8005, 0x0000, true, true, 0xffff }, { 0x3b0f, 0xdcc8, 0x5889 } };
CRC_Test crc16_USB = { { 16, 0x8005, 0xffff, true, true, 0xffff }, { 0x304f, 0xd788, 0x53c9 } };
CRC_Test crc16_MODBUS = { { 16, 0x8005, 0xffff, true, true, 0x0000 }, { 0xcfb0, 0x2877, 0xac36 } };
CRC_Test crc16_CCITT = { { 16, 0x1021, 0x0000, true, true, 0x0000 }, { 0xeea7, 0xfe7c, 0x7919 } };
CRC_Test crc16_CCITT_FALSE = { { 16, 0x1021, 0xffff, false, false, 0x0000 }, { 0x4792, 0x13a7, 0xb546 } };
CRC_Test crc16_X25 = { { 16, 0x1021, 0xffff, true, true, 0xffff }, { 0x6dd5, 0x7d0f, 0xfa6a } };
CRC_Test crc16_XMODEM = { { 16, 0x1021, 0x0000, false, false, 0x0000 }, { 0x76ac, 0x2299, 0x8478 } };
CRC_Test crc16_DNP = { { 16, 0x3D65, 0x0000, true, true, 0xffff }, { 0x7bda, 0x0535, 0x08c4 } };
CRC_Test crc32 = { { 32, 0x04c11db7, 0xffffffff, true, true, 0xffffffff }, { 0x3fca88c5, 0xe0631a53, 0xa4051a26 } };
CRC_Test crc32_MPEG2 = { { 32, 0x4c11db7, 0xffffffff, false, false, 0x00000000 }, { 0x14dbbdd8, 0x6509b4b6, 0xcb09d294 } };
void CrcTest(CRC_Test crcTest)
{
uint32_t i;
for (i = 0; i < 3; i++)
{
printf("%08x\t%08x\r\n", CrcCheck(crcTest.crcType, data[i], LENGTH), crcTest.result[i]);
}
printf("\r\n");
}
int main(void)
{
CrcTest(crc4_ITU);
CrcTest(crc5_EPC);
CrcTest(crc5_ITU);
CrcTest(crc5_USB);
CrcTest(crc6_ITU);
CrcTest(crc7_MMC);
CrcTest(crc8);
CrcTest(crc8_ITU);
CrcTest(crc8_ROHC);
CrcTest(crc8_MAXIM);
CrcTest(crc16_IBM);
CrcTest(crc16_MAXIM);
CrcTest(crc16_USB);
CrcTest(crc16_MODBUS);
CrcTest(crc16_CCITT);
CrcTest(crc16_CCITT_FALSE);
CrcTest(crc16_X25);
CrcTest(crc16_XMODEM);
CrcTest(crc16_DNP);
CrcTest(crc32);
CrcTest(crc32_MPEG2);
return 0;
}
注意
不同的CRC算法,对00H或FFH数据流的计算结果不一样,部分算法存在校验结果也为00H或FFH的情况(也就意味着存储空间处于初始化状态时:全0或全1,CRC校验反而是正确的),在应用中需要注意避免。
原文来源于:一口linux
版权归原作者或平台所有,仅供学习参考与学术研究,如有侵权,麻烦联系删除~感谢
最 后
小哥搜集了一些嵌入式学习资料,公众号内回复【1024】即可找到下载链接!
推荐好文 点击蓝色字体即可跳转☞ 专辑|Linux应用程序编程大全☞ 专辑|学点网络知识☞ 专辑|手撕C语言
☞ 专辑|手撕C++语言☞ 专辑|经验分享☞ 专辑|从单片机到Linux☞ 专辑|电能控制技术☞ MCU进阶专辑 ☞ 嵌入式C语言进阶专辑 ☞ 经验分享
md5
相对于之前介绍的校验方法,md5复杂很多。md5(MD5 Message-Digest Algorithm)是一种信息摘要算法,它能够对任意长度的信息生成128位的摘要,抗碰撞性能比较强,主要用在对于校验和防篡改要求比较高的地方。
基本算法
鉴于md5算法的复杂性,在这里就不完全展开讲解了,只解释基本而必要的部分。
首先,md5算法对512位一块的数据进行处理,所以首先要对数据位数进行填充。如果数据长度模512之后不是448,那么就填充一个1和多个0,直到填充至模512之后是448。为什么是448?因为算法使用一个64位的数字来存放填充前的数据长度,这64位将跟在填充后的数据的最后面,这样448+64=512,完成之后正好是512的倍数。
其次,在md5算法中存在幻数的概念。幻数(就是数论里的那个幻数)使用的是标准32位幻数,也就是0123456789ABCDEFFEDCBA9876543210,被分成4组,每组8位按照物理顺序放在寄存器内部(所以根据处理器架构的不同,程序中这个数字可能需要改)。
之后将每个512位的分组数据分成16个32位的部分,对每一部分使用四个标准线性函数进行运算,数据被分成几组就循环几次。
Misplaced &Misplaced &
Misplaced &Misplaced &
Double exponent: use braces to clarifyDouble exponent: use braces to clarify
I(X,Y,Z)=Y(X|( Z))
在经过一定的运算,每次循环分开使用四个不同的函数之后,将获得md5的校验值,128位。
优点
md5的最大的优点就是它的防碰撞能力很强,正常情况下,不人为干预而传输错误导致md5值一样是不可能的,所以一定能够检出传输错误。同时,鉴于它的防碰撞能力很强,也被用来进行脱敏存储,比如数据库中存放的用户密码,或者Windows10离线账户的登陆密码就是以md5形式保存的,避免有人能够直接看到密码。而因为信息在进行摘要的过程中存在损失,所以是不可能精确还原回原来的信息的,再加上对md5没有办法进行逆运算,只能暴力试验,所以一定程度上防止了密码泄露。md5被广泛用在类似的安全认证方面和文件特别是大文件的校验上。
缺点
md5同时也有自己的缺点。首先md5并非理论上防碰撞,只是碰撞率很低,所以通过一定的方法还是可以找到一个序列,md5值和已知的相等。虽然没有办法还原原来的信息,但是对于密码认证方面却非常有效,因为毕竟只验证md5,所以只要能对上,就能通过。所以安全性很高的地方和数字签名方面不能使用md5。另一方面md5验证过程比较复杂,没有硬件实现(因为成本太高了),对于流量很高的系统是一个挑战。
破解
严格来说这一节讲的不是md5的破解而是碰撞,但是鉴于大多数人好像习惯于叫破解,还是沿用这一称呼。
上文中讲到md5可以用特殊的手段在合理的时间内碰撞成功,现在通行的手段就是彩虹表。彩虹表是一种特殊方式生成的查找表,利用的是暴力破解结合查找表的方式对md5进行碰撞。彩虹表使用相关衰减函数代替原来的顺序排列衰减函数,同时特殊排列其顺序,因为如果两个md5值碰撞,在散列链中一定出现在同样的位置并从此重合。所以通过保存哈希链,结合暴力破解(反算和正算)和查找表,允许通过定位哈希链的起点和终点而在运行破解的时候降低碰撞运算次数。
可以想到,这个表越大,那么需要计算和定位逆向初始位置的时间就越短,覆盖面也尽可能地大,但是存储的空间代价越大,目前经过大家的收集和整理,最大的彩虹表接近120G;而用很小的彩虹表也可以达到目标,但是定位的时间会长很多,错误概率也会增加,而定位错误将导致这次运行无法获得需要的结果。目前基本彩虹表大约380M,基础的彩虹表破解工具内置的就是这个彩虹表。
至于具体怎么利用彩虹表破解各种认证,针对不同的情况和不同的工具操作并不一样。这一块在以后的文章中进行讨论。根据我个人对经验来看,大容量彩虹表不一定能够很大的提高破解速度,反而能够提高成功率,换用120G彩虹表之后之前碰撞不出来的Windows离线账户密码可以成功,网上还有专门的md5碰撞服务,我没有试过,不过根据他们自己的描述,应该是比自己运行小规模彩虹表效果好很多。
 常见数据校验算法介绍
常见数据校验算法介绍
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










